Грунты учебник

Рис. 12. Схема прибора для испытания грунтов на сдвиг

1- образец грунта естественного сложения;

2- стандартное кольцо;

3- пористая пластина;

4- пористый штамп;

5- фильтровальная бумага;

6- шарнир;

7- подвижная каретка;

8- зажимы верхней части кольца;

9- индикатор для измерения осадки штампа при увеличении нагрузки; 10 - индикатор для измерения деформаций сдвига.

Предусматривается проведение трёх испытаний при различных вертикальных давлениях на образец грунта: Р = 100 – 200 – 300 кПа.

При каждом из этих вертикальных давлений определяют величину сдвигающей горизонтальной силы и соответствующее горизонтальное

20

В результате строятся графики сдвига (рис. 13,14).

Для песчаного грунта – график сдвига отвечает закону Кулона τ = ptg и читается: «Сопротивление песчаного грунта сдвигу есть сопротивление трению, которое пропорционально вертикальному давлению».

Для глинистого грунта – закон Кулона выражается τ = ptgφ + C и читается: «Сопротивление грунта сдвигу складывается из сопротивлению трению, которое пропорционально вертикальному давлению и силы удельного сцепления, которое не зависит от вертикального давления».

По графикам определяются значения φ и C.

σƐ – давление всесторонних сил связности, определяемое по формуле:

σO = Q PR = C · ctgφ.

Примечание:

1.Самостоятельно ознакомиться в учебниках:

-с испытаниями грунта на трехосное сжатие в стабилометре;

-с определением коэффициента бокового расширения µ и коэффициентом бокового давления ξ.

2.В геотехнической лаборатории выполнить работы по определению физических и механических характеристик грунтов.

3.При выполнении расчетно-практических работ, курсовых и дипломных проектов применить полученные знания.

21

2. ТЕОРИЯ РАСПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ В ГРУНТЕ

Для проведения расчетов оснований и фундаментов по деформациям необходимо знать законы распределения напряжений в грунтовом массиве.

В этом случае используются положения теории упругости при соблюдении следующих ограничений:

напряжения рассматриваются только напряжения в расчетах принимаются при прямолинейной зависимости при завершенной осадке

S=f(P)

в) грунт рассматривается однородным и изотропным, характеризующимся Е и ʋ.

Рассматриваемые в этом разделе позиции являются важнейшими для установления закономерности формирования НДЗ (напряженнодеформируемой зоны).

Рассматриваются 2 задачи: пространственная и плоская.

2.1. Распределение напряжений в случае пространственной задачи

2.1.1. Сосредоточенная сила приложена на поверхности линейно - деформируемого полупространства

Решение дано Буссинеском и позволяет определить все составляющие напряжений: σх, σy, σz, τхy, τхz, τyz, и перемещения: Wх, Wy, Wz.

Врезультате решения задачи

Буссинеском получено:

σT = K · V8>,

где К – табличный коэффициент; z – глубина заложения точки М.

Рис. 15. Схема к определению напряжений от действия сосредоточенной силы

22

2.1.2. Система сосредоточенных сил

При решении этой задачи используется решение Буссинеска и принцип

независимого действия сил:

σT = K 8V>== + K4 8V>>> + KW 8V>XX.

Рис. 16. Схема к определению напряжений от действия нескольких сосредоточенных сил

2.1.3. Действие равномерно распределенной нагрузки, приложенной

впределах прямоугольного контура

Вэтом случае выделяется элементарная площадка dF, в которой нагрузка представляется в виде сосредоточенной силы. Интегрируя по всей площадке, получают значение σz. Однако решение сложное и в практических расчётах не применяется.

Рис. 17. Схема к определению напряжения от действия равномерно распределённой нагрузки в пределах прямоугольного контура

Ученый Лавэ развил это решение до табличных значений в определении напряжений под центром загрузки σT< = α<P и в определении напряжений под углами загрузки σT = α P, где αо и αс – табличные коэффициенты.

2.1.4. Метод угловых точек для определения σz

Выделяют три случая (рис. 18):

а) точка М внутри контура загрузки. В этом случае загрузка делится на 2, тогда σT = α + α 4 · P;

б) точка М внутри контура загрузки. В этом случае

загрузка делится на 4 прямоугольника с углами в точке М, тогда σT = α + α 4 + α W + α Z · P;

23

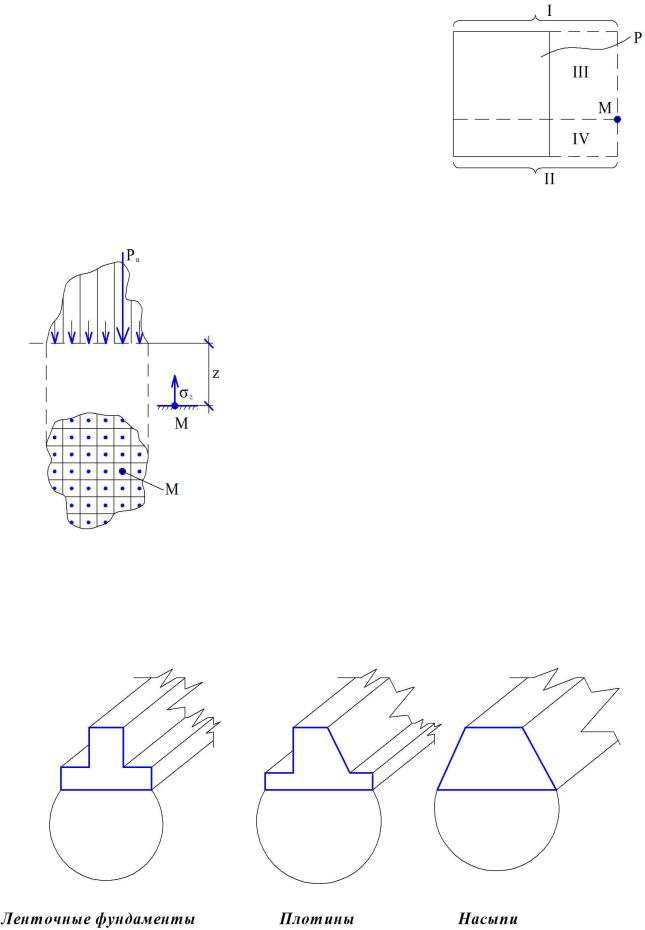
в) точка М вне контура загрузки. В этом случае достраивается прямоугольник и разбивается

на составляющие в соответствии со схемой,

тогда σT = α + α 4 − α W − α Z · P.

Рис. 18. Схема к определению напряжений методом угловых точек

2.1.5. Метод элементарного суммирования

Рассматривается задача определения σz в точке М от нагрузки, любым образом распределенной в плане и любой интенсивности.

В этом случае нагрузка делится на элементарные площадки. В каждой из них нагрузка представляется в виде сосредоточенной силы и, используя решение Буссинеска, определяется σz, в точке М как сумма напряжений от

действия сосредоточенных сил.

σT = ∑]\^ K\ V8>_ .

Рис. 19. Схема к определению напряжений методом элементарного суммирования

2.2.Распределение напряжений в случае плоской задачи

Впрактике строительства часто встречаются случаи по проектированию протяжённых по длине фундаментов.

24

Во всех этих случаях напряжённо-деформированная зона в одном поперечном сечении сооружения будет аналогична и для других сечений, выбранных по длине, поэтому решение сводится к плоской задаче.

Рис. 20. Схема к определению напряжений от действия сосредоточенной силы (решение Фломана)

2.2.2. Определение составляющих напряжений от действия полосообразной нагрузки, любым образом распределённой по ширине фундамента

Согласно схеме положение точки М относительно нагрузки определяется углами β1 и β2 и глубиной заложения z. При решении

выделяется элементарный участок dy, в нем нагрузка представляется сосредоточенной силой. Используя решение Фломана и интегрируя по всей ширине b, получим:

σT = 4 dA> Руsin4 βdβ

` A= ,

σc = 4 dA> Руcos4 βdβ

4 `A A= ,

τ = ` dA=> Руsin βcosβdβ.

Рис. 21. Схема к определению составляющих напряжений от действия полосообразной нагрузки, любым способом распределённой по ширине

25

Даются и частные решения:

−для треугольной нагрузки,

−для трапециевидной нагрузки,

−для прямоугольной нагрузки.

2.2.3.Распределение напряжений от действия полосообразной равномерно-распределённой нагрузки

Аналогично выше рассмотренной задаче, Фломан довёл решение до табличных значений, согласно которым:

Рис. 22. Схема к определению составляющих напряжений от действия полосообразной равномерно распределенной нагрузки

Эпюры вертикальных, горизонтальных и касательных напряжений σz, σy, τ

На рис. 23 и 24 представлены эти эпюры, из рассмотрения которых можно сделать следующие выводы:

1.Напряжения в основании фундаментов распределяются на значительную глубину (до 6в).

2.Основная концентрация напряжений захватывает зону на глубину под подошвой фундамента до 2в.

3.В проектной практике при расчёте осадки принимается эпюра

распределения вертикальных напряжений σz под центром фундамента в виде «дамского каблучка» (рис. 23а).

4.При рассмотрении эпюр σу τ также подтверждается, что основная концентрация напряжений происходит в слое под подошвой фундамента, глубиной до 2в.

По эпюре τ видно, что зоны предельного равновесия грунта образуются под краями фундаментов, где грунт становится подобен вязкой жидкости и стремится выйти из-под подошвы фундамента.

26

Рис. 23. Эпюры распределения сжимающих напряжений σz по вертикальным (а) и горизонтальным (б) сечениям массива грунта

Рис. 24. Линии равных напряжений в линейно деформируемом массиве в случае плоской задачи:

а-изобары σz; б-распоры σу; в-сдвиги τzx

27

2.3. Распределение напряжений при наличии жёсткого подстилающего слоя

В практике проектирования рассматриваются и случаи, когда на глубине залегает практически не сжимающийся слой. Он рассматривается как

жёсткий подстилающий слой.

Установлено, что при наличии на глубине жёсткого подстилающего слоя происходит концентрация напряжений, что видно на рис. 25, где:

1 – эпюра σz при однородном основании;

2 – эпюра σz при наличии жёсткого подстилающего слоя на глубине b, 2b, 5b.

Решение для построения этих эпюр дано профессором Егоровым К.Е.

σ на любой глубине определяется по формулеz σT = αP, где α – коэффициент уменьшения Р с глубиной с учётом наличия жёсткого подстилающего слоя.

В учебниках [1, 2] даны таблицы профессора Егорова К.Е. для круглых и квадратных фундаментов и профессора Горбунова – Посадова для прямоугольных и ленточных фундаментов.

Рис. 25 Схема к определению напряжений при наличии жёсткого подстилающего слоя

2.4. Фактические и расчётные эпюры контактных напряжений

Рис. 26. Эпюры контактны напряжений

28

В проектной практике используются эпюры контактных напряжений на опорной площади фундаментов осреднённой прямоугольной формы – Рср. (рис. 26).

Однако экспериментальными работами установлено, что фактические эпюры имеют следующий вид:

−колокообразные – при фундаментах малых размеров, больших нагрузках и мало сжимаемых грунтах;

−седлообразные – при фундаментах больших размеров, малых давлениях и сильно сжимаемых грунтах;

−параболические – при промежуточных значениях.

При проектировании ответственных сооружений расчёт фундаментов по прочности следует производить с учётом фактических эпюр контактных напряжений.

3. ТЕОРИЯ ПРЕДЕЛЬНОГО НАПРЯЖЁННОГО СОСТОЯНИЯ ГРУНТОВ

3.1. Фазы напряжённого состояния грунта. Критические нагрузки на грунты основания

На графике (рис. 27) испытания грунта штампом отражается зависимость S=f(P).

Выделяются 3 фазы:

1– фаза уплотнения;

2– фаза сдвигов;

3– фаза выпирания.

На графике выделяются две критические нагрузки на грунт:

Рн.кр. – начальная критическая нагрузка на грунт (соответствует конечной точке прямолинейного участка графика); Рпр. – предельная нагрузка на грунт.

Рис. 27. График зависимости S=f(P) фазы напряжённого состояния грунта

Рассмотрим поведение грунтов в этих фазах, которое иллюстрируется рис. 28.

29