5
Исключая t в уравнениях (1.1) и (1.2), получим уравнение траектории движения материальной точки. Траектория движения материальной точки — линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным.
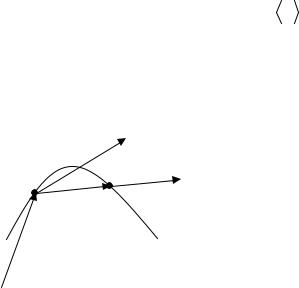
Рассмотрим движение материальной точки вдоль произвольной траектории (рис. 2). Отсчет времени начнем с момента, когда точка находилась в положении А. Длина участка траектории АВ, пройденного материальной
точкой с момента начала отсчета времени, называется длиной пути |
s |
и |
|
является скалярной функцией |
времени: s = s (t). Вектор г = г |
— |
г0, |
проведенный из начального положения движущейся точки в положение ее в |
|||
данный момент времени, называется перемещением. |
|
|
|
Естественно, что при прямолинейном движении вектор перемещения |
|||
совпадает с соответствующим |
участком траектории и модуль перемещения |
||
| г | равен пройденному пути |
s. |
|
|
§ 2. Скорость
Для характеристики движения материальной точки вводится векторная величина — скорость, которая определяет как быстроту движения, так и его направление в данный момент времени. Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус-вектор r0 (рис. 3). В течение небольшого промежутка времени t точка пройдет путь s и получит элементарное перемещение r.
Величина
|
|
|
v |
= |
∆r |
|
|
|
(2.1) |
|
|
|
|
|
|
∆t |
|
|
|
|
|
называется средней скоростью движения за время |
t. Направление средней |
|||||||||
|
|
|
скорости |
совпадает |
с направлением |
г. |
||||
|
v |
|
Если |
в |
(2.1) |
перейти |
к пределу |
при |
||
|
|
г → 0, то |
получим |
выражение |
для |
|||||
|
s |
<v> |
мгновенной скорости v: |
|
|
|
||||
A |
|
|
|
|
|
|
|
|
||
B |
|
|
|
|
|
∆r |
= dr |
|
|
|
|
r |
|
|
|
v = lim |
|
|
|||
|
|
|
|
|
|
∆r →0 |
∆t |
dt |
|
|
r0 |
|
|
|
Мгновенная |
скорость |
v |
есть |
|||
0 |
|
|
векторная величина, |
равная |
первой |
|||||
|
Рис. 3 |
|
производной |
|
|
радиуса-вектора |
||||
|
|
|
движущейся точки по времени. Так как |
|||||||
|
|
|
секущая |
в |
пределе |
совпадает |
с |
|||
касательной, то вектор скорости v направлен по касательной к траектории в сторону движения (рис. 3).
6
По мере уменьшения t путь |
s все больше будет приближаться к | r |, |
|||||||||
поэтому |
|
|
|
|
|
|
|
|
|
|
|
∆r |
|
|
|
|∆r | |
|
∆s |
= ds |
||
υ =| v |= |
lim |
|
= lim |
= lim |
||||||
∆t |
|
|
∆t |
|
∆t |
|||||
|
∆r →0 |
|
|
∆r →0 |
∆r →0 |
dt |
||||
Таким образом, числовое значение мгновенной скорости равно первой производной пути по времени:
υ= lim |
∆s |
= ds |
(2.2) |
∆r→0 |
∆t |
dt |
|
В случае неравномерного движения, когда числовое значение мгновенной скорости с течением времени изменяется, пользуются скалярной величиной <v> – средней скоростью неравномерного движения на данном участке:
υ = |
∆s |
|
∆t |
Из рис. 3 вытекает, что <v> > | <v> |, так как s > | г | и только в случае |
|
прямолинейного движения |
|
Δs = | |
г | |
Если выражение ds υ= dt см( . формулу (2.2)) проинтегрировать по временив пределах от t до t + t, то найдем длину пути, пройденного точкой за время t:
t+∆t |
|
s = ∫υ dt |
(2.3) |
t
В случае равномерного движения, когда числовое значение мгновенной скорости постоянно, выражение (2.3) примет вид
t+∆t
s = υ ∫dt = υ ∆t
t
Путь, пройденный точкой за промежуток времени от t1 до t2, дается интегралом
t2
s = ∫υ(t) dt
t1