
- •Содержание
- •Введение
- •1 Анализ исследований повреждения материалов в результате процессов усталости и ползучести
- •2 Уравнения математических моделей термовязкопластичности и накопления повреждений по [13]
- •2.1 Уравнения термовязкопластичности
- •2.2 Уравнения накопления повреждений
- •3 Исследование работы компенсаторов магистральных трубопроводов в программном комплексеScadOffice
- •4 Анализ работы компенсаторов магистральных трубопроводов в комплексе компьютерного инженерного анализаNxNastran
- •Список использованной литературы
2 Уравнения математических моделей термовязкопластичности и накопления повреждений по [13]
уравнения накопления повреждений, позволяющие учитывать: суммирование повреждений от различных механизмов деградации материала, двухстадийность и нелинейность процесса повреждения, нелинейность суммирования повреждений при блочных режимах циклического деформирования, зависимость скорости накопления повреждений от вида напряженного состояния и вида траектории деформаций.
2.1 Уравнения термовязкопластичности
Уравнения термовязкопластичности, позволяют описывать: эффект Баушингера, нелинейный характер монотонного и циклического упрочнения, эффекты стабилизации и циклической памяти материала, зависимость величины упрочнения от направления деформирования и от характера траектории деформаций.
Считая материал пластически несжимаемым, принимаем закон суммирования упругих и необратимых деформаций:
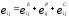 ,
,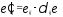 , (1,2)
, (1,2)
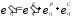 ,
,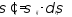 , (3,4)
, (3,4)
где
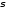 и
и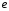 шаровые составляющие тензоров
напряжений и деформаций,
шаровые составляющие тензоров
напряжений и деформаций,
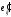 и
и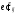 девиаторы тензоров полных и упругих
деформаций,
девиаторы тензоров полных и упругих
деформаций,
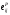 и
и тензоры пластических деформаций и
деформаций ползучести.
тензоры пластических деформаций и
деформаций ползучести.
Считаем справедливым также известный закон, связывающий напряжения с упругими деформациями:
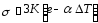 ,
,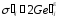 , (5,6)
, (5,6)
для которого
экспериментально определяются функции:
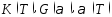 .
.
Примем следующее выражение для пластического потенциала:
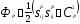 , где
, где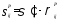 , (7,8)
, (7,8)
где 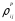 −
тензор микронапряжений, определяющий
положение центра поверхности текучести,
а
−
тензор микронапряжений, определяющий
положение центра поверхности текучести,
а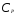 −
ее радиус.
−
ее радиус.
Из ассоциированного закона течения получим выражение для скорости пластических деформаций при активном нагружении:
 при
при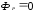 и
и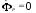 . (9)
. (9)
Закон изотропного упрочнения сформулируем в виде:
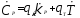 ,
,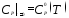 , (10)
, (10)
где 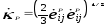 . (11)
. (11)
Для определения модуля изотропного
упрочнения
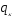 используем формулу:
используем формулу:
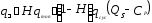 , (12)
, (12)
где
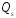 −
значение радиуса поверхности текучести
в ее стабильном состоянии,
−
значение радиуса поверхности текучести
в ее стабильном состоянии,
в соответствии
с которой
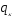 принимает либо значение
принимает либо значение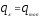 при монотонном деформировании, либо
при монотонном деформировании, либо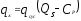 при циклическом деформировании. Для
переключения характера упрочнения
используется функция Хевисайда:
при циклическом деформировании. Для
переключения характера упрочнения
используется функция Хевисайда:
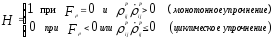 (13)
(13)
и поверхность
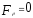 ,
где
,
где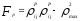 , (14)
, (14)
Длина траектории пластических деформаций при таком описании изотропного упрочнения естественным образом распадается на два участка: участок с монотонным упрочнением и участок с циклическим упрочнением:
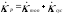 ,
,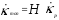 ,
,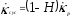 . (15)
. (15)
Кроме того, «поверхность памяти»
 позволяет сохранять информацию о
достигнутых циклически стабильных
состояниях материала и осуществлять
постепенное стирание этой информации
при переходе к циклическому деформированию
с меньшей амплитудой. Для этого
сформулировано следующее эволюционное
уравнение изменения ее радиуса:
позволяет сохранять информацию о
достигнутых циклически стабильных
состояниях материала и осуществлять
постепенное стирание этой информации
при переходе к циклическому деформированию
с меньшей амплитудой. Для этого
сформулировано следующее эволюционное
уравнение изменения ее радиуса:
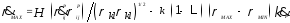 , (16)
, (16)
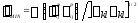 , (17)
, (17)
где 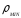 − значение
− значение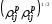 в
момент смены знака произведения
в
момент смены знака произведения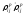 ,
а
,
а
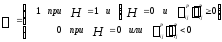 . (18)
. (18)
Модуль монотонного упрочнения
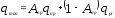 (19)
(19)
и значение, к которому стремится радиус поверхности текучести в процессе циклического упрочнения
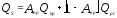 , (20)
, (20)
приняты
зависящими от параметра, характеризующего
степень непропорциональности процесса
деформирования. BenallalиMarquisпредложили вычислять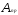 следующим
образом:
следующим
образом:
 , (21)
, (21)
где
 −
численная характеристика степени
несоосности каких-либо двух тензоров,
определяющих кинетику
напряженно-деформированного состояния.
−
численная характеристика степени
несоосности каких-либо двух тензоров,
определяющих кинетику
напряженно-деформированного состояния.
С помощью эксперимента должны определяться следующие функции:
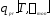 ,
,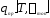 ,
,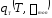 ,
,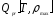 ,
,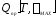 ,
,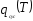 .
.
Закон кинематического упрочнения принят в виде:
 , (22)
, (22)
где 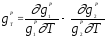 . (23)
. (23)
С помощью эксперимента должны определяться следующие функции:
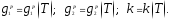
Постулируя существование потенциала ползучести в виде:
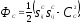 , где
, где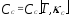 , (24)
, (24)
принимаем следующее правило определения скорости деформаций ползучести:
 ,
где
,
где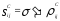 , (25)
, (25)
где 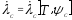 при
при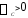 и
и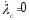 при
при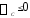 , (25)
, (25)
 . (26)
. (26)
По аналогии с законом кинематического упрочнения, эволюционное уравнение, определяющее смещение центров эквипотенциальных поверхностей ползучести, принято в следующем виде:
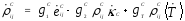 (28)
(28)
где
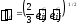 ,
,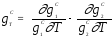 .
(29,30)
.
(29,30)
С помощью эксперимента должны определяться следующие функции:
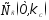 ,
,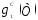 ,
,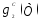 ,
,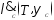 .
.
