
- •Матрицы и операции над ними
- •2. Определение. Элементарными преобразованиями матрицы:
- •3.Обратная матрица
- •4. Определитель и его свойства
- •5. Алг. Дополнение. Свойства определителей
- •6. Миноры. Ранг, его свойства и нахождение
- •7. Слау т. Кронекера-капелли
- •8. Метод Гаусса
- •9. Метод Краммера
- •10 .Матричный метод решения
- •11. Разложение определителя по элементам строки или столбца
- •12. Слау 3 порядка
- •5.Теорема Лапласа
- •13 . Условие существования нетривиальных решений однородной системы и их нахождение
- •14.Базисные и свободные переменные слау. Фундаментальная система решений
Матрицы и операции над ними
![]()




![]()



2. Определение. Элементарными преобразованиями матрицы:
1) умножение строки на число, отличное от нуля;
2) прибавление к элементам одной строки элементов другой строки;
3) перестановка строк;
4) вычеркивание (удаление) одной из одинаковых строк (столбцов);
5) транспонирование
Ступенчатой называется матрица, удовлетворяющая следующим условиям:
если эта матрица содержит нулевую строку (т.е. строку, все элементы которой равны нулю), то все строки, расположенные под нею, также нулевые;
если первый ненулевой
элемент некоторой строки расположен в
столбце с номером ![]() ,
то первый ненулевой элемент следующей
строки должен находиться в столбце с
номером большим, чем
,
то первый ненулевой элемент следующей
строки должен находиться в столбце с
номером большим, чем![]() .
.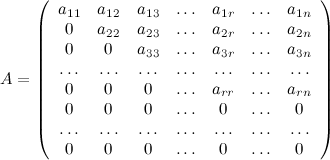
Ступенчатой называется
матрица, которая содержит ![]() строк
и у которой первые
строк
и у которой первые![]() диагональных
элементов ненулевые, а элементы, лежащие
ниже главной диагонали и элементы
последних
диагональных
элементов ненулевые, а элементы, лежащие
ниже главной диагонали и элементы
последних![]() строк
равны нулю, то есть это матрица вида:
строк
равны нулю, то есть это матрица вида:
3.Обратная матрица
Определение:
Матрица
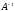 называется обратной по отношению к
квадратной матрице
называется обратной по отношению к
квадратной матрице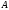 ,
если
,
если
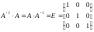 .
.
Обратная матрица
существует только для квадратной
матрицы, определитель которой не равен
нулю. Такая матрица называется
невырожденной.
Так как
 ,
то обратная матрица
,
то обратная матрица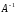 существует.
существует.
Укажем следующие свойства обратных матриц:
(A-1)-1 = A;
(AB)-1 = B-1A-1
(AT)-1 = (A-1)T.
4. Определитель и его свойства
Для каждой квадратной матрицы определено число, называемое определителем матрицы.Определителем матрицы первого порядка называется число, равное единственному
элементу этой матрицы: A = {a}, detA = |A| = a.
Свойства определителей:
1.
При транспонировании квадратной матрицы её
определитель не меняется: ![]()
2. Общий множитель в строке можно выносить за знак определителя.
Пример
![]()
3. ![]()
То
есть, если квадратная матрица ![]()
![]() -го
порядка умножается на некоторое
ненулевое число
-го
порядка умножается на некоторое
ненулевое число![]() ,
то определитель полученной матрицы равен
произведению определителя исходной матрицы
,
то определитель полученной матрицы равен
произведению определителя исходной матрицы![]() на
число
на
число![]() в
степени, равной порядку матриц.
в
степени, равной порядку матриц.
Пример
Задание. Пусть
определитель матрицы ![]() третьего
порядка равен 3, вычислить
определитель матрицы
третьего
порядка равен 3, вычислить
определитель матрицы![]() .
.
Решение. По
свойству ![]()
Ответ. ![]()
4. Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.

5. Если две строки определителя поменять местами, то определитель поменяет знак.
Пример
![]()
6. Определитель с двумя равными строками равен нулю.
Пример
![]()
7. Определитель с двумя пропорциональными строками равен нулю.
Пример
![]()
8. Определитель, содержащий нулевую строку, равен нулю.
Пример
![]()
9. Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.
Пример
Пусть
задан определитель третьего порядка ![]() .
Прибавим ко второй строке определителятретью
его строку, при этом значение определителя не
измениться:
.
Прибавим ко второй строке определителятретью
его строку, при этом значение определителя не
измениться:
![]()
10. Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
Пример
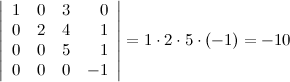
11.
Определитель произведения матриц равен
произведению определителей: ![]()
