
- •Предисловие
- •Глава 1. Введение
- •1.1. Предмет строительной механики и ее задачи
- •1.2. Кинематический анализ сооружений
- •1.2.1. Связи и их реакции
- •1.2.2. Степени свободы и статическая определимость системы
- •1.2.3. Изменяемые системы
- •1.2.4. Способы образования и структурный анализ
- •1.2.5. Аналитическое исследование системы
- •1.3. Основные уравнения строительной механики
- •Глава 2. Расчет статически определимых стержневых систем
- •2.1. Свойства статически определимых систем
- •2.2. Внутренние усилия в рамах
- •2.2.1. Определения и порядок построения эпюр
- •2.2.2. Построение эпюр в простых рамах
- •2.2.3. Построение эпюр в составных рамах
- •2.3. Расчет плоских ферм
- •2.3.1. Основные понятия
- •2.3.2. Метод сечений
- •2.3.3. Метод вырезания узлов
- •2.4. Расчет трехшарнирных арок
- •2.4.1. Основные понятия
- •2.4.2. Внутренние усилия в арке
- •2.4.3. Рациональная ось арки
- •Глава 3. Определение перемещений в
- •3.1. Работа сил, приложенных к твердому телу
- •3.2. Работа сил, приложенных к деформируемому телу
- •3.3. Общие теоремы строительной механики
- •3.4. Работа внутренних сил плоской стержневой системы
- •3.5. Интеграл Мора-Максвелла
- •3.6. Формула Верещагина
- •3.7. Примеры определения перемещений
- •Глава 4. Расчет статически неопределимых балок и рам методом сил
- •4.1. Свойства статически неопределимых систем
- •4.2. Суть метода сил. Канонические уравнения мс
- •4.3. Определение внутренних усилий
- •4.4. Проверка правильности решения
- •4.5. О выборе ос мс. Признаки ортогональности эпюр
- •4.6. Расчет симметричных систем
- •4.7. Расчет неразрезных балок
- •Глава 5. Расчет статически неопределимых арок и ферм методом сил
- •5.1. Расчет статически неопределимых ферм
- •5.2. Расчет статически неопределимых арок
- •Глава 6. Расчет статически неопределимых систем методом перемещений
- •6.1. Суть метода перемещений. Основная система мп
- •6.2. Канонические уравнения метода перемещений
- •6.3. Вычисление коэффициентов канонических уравнений
- •6.4. Общий метод вычисление коэффициентов
- •Глава 7. Понятие о расчете снс методом конечных элементов
- •7.1. Суть метода конечных элементов
- •7.2. Применение мкэ для расчета стержневых систем
- •Литература
- •Оглавление
6.4. Общий метод вычисление коэффициентов
Рассмотренный выше метод вычисления коэффициентов и свободных членов канонических уравнений МП, основанный на рассмотрении равновесия узлов рамы, приводит к затруднениям для рам с наклонными элементами. В этом случае, а также при реализации МП в компьютерной программе целесообразно воспользоваться общим методом вычисления коэффициентов.
Пусть рама загружена произвольной нагрузкой (рис. 6.6, а), а соответствующая ей основная система МП, образована введением двух связей: моментной – i и линейной – j (рис. 6.6, б).
Рассмотрим два состояния этой системы, соответствующие единичным смещениям введенных связей, и обозначим через`Mi0 и`Mj0 соответствующие им эпюры изгибающих моментов (рис. 6.6, в, г).
Вычислим работу внешних сил первого состояния системы на перемещениях второго состояния:
A12 =rii·θij+ rji·δjj=rii· 0 + rji·1 =rji.
Учитывая, что с учетом (3.15):
A12= –W12= –Sò(`Mi0·`Mj0/EJ )ds,
получим отсюда искомое выражение для определения удельных реакций:
rij = rji = Sò(`Mi0·`Mj0/EJ )ds . (6.4)
Последнее выражение напоминает формулу (4.4) для вычисления коэффициентов канонических уравнений в методе сил:
ij = (`Mi0 ´`Mj0) = (Mi0Mj0 /EJ)ds,
и может показаться, что свободные члены системы канонических уравнений в методе перемещений также можно вычислить по формуле, аналогичной (4.5):
Dip0= (`Mi0 ´`Mp0) = (Mi0Mp0 /EJ)ds.
В действительности это не так: Rip0 ≠ (`Mi0 ´`Mp0), а (`Mi0 ´`Mp0) = 0.
Рассмотрим снова два состояния основной системы метода перемещений. Пусть первое по-прежнему соответствует единичному смещению i-ой связи (рис. 6.6, в), а второе – единичной силе, приложенной в k-ой точке этой системы (рис. 6.6, д).
Работа внешних сил первого состояния системы на перемещениях второго состояния равна нулю: A12 = rii · θip+ rji · δjp = rii · 0 + rji · 0 = 0, а поскольку A12 = A21 , то
A21 = P · pi + rip· θii = 0,
откуда
rip = – pi .
То есть реакция в i-ой связи основной системы от единичной силы, приложенной в точке k , равна взятому со знаком минус перемещению точки приложения силы от единичного смещения этой связи.
Это утверждение носит название второй теоремы Релея.
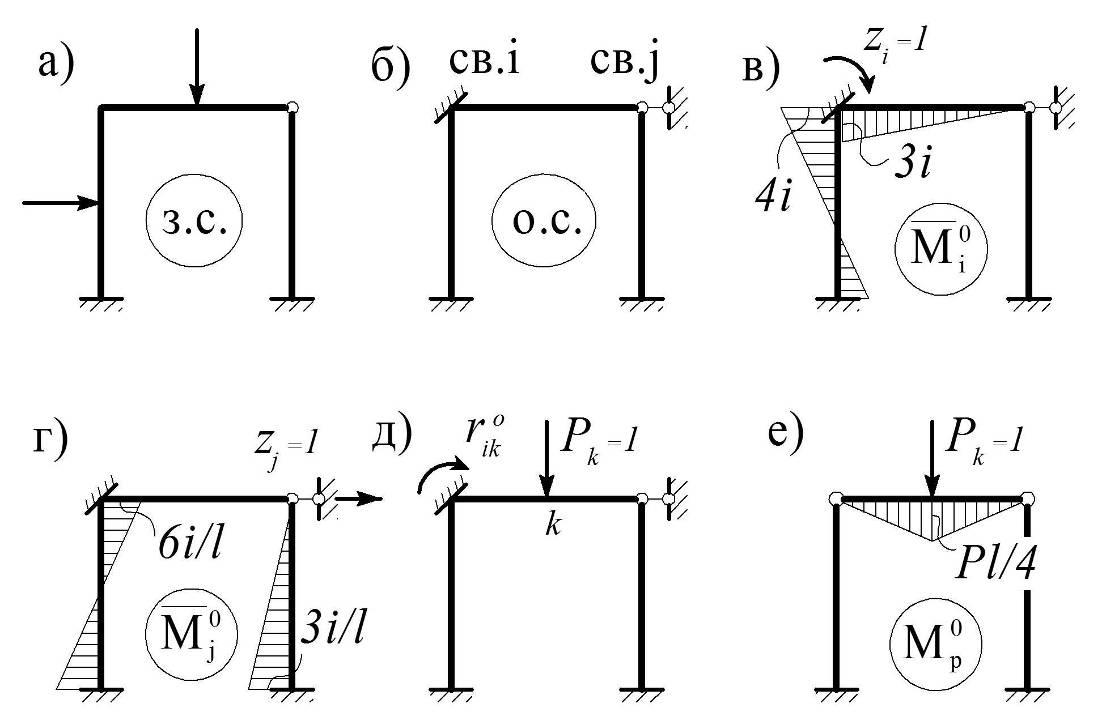
Рис. 6.6
Возвращаясь к традиционным обозначениям МП и обобщая последнее соотношение на случай нескольких сил произвольной величины, получим:
Rip0 = – Pk · ki . (6.5)
Таким образом, реакция в i-ой связи ОС МП от заданной нагрузки равна взятой со знаком минус работе всех сил, приложенных к системе на перемещениях, вызванных единичным смещением этой связи.
Примечание.
Поскольку A12 = 0, а A12 = – W12 , то действительно: (`Mi0 ´`Mp0) = – W12 = 0. При этом нетрудно доказать, что искомую реакцию можно вычислить по формуле:
Rip0 = (`Mi0 ´ Mp0) = – Σ(`Mi0 ´ Mp0/ EJ)ds,
где `Mi0 – по-прежнему эпюра моментов в ОС МП от единичного смещения i-ой связи, а Mp0 – эпюра моментов в любой ОС МС от заданной нагрузки. Такой, например, является эпюра, приведенная на рис. 6.6, е.
Легко убедиться, что в этом случае значение Rip0 = – 3Pl/16 совпадает с табличным значением, указанным на рис. 6.4.
