3.6. Формула Верещагина
Интеграл (3.17) можно вычислить аналитически, однако если жесткости стержней постоянны, удобнее воспользоваться другим способом, который обычно и применяют на практике.
Учитывая, что эпюра`Mi от единичного силового фактора является кусочно-линейной, можно выбрать промежутки a,b, где она будет просто линейной. Тогда выбирая начало локальной системы отсчета так, как показано на рис. 3.12, б, ее уравнение можно записать в виде: `Mi(x) = tgx. При этом интеграл в (3.17) примет вид:
(
MpMi
/EJ)dx
= (tg/EJ)
x
Mp
dx. (3.19)
Рис.3.12
Обозначая через площадь эпюры Mp:
=
d
=
Mp
dx
,
и учитывая, что ее статический момент относительно оси Oy равен:
Sy
=
xd
= xc,
представим (3.19) в виде:
(tg/EJ)
x
Mp
dx
= (tg/EJ)
xd=
(tg/EJ)
xc
= (yc)/EJ,
где yc = tgxc.
Возвращаясь к формуле (3.17), получим:
ip = (kyck)/(EJk). (3.20)
Таким образом, чтобы перемножить две эпюры, из которых хотя бы одна является линейной, нужно вычислить площадь криволинейной эпюры – и умножить ее на ординату yc в линейной эпюре, вычисленную под центром тяжести криволинейной.
Для реализации формулы (3.20) остается рассмотреть геометрические характеристики стандартных эпюр (рис. 3.13), где две последние – соответствуют эпюрам от равномерно распределенной нагрузки. Поскольку любую нестандартную эпюру можно представить комбинацией стандартных, с помощью последних можно перемножить произвольные эпюры.
Рис.3.13
Примечания:
1. При выводе формулы (3.20) криволинейная эпюра Mp с площадью w предполагается однозначной. Если это условие не выполнено, ее представляют комбинацией двух или большего числа стандартных эпюр.
2. Для вычисления интеграла (3.17) можно применять формулы численного интегрирования, в том числе – формулу Симпсона:
=
(b
–
a)/6
f(a)
+ 4f
(a
+ b)/2
+ f(b),
которая позволяет получить точный результат, если функция f (x) является многочленом до третьей степени включительно.
Таким образом, если на всем промежутке a,b эпюра `Mi линейна, а эпюра Mp является квадратичной параболой, интеграл (3.17) можно вычислить по формуле:
Dip=(lk/6EJk) Mp(ak) `Mi(ak) +4 Mp (ak +bk)/2 `Mi (ak+bk)/2+Mp(bk) `Mi(bk) . (3.21)
При этом однозначности эпюры Mp на промежутке a,b не требуется, а формулу можно, конечно, применять и для линейной функции Mp(x).
3.7. Примеры определения перемещений
Рассмотрим примеры определения перемещений в СОС от действующей нагрузки. Во всех случаях изгибная жесткость элементов системы – EJ и их продольная жесткость – EF предполагаются известными.
Пример 3.1. Определить максимальные прогибы балки (рис. 3.14, а).
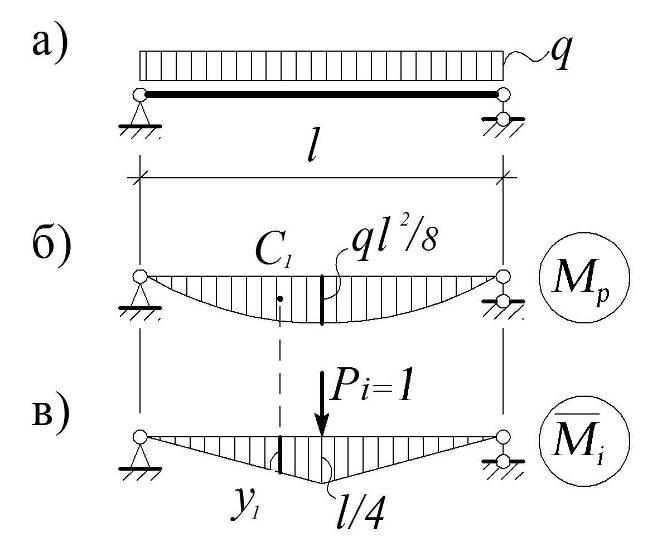
Рис.3.14
Решение. В соответствии с формулой (3.17) строим эпюру Mp от заданной нагрузки (рис. 3.14, б) и эпюру Mi от единичной силы, приложенной в середине балки (рис. 3.14, в).
Вычислим интеграл (3.17) по формуле Верещагина. На всем промежутке 0,l эпюра Mp является однозначной, то есть отвечает предъявляемым к ней требованиям, а эпюраMi на всем промежутке 0,l будет нелинейной. Поэтому область интегрирования делим на два участка: 0, l/2 и l/2, l, на каждом из которых Mi(x) будет линейной. С учетом симметрии получим:
vmax = ip = 2 (w1 yc1)/EJ = 2 (2/3)( l/2)(ql2/8)(5/8)(l/4) = 5ql4/384EJ.
Для того чтобы получить тот же результат с помощью интегрирования дифференциального уравнения изогнутой оси балки, нужно затратить примерно втрое больше усилий – хотя бы потому, что придется находить угол поворота балки в ее начальном сечении – 0.
Формально воспользовавшись для всего промежутка 0,l формулой Симпсона (3.21), и учитывая, что значения Mp иMi на его концах равны нулю, получим:
vmax = (l/6EJ)4(ql2/8)(l/4) = ql4/48EJ.
Найденный результат оказался неверным, поскольку на всем промежутке 0,l подынтегральная функция f(x) = Mp(x) Mi (x) не отвечает требованиям, предъявляемым к ней этой формулой.
Пример 3.2. Найти линейное и угловое перемещения точки A на конце Г-образной консольной рамы, у которой жесткость стойки вдвое больше жесткости ригеля (рис. 3.15, а).
Рис.3.15
Решение. Строим эпюру Mp от заданной нагрузки и эпюрыMi от единичных сил и моментов, приложенных в точке A (рис. 3.15, б-д).
Определяем вертикальное перемещение точки А, перемножая эпюры Mp иM в:
в = (Mp M в) = (1/EJ) w1 y1 + (1/2EJ) w2 y2 = (1/EJ)(1/3)l (ql2/2)(3/4)l +
+ (1/2EJ) l(ql2/2)l = (3/8)(ql4/EJ).
Находим горизонтальное перемещение точки А:
г = (Mp M г) = (1/2EJ) l(ql2/2)(l/2) = (1/8)(ql4/EJ).
Полное перемещение точки А составит:
___________ __
А = (в)2 + (г)2 = (10 ql4)/8EJ.
Угол поворота сечения в точке А будет равен:
А = (Mp M у) = (1/EJ) w1×1 + + (1/2EJ) w2×1 = (1/EJ)(1/3)l (ql2/2)1 +
+ (1/2EJ) l(ql2/2)1 = (5ql3/12EJ ).
Рассмотренный пример наглядно показывает, почему при определении перемещений в рамах мы пренебрегаем продольными деформациями. Вертикальное перемещение точки А от заданной нагрузки в основном определяется изгибом ригеля, изгибом стойки и только в очень незначительной степени – ее сжатием.
Пример 3.3. Найти угол поворота сечения на правой опоре рамы, рассмотренной в примере 2.5, полагая EJ = const (рис. 2.9, а).
Рис.3.16
Решение. Воспользуемся уже построенной ранее эпюрой Mp от заданной нагрузки (рис. 2.9, б) и (рис. 3.16, а), и умножим ее на эпюру`Mi от единичного момента (рис. 3.16, б). На левой стойке и ригеле эпюра Mp представлена тремя треугольниками с равной площадью wтр = (1/2)l (ql2/4), которые умножаются на три одинаковых треугольника в эпюре `Mi.
Нестандартную эпюру Mp на правой стойке с площадью wпар представим суммой стандартных эпюр: параболы с площадью w1 и треугольника с площадью w2 (рис. 3.16, в).
Поскольку перемножаемые эпюры расположены на разных волокнах, результат получится со знаком минус. Как и при определении опорных реакций, это означает, что действительное направление угла поворота будет противоположно направлению, указанному на рисунке:
В = (Mp Mi) = (1/EJ) (–3) wтр yтр - wпар yпар = – (1/EJ) 3wтр yтр+w1 y1+
+w2 y2 = – (1/EJ) 3 (1/2) l (ql2/4) (2/3)(1/2) + (2/3) l (ql2/8) [(1/2)(1/2+1) + (1/2) l (ql2/4) [(2/3)(1/2) + (1/3)×1] = – (11ql3) / (48EJ).