
- •Глава 2 векторная алгебра
- •§1. Векторы и действия над ними
- •§2. Скалярное произведение
- •§3. Векторное произведение
- •§4. Смешанное произведение
- •Глава 3 прямая и плоскость
- •§1. Прямая на плоскости
- •§2. Уравнение плоскости
- •§3. Прямая в пространстве
- •§4. Прямая и плоскость
- •1.3.1. Векторное произведение
- •1.4.1. Смешанное произведение
- •2.1.1. Прямая на плоскости
- •Список литературы
§3. Прямая в пространстве
Составить каноническое уравнение прямой, проходящей через точку M1(2, 0, – 3) параллельно:
1)
вектору
![]() = {2; – 3; 5};2)
прямой
= {2; – 3; 5};2)
прямой
![]() ;
;
3) оси 0x; 4) оси 0y; 5) оси 0z.
Составить каноническое уравнение прямой, проходящей через две данные точки:
1) (1, – 2, 1), (3, 1, – 1); 2) (3, – 1, 0), (1, 0, – 3);
3) (0, – 2, 3), (3, – 2, 1); 4) (1, 2, – 4), (– 1, 2, – 4).
Составить параметрическое уравнение прямой, проходящей через точку M1(1, – 1, – 3) параллельно:
1)
вектору
![]() = {2; – 3; 4};2)
прямой
= {2; – 3; 4};2)
прямой
![]() ;
;
3) прямой x = 3t – 1, y = –2t + 3, z = 5t + 2.
Составить параметрическое уравнение прямой, проходящей через две данные точки:
1) (3, – 1, 2), (2, 1, 1); 2) (1, 1, – 2), (3, – 1, 0); 3) (0, 0, 1), (0, 1, – 2).
Через точки M1(– 6, 6, 5) и M2(12, – 6, 1) проведена прямая. Определить точки пересечения этой прямой с координатными плоскостями.
Даны вершины треугольника A(3, 6, – 7), B(– 5, 2, 3) и C(4, –7, – 2). Составить параметрические уравнения его медианы, проведенной из вершины C.
Даны вершины треугольника A(3, – 1, – 1), B(1, 2, – 7) и C( – 5, 14, –3). Составить канонические уравнения биссектрисы его внутреннего угла при вершине C.
Составить каноническое уравнение прямой, проходящей через точку M1(2, 3, – 5) параллельно прямой

Составить канонические уравнения следующих прямых:
Составить параметрические уравнения следующих прямых:
1)

2)

Доказать параллельность прямых:
1)
![]() и
и

2)
x
= 2t
+ 5, y
= –t
+ 2, z
= t
– 7 и

3)
 и
и

Доказать перпендикулярность прямых:
1)
![]() и
и

2)
 и
и
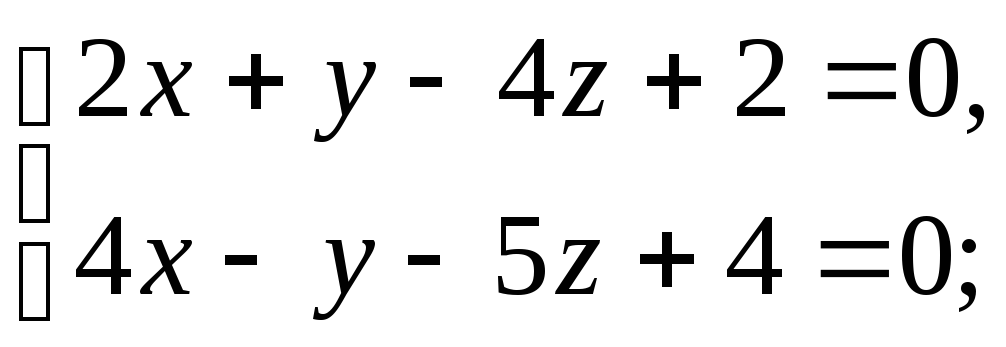
3)
 и
и

Найти острый угол между прямыми:
 и
и .
.Найти тупой угол между прямыми x = 3t – 2, y = 0, z = – t + 3 и
x = 2t – 1, y = 0, z = t – 3.
Определить косинус угла между прямыми:
 и
и

Доказать, что прямые, заданные параметрическими уравнениями x = 2t – 3, y = 3t – 2, z = – 4t + 6 и x = t + 5, y = – 4t – 1, z = t – 4, пересекаются.
Даны прямые
 и
и .
При каком значенииl
они пересекаются ?
.
При каком значенииl
они пересекаются ? Составить уравнения прямой, которая проходит через точку M1(– 1, 2, – 3) перпендикулярно к вектору
 = {6; – 2; – 3} и пересекает прямую
= {6; – 2; – 3} и пересекает прямую .
.Составить уравнения прямой, которая проходит через точку M1(– , –5, 3) и пересекает две прямые:
 и
и .
.Составить параметрические уравнения общего перпендикуляра двух прямых, заданных уравнениями x = 3t – 7, y = –2t + 4, z = 3t + 4 и x = t + 1, y = 2t – 8, z = – t – 12.
Найти следы прямых x = z + 5, y = 4 – 2z и
 на плоскостяхx0y
и x0z
и построить прямые.
на плоскостяхx0y
и x0z
и построить прямые.
Указание: Положить в уравнениях прямой 1) z = 0; 2) y = 0.
Уравнения прямой x + 2y + 3z – 13 = 0, 3x + y + 4z – 14 = 0 написать: 1) в проекциях; 2) в канонической форме. Найти следы прямой на координатных плоскостях, построить прямую и ее проекции.
Написать уравнение прямой, проходящей через точку A(4, 3, 0) и параллельно вектору
 {
– 1; 1; 1} . Найти след прямой на плоскостиy0z
и построить прямую.
{
– 1; 1; 1} . Найти след прямой на плоскостиy0z
и построить прямую. Построить прямую x = 4, y = 3 и найти ее направляющий вектор.
Построить прямые: 1) y = 3, z = 3; 2) y = 2, z = x + 1; 3) x = 4, z = y. Определить их направляющие векторы.
Написать уравнения прямой, проходящей через точки A(– 1, 2, 3) и B(2, 6, – 2), и найти ее направляющие косинусы.
Построить прямую, проходящую через точки A(2, – 1, 3) и B(2, 3, 3), и написать ее уравнения.
Написать уравнения траектории точки M(x, y, z), которая, выйдя из точки A(4, – 3, 1), движется со скоростью v{ 2; 3; 1}.
Написать параметрические уравнения прямой:
1)
проходящей через точку (– 2, 1, – 1),
параллельно вектору
![]() {1;
–2; 3};
{1;
–2; 3};
2) проходящей через точки A(3, – 1, 4) и B(1, 1, 2).
Написать уравнения прямой, проходящей через точки (a, b, c):
1) параллельно оси 0z;
2) перпендикулярно к оси 0z.
Найти угол прямой x = 2z – 1, y = – 2z + 1 с прямой, проходящей через начало координат и через точку (1, – 1, – 1).
Найти угол между прямыми: x – y + z – 4 = 0, 2x + y – 2z + 5 = 0 и x + y + z – 4 = 0, 2x + 3y – z – 6 = 0 .
Указание:
Направляющий
вектор каждой из прямых можно определить
как векторное произведение нормальных
векторов плоскостей
![]() =
=![]() .
.
Показать, что прямая
 перпендикулярна к прямойx
= z
+ 1, y
= 1 – z.
перпендикулярна к прямойx
= z
+ 1, y
= 1 – z.Написать уравнения прямой, проходящей через точку (– 4, 3, 0), параллельно прямой x – 2y + z = 4, 2x + y – z = 0.
Написать уравнение перпендикуляра, опущенного из точки (2, – 3, 4) на ось 0z.
Указание: Искомая прямая проходит еще через точку (0, 0, 4).
Найти расстояние от точки M(2, – 1, 3) до прямой
 .
.
Указание: Точка
A(–
1, – 2, 1) лежит на прямой;
![]() {3;
4; 5} – направляющий вектор прямой.
Тогда
{3;
4; 5} – направляющий вектор прямой.
Тогда
d
= AM
sin
=
![]() .
.
Найти расстояние между параллельными прямыми
![]() и
и
![]() .
.



