Глава 2 векторная алгебра
§1. Векторы и действия над ними
1. Вычислить
модуль вектора
.
2. Даны
координаты вектора x
= 4, y
= –12. Определить третью координату z
при условии, что |
|
= 13.
3. Даны
точк A(3,
–1, 2) и B(–1,
2, 1). Найти координаты векторов
и
.
4. Дан
модуль вектора |
|
= 2 и углы
= 45,
=
60,
= 120,
которые составляет вектор с осями
координат. Вычислить проекции вектора
на координатные оси.
5.
Вычислить направляющие косинусы вектора
{12;
–15; –16}.
6. Определить координаты точки M, если ее радиус-вектор составляет с координатными осями одинаковые углы и его модуль равен 3.
7. Как
должны быть связаны ненулевые векторы
и
,
чтобы имело место соотношение: 1)
;
2)
.
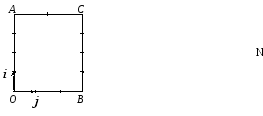
8. По
сторонам OA
и OB
прямоугольника OACB
отложены единичные векторы
и
(см.
рис.1.3). Выразить через
и
векторы
если |
|
= 4 и |
|
= 3.
Рис. 1.3
9. Построить
вектор
=2
+3
+6
,
определить его длину и направление
(проверить по формуле
).
10. Радиус-вектор
точки M
составляет с осью Ox
угол 45
и с осью Oy
угол 60.
Длина его r
= |
|=
6 . Определить координаты точки M,
если ее координата z
отрицательна, и выразить вектор
через орты
,
,
.
11. Даны
точки A(1,
2, 3) и B(3,
–4, 6). Построить вектор
=
,
его проекции на оси координат и определить
длину и направление вектора. Построить
углы вектора
с осями координат.
12. Построить
параллелограмм на векторах
и определить его диагонали.
13. Даны три последовательные вершины параллелограмма A(1, –2, 3), B(3, 2, 1) и C(6, 4, 4). Найти его четвертую вершину D.
Указание.
Из равенства
следует, что равны и их координаты:x
– 1 = 6 – 3 и
т.д.
14. На
плоскости xOy
построить векторы:
.
Разложить геометрически и аналитически
вектор
по векторам
и
.
15. Установить,
в каких случаях тройки векторов
,
и
будут линейно зависимы, и в том случае,
когда это возможно, представить вектор
как линейную комбинацию векторов
и
:
1)
={5;
2; 1};
={–1;
4; 2};
={–1;
–1; 6};
2)
={6;
4; 2};
={–9;
6; 3};
={–3;
6; 3};
3)
={6;
–18; 12};
={–8;
24; –16};
={8;
7; 3}.
16.
Даны: |
|
= 13; |
|
= 19 и |
+
|
= 24. Вычислить |
–
|.
17. Проверить
коллинеарность векторов
=
{2; –1; 3} и
=
{–6; 3; –9}. Установить, какой из них длиннее
и во сколько раз, как они направлены - в
одну или в противоположные стороны.
18. Определить,
при каких значениях
и
векторы
= –2
+3
+
и
=
–6
+2
коллинеарны.
19. Проверить, что четыре точки A (3, –1, 2), B (1, 2, –1), C (–1, 1, –3), D (3, –5, 3) служат вершинами трапеции.
§2. Скалярное произведение
Векторы
и
образуют угол 2/3.
Зная, что |
|
= 3;и|
|
= 4, вычислить:
20.
;21.
(
+
)2
;
22.
(3
–2
)(
+2
);
23.
2;
24.
(
–
)2;
25.
(3
+2
)2.
26. Определить
угол между векторами
= –
+
и
=
–2
+2
.
27. Определить углы ABC с вершинами A(2; –1; 3), B(1; 1; 1) и C(0; 0; 5).
28.
Даны векторы
=
{4; –2; –4} и
=
{6; –3; 2}. Вычислить скалярное произведение
векторов 2
–3
и
+2
.
29. Найти
угол между диагоналями параллелограмма,
построенного на векторах
= 2
+
и
=
–2
+
.
30. Даны
векторы
=
+
+2
и
=
–
+4
.
Определить
и
.
31. Раскрыть
скобки в выражении (2
–
)·
+(
–2
)·
+(
–2
)2.
32.
Дан вектор
=2
–
, где
и
– единичные векторы с углом 120
между ними. Найти
и
.
33. Какому
условию должны удовлетворять векторы
и
,
чтобы вектор
+
был перпендикулярен вектору
–
.
34. Даны
единичные векторы
,
и
,
удовлетворяющие условию
+
+
=
0. Вычислить
·
+
·
+
·
.
35. Дано:
|
|
= 3; |
|
= 5. Определить, при каком значении
векторы (
+·
),
(
–·
)
будут взаимно перпендикулярны.
36. Даны
три вектора:
,
и
.
Вычислить
.
37.
38.
39.