
chirskii-lectures-4sem
.pdf
Практически всегда D представляет собой криволинейную трапецию или конечное объединение криволинейных трапеций. Можно считать, что и разбиение D на части Di определяется с помощью непрерывных кривых, то
есть все Di также криволинейные трапеции или их объединения. |
|
|||
В одномерном случае |
мы рассматривали |
длины |
частей |
разбиения |
∆xi = xi+1 − xi . В двумерном |
случае обобщением |
понятия |
длины |
∆xi будет |
площадь Di. Однако нам потребуется также понятие диаметра множества D , обозначаемого diam(D). Эта величина определяется как точная верхняя грань расстояний между точками множества D. В частности, если D – круг, то diam(D) – это как раз длина диаметра круга в привычном смысле. В общем случае это понятие поясняет рисунок:
1

Ясно, что если diam(Di) невелик, то и площадь Di также невелика, поскольку неравенство diam(Di ) <δ означает, что Di
содержится в некотором круге радиуса δ, и, значит имеет площадь не больше, чем πδ 2 .
Действительно, возьмём произвольную точку множества D в качестве центра этого круга. Так как diam(Di ) < δ , остальные точки Di лежат внутри круга.
Однако площадь круга может быть невелика, а diam(Di) достаточно велик. Пример – очень тонкий прямоугольник.
Определим диаметр d(T) разбиения T как наибольший из диаметров
diam(Di) частей этого разбиения. |
|
|
|
|
|
|
|||
Далее, как |
и |
в |
одномерном |
случае, |
выберем |
точки |
Ni Di |
(было: |
|
ξi [xi−1; xi ]). Пусть Ni |
имеет координаты (ξi ,ηi ). Важную роль в дальнейшем |
||||||||
будет играть понятие интегральной суммы |
∑n |
f (ξi ,ηi |
) пл(Di |
)=σ(f ,T ,{Ni }). |
|||||
|
|
|
|
|
i=1 |
|
|
|
|
Так же, как |
и |
в |
одномерном |
случае, |
эта величина |
имеет |
простой |
||
2
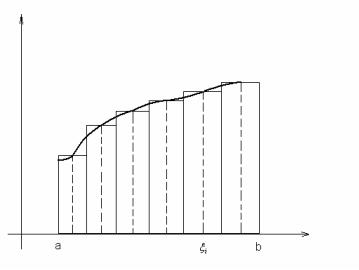
n
геометрический смысл. Вспомним, что сумма ∑ f (ξi )∆xi представляла собой
i=1
площадь ступенчатой фигуры вида:
|
(для простоты считаем, что |
f (x) ≥ 0 ). |
|
|
|
|
|||
|
Вспомним также, что объём цилиндра с основанием, имеющим площадь |
||||||||
S и с высотой h равен S h . |
|
|
|
|
|
|
|||
|
|
|
|
|
n |
|
|
|
|
|
Поэтому |
|
интегральная сумма |
∑ f (ξi ,ηi )пл(Di ) |
равна |
объёму |
тела, |
||
|
|
|
|
|
i=1 |
|
|
|
|
состоящего из цилиндров с высотой |
f (ξi ,ηi ) |
(для |
простоты |
считаем, что |
|||||
|
f (x, y) ≥ 0 ) и основаниями Di . |
|
|
|
|
|
|
||
|
Определение. Пусть f (x, y) |
- ограниченная на квадрируемом множестве |
|||||||
D функция. |
|
Пусть I R . |
Если |
ε > 0 |
δ > 0 |
T : d(T ) <δ |
{Ni } |
||
|
σ( f ,T ,{Ni }) − I |
|
<ε , то будем говорить, |
что f – интегрируема на D функция и |
|||||
|
|
||||||||
I = ∫∫ f (x, y)dxdy .
D
Замечание. Это определение несколько отличается от одномерного, в котором отсутствовало требование ограниченности функции f (x) . Мы тогда доказывали необходимое условие интегрируемости: если f (x) интегрируема на [a,b], то f (x) ограничена на [a,b]. Здесь условие ограниченности включено в определение.
3

Критерий существования ∫b f (x)dx формулировался в терминах сумм
|
|
|
|
a |
|
|
|
|
|
n |
|
|
n |
|
f (x), |
|
f (x), то |
Дарбу вида s(T ) = ∑mi ∆xi , |
S(T ) = |
∑Mi ∆xi , где mi = inf |
Mi = sup |
|||||
|
i=1 |
|
|
i=1 |
x [ xi−1 ;xi ] |
x [ xi−1 ;xi ] |
|
|
|
|
|
|
|
|
|||
есть mi - нижняя грань, а Mi |
- |
верхняя грань множества значений |
f (x) при |
|||||
x [xi−1; xi ]. |
|
|
|
|
|
|
|
|
Аналогично |
обозначим |
для ограниченной |
на D |
функции f (N) |
||||
mi = inf f (N ) , Mi |
= sup f (N ) |
(эти |
числа существуют |
ввиду |
предполагаемой |
|||
N Di |
N Di |
|
|
|
|
|
|
|
ограниченности
Нижняя сумма Дарбу Верхняя сумма Дарбу
f(N) на D и, значит, на всех Di и определим суммы Дарбу равенствами
s(T )= ∑n |
mi пл(Di ), |
S(T )= ∑n |
M i пл(Di ). Эти величины представляют собой |
i=1 |
|
i=1 |
|
объемы тел, состоящих из цилиндров с основаниями Di и высотами, соответственно тi и Мi. Ясно, что при любом выборе {Ni} s(T )≤σ(f ,T ,{Ni })≤ S(T ).
Вполне аналогично одномерному случаю можно доказать критерий интегрируемости.
Теорема. Ограниченная f(x,y) интегрируема на квадрируемом множестве D ε > 0 δ > 0 T : d(T )<δ S(T )− s(t)<ε
4
(На экзамене ограничиваемся формулировкой). Из этого критерия следует теорема.
Теорема. Если f(x,y) непрерывна на квадрируемом множестве D, то f(x,y) интегрируема на этом множестве.
(На экзамене достаточно формулировки).
|
|
2. |
Свойства двойных интегралов |
|
|
|
|
|||||||||||
Свойство 1. Если f1, f 2 - интегрируемые на D функции, а α1, α2 - числа, |
||||||||||||||||||
то ∫∫(α1 f1 |
+α2 f2 )dxdy =α1 ∫∫ f1dxdy +α2 ∫∫ f2 dxdy . Иными словами, интеграл - |
|||||||||||||||||
D |
|
|
|
|
D |
|
|
|
|
D |
|
|
|
|
|
|
|
|
линейный функционал. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Свойство 2. Если f |
- интегрируема на D1 D2 , причем если площадь |
|||||||||||||||||
пересечения |
D1 D2 |
равна |
0, |
|
то |
∫∫ |
fdxdy = ∫∫ fdxdy + ∫∫ fdxdy . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
D1 D2 |
D1 |
|
|
D2 |
|
(Аддитивность интеграла по множеству). |
|
|
|
|
|
|
|
|||||||||||
Свойство |
3. |
Если |
f - интегрируемая |
на |
D функция |
и |
f ≥ 0 , |
то |
||||||||||
∫∫ fdxdy ≥ 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Свойство 4. Если f1, f 2 - интегрируемые на D функции и |
f1 ≥ f2 , то |
|||||||||||||||||
∫∫ f1dxdya ≥ ∫∫ f2 dxdy . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
D |
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Свойство 5. Если f - интегрируемая на D функция, то | f | - также |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
интегрируемая, причем |
∫∫ fdxdy |
≤ ∫∫ |
|
f |
|
dxdy . |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
D |
|
|
D |
|
|
|
|
|
|
|
|
|
||
Свойство 6. Если f - интегрируемая на D функция, причем т < f < М, |
||||||||||||||||||
где т, |
М |
ограничивающие |
множество |
значений |
f |
числа, |
то |
|||||||||||
m пл(D)≤ ∫∫ fdxdy ≤ M пл(D) (пл.(D) |
|
– |
площадь |
D), т.е. |
γ, m ≤ γ ≤ M : |
|||||||||||||
∫∫ fdxdy = γ m(D). Если, |
кроме того, |
|
f - |
непрерывна на D, |
то |
(ξ,η) D : |
||||||||||||
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫ fdxdy = |
f (ξ,η) m(D) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5

Доказывать эти свойства мы не будем - они вполне аналогичны свойствам обычного интеграла.
Можно доказать, что если f - непрерывная на множестве D функция, то
f -интегрируема на D
Свойство 2 позволяет утверждать, что если f имеет разрывы на D лишь вдоль конечного числа непрерывных линий, разбивающих D на квадрируемые области, то f - интегрируема на D, т.к., по свойству 2, интеграл по D, есть просто сумма конечного числа интегралов по полученным частям D (где f - непрерывна и, значит, интегрируема).
3. Вычисление двойных интегралов
Двойной интеграл – новый пока для нас объект, и сначала мы укажем способ его вычисления сведением к более привычным объектам. Сначала рассмотрим двойной интеграл по прямоугольной области D, стороны
которой параллельны осям координат. |
|
|
||
Теорема. Пусть для |
f (x, y) |
существует |
∫∫ f (x, y)dxdy , где |
|
|
|
|
|
D |
D :{(x, y) | a ≤ x ≤ b;c ≤ y ≤ d} . Кроме того, |
пусть для любого x [a,b] существует |
|||
J (x) = ∫d |
f (x.y)dy . |
|
|
|
c |
|
|
|
|
Тогда существует и интеграл, называемый повторным, и имеет место равенство:
6
|
|
|
|
|
|
|
|
∫b J (x)dx = ∫b dx∫d |
f (x, y)dy |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
a |
a c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫ f (x, y)dxdy = ∫b dx∫d |
f (x, y)dy |
|
|
|
|
|
||||
|
|
|
|
|
|
|
D |
|
a |
c |
|
|
|
|
|
|
|
|
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Разобьём прямоугольник D на прямоугольники, обозначенные Dij, |
||||||||||||||||
прямыми, |
параллельными оси y через точки a =xo < x1 |
< ... < xm = b и прямыми, |
|||||||||||||||
параллельными оси x и проходящими через точки c = yo < y1 < ... < yl |
= d. Таким |
||||||||||||||||
образом, Di, j |
={(x, y), x [xi−1 , xi ], y [ y j−1, y j ]}, i =1,...,m, j =1,...k . |
|
|
||||||||||||||
|
Пусть |
∆xi = xi |
− xi−1 , ∆yi |
= yi − yi−1 , |
mi, j и |
M i, j , |
соответственно, |
нижняя |
и |
||||||||
верхняя грани функции |
f (x, y) на Dij, откуда mi, j ≤ f (x, y) ≤ M i, j интегрируем это |
||||||||||||||||
|
|
|
|
|
|
|
y j |
|
|
|
|
|
|
|
|
|
|
неравенство по y: mi, j ∆yi |
≤ ∫ f (ξ, y)dy ≤ M i, j ∆yi . Суммируя эти неравенство по j |
||||||||||||||||
|
|
|
|
|
|
y j −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
k |
|
|
|
|
|
|
|
|
от |
j=1 |
до |
j=k: |
∑mi, j |
∆yi ≤ J (ξi ) ≤ ∑M i, j |
∆yi . Умножим |
все |
части этих |
|||||||||
|
|
|
|
|
j=1 |
|
|
|
j=1 |
|
|
|
|
|
|
|
|
неравенств |
на |
∆xi > 0 |
|
и |
суммируем |
всё |
по |
i |
от |
i=1 |
до |
m: |
|||||
m |
k |
|
|
m |
|
|
m |
k |
|
|
|
|
|
|
|
|
|
∑∑mi, j ∆xi ∆y j ≤∑J (ξi )∆xi |
≤ ∑∑M i, j ∆xi ∆y j . |
|
|
|
|
|
|
|
|||||||||
i=1 j=1 |
|
|
i=1 |
|
|
i=1 j=1 |
|
|
|
|
|
|
|
|
|
||
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
k |
|
|
m |
|
|
m |
k |
|
|
|
|
|
|
|
|
|
∑∑mi, j |
пл.Di, j ≤∑J (ξi )∆xi ≤ ∑∑M i, j |
пл.Di, j |
|
|
|
|
|
|||||||||
|
i=1 j=1 |
|
|
i=1 |
|
|
i=1 j=1 |
|
|
|
|
|
|
|
|
||
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s(T ) ≤ ∑J (ξi )∆xi ≤ S(T ) |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где T – разбиение D на прямоугольники Dij. При d(T ) →0 стремится к |
||||||||||||||||
нулю |
и |
max ∆xi . |
Кроме |
того, |
s(T ), S(T ) →∫∫ fdxdy . |
Значит, |
интеграл |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
b |
d |
|
|
существует и равен ∫∫ f (x, y)dxdy , что и утверждалось. |
|
|
|||||||||||
∫dx∫ f (x, y)dy |
|
|
|||||||||||||||
a |
c |
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
В случае криволинейной трапеции.
7

Справедлива такая теорема:
Теорема (Фубини). Пусть область D задана неравенствами a ≤ x ≤ b ,
Ф1 (x) ≤ y ≤ Ф2 (x) , где Ф1 (x),Ф2 (x) C[a,b] . Пусть существует ∫∫ f (x, y)dxdy и для
D
Ф2 (x )
любого x [a,b] существует J (x) = ∫ f (x, y)dy . Тогда существует интеграл
Ф1 (x )
b |
b |
Ф2 ( x) |
|
∫J (x)dx = ∫dx |
∫ f (x, y)dy и он равен ∫∫ f (x, y)dxdy . |
||
a |
a |
Ф1 ( x) |
D |
Доказательство. Так как Ф1(х) непрерывна на [a,b], существует её минимальное значение c на этом отрезке. Аналогично, существует максимальное значение d функции Ф2(х) на [a, b]. Заключим область D в прямоугольник D*, состоящий из точек (x,y), a ≤ x ≤ b , c ≤ y ≤ d . На этом
f (x, y),если(x, y) D
прямоугольнике рассмотрим функцию f * (x, y) =
0, если(x, y) D* \ D
Условия предыдущей теоремы для f* выполнены. Она интегрируема в D, равна 0 (и, значит, интегрируема) в D*\D. Следовательно, она интегрируема на всей D*. При этом
∫∫ f *dxdy = ∫∫ f *dxdy + ∫∫ |
f *dxdy = ∫∫ fdxdy . |
||
D* |
D |
D*\ D |
D |
Наконец, для любого x [a,b]
d |
Ф1 ( x) |
Ф2 ( x) |
∫ f * (x, y)dy = |
∫ f * (x, y)dy + ∫ |
|
c |
c |
Ф1 ( x) |
d |
Ф2 ( x) |
f * (x, y)dy + ∫ f * (x, y)dy = |
∫ f * (x, y)dy . |
Ф2 ( x) |
Ф1 ( x) |
По доказанному в предыдущей теореме,
b d
∫∫ f *dxdy = ∫dx∫ f * (x, y)dy .
D* |
a |
c |
Откуда сразу получаем:
|
b |
Ф1 ( x) |
∫∫ fdxdy = ∫dx |
∫ f (x, y)dy , |
|
D |
a |
Ф1 ( x) |
Что и требовалось доказать.
8
Следствие: Пусть f(x,y) непрерывна в области D, ограниченной сверху
графиком непрерывной функции y =φ2 (x), снизу - |
y =φ1 (x), |
x [a;b], |
а по |
||
бокам - отрезками вертикальных прямых х = а и х = b. Тогда |
|
|
|||
|
b |
φ2 (x ) |
|
|
|
∫∫ f (x, y)dxdy = ∫dx |
∫ f (x, y)dy . |
|
|
|
|
D |
a |
φ1 (x ) |
|
|
|
Доказательство. Из непрерывности f(x,y) сразу следует её |
|||||
интегрируемость |
на D. |
Кроме того, для любого |
x [a,b] |
функция |
f(x,y) |
непрерывна (а, значит интегрируема по у). Все условия теоремы выполнены.
Замечание. |
|
Если |
|
область |
D |
можно |
|
ограничить |
так: |
|||||
c ≤ y ≤d, ψ1 (y)≤ x ≤ψ1 (y), ψ1 ,ψ2 C[c, d ] , то |
|
|
|
|
|
|||||||||
|
|
|
|
∫∫ f (x, y)dxdy = ∫cd dy∫ψψ12((yy)) f (x, y)dx . |
|
|
|
|||||||
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
Смысл этой теоремы ясен – указан способ сведения нового для нас |
||||||||||||||
объекта – двойного интеграла – к уже изученным обычным интегралам. |
|
|
|
|||||||||||
При вычислении интегралов часто бывает удобно сделать замену |
||||||||||||||
переменных |
|
|
|
|
|
|
x = x(u, v), y = y(u, v) , |
|||||||
где x(u,v), y(u,v), |
∂x |
(u,v), |
∂x |
(u,v), ∂y (u,v), ∂y |
(u,v) |
– |
непрерывны |
|
в |
|||||
∂u |
∂v |
|||||||||||||
|
|
|
|
∂u |
∂v |
|
|
|
|
|
|
|||
некоторой области ∆ R 2 . Впоследствии мы будем часто писать просто |
|
∂x |
|
|||||||||||
|
∂u |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
вместо |
∂x |
(u, v) |
и |
т.п. |
и, кроме |
того, |
говорить |
при выполнении |
||||||
|
||||||||||||||
|
∂u |
|
|
|
|
|
|
|
|
|
|
|
||
вышеупомянутых условий, что x и y – непрерывно дифференцируемые в ∆ функции.
Пусть при этом формулы x = x(u, v), y = y(u, v) задают взаимно-
однозначное отображение квадрируемых областей: D ↔ ∆, (x, y) D, (u, v) ∆ .
Кроме того, не стремясь к минимальности условий, потребуем, чтобы всюду
9

на области ∆ |
|
|||||
|
|
∂x |
∂x |
|
|
|
|
|
|
|
|||
J = |
|
∂u |
∂v |
|
|
не равнялся 0. |
|
|
∂y |
∂y |
|
|
|
|
|
∂u |
∂v |
|
|
|
Теорема. При сформулированных выше условиях для непрерывной на
Dфункции f (x, y) выполняется равенство:
∫∫f (x, y)dxdy = ∫∫ f (x(u, v), y(u, v))J dudv .
D |
∆ |
Строгое доказательство этой теоремы потребовало бы значительных усилий из-за обилия технических деталей. Мы изложим здесь схему доказательства. Во-первых, оба интеграла в формулировке теоремы существуют, поскольку f (x, y) – непрерывная функция.
Рассмотрим разбиение области ∆ прямыми, параллельными осям u и v. Рассмотрим его часть, имеющую вид прямоугольника с вершинами
(u,v + ∆v) |
(u + ∆u,v + ∆v) |
|
(u,v) |
( |
u + ∆u,v) |
|
|
|
При отображении |
x = x(u, v), y = y(u, v) |
эти точки перейдут, |
соответственно, в точки
Далее, при ∆u → 0, ∆v → 0
10
