
- •Глава 1. Множества и отображения
- •§1.1. Множества и операции над ними
- •1.1.1.Понятие множества
- •1.1.2. Подмножества
- •1.1.3. Операции над множествами
- •§1.2. Декартово произведение множеств, бинарные отношения
- •1.2.1. Декартово произведение множеств
- •1.2.2. Бинарные отношения
- •§1.3. Отображения и их свойства
§1.3. Отображения и их свойства
Определение
1.3.1.Назовём
бинарное отношение
 функциональным,
если для каждого
функциональным,
если для каждого
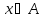 сечение
сечение содержит не более одного элемента.
содержит не более одного элемента.
Определение
1.3.2.Если
отношение
 ,
симметричное к отношению
,
симметричное к отношению ,
также является функциональным, то
отношение
,
также является функциональным, то
отношение называетсявзаимно
однозначным.
называетсявзаимно
однозначным.
Определение
1. 3.3.Если
для каждого
 сечение
сечение содержит ровно один элемент, то
функциональное отношениевсюду
определено.
содержит ровно один элемент, то
функциональное отношениевсюду
определено.
С функциональным отношением непосредственно связано понятие отображения.
Определение1.
3.4.Отображение,
обозначим его
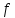 ,
сопоставляет каждому элементу
,
сопоставляет каждому элементу ,
называемомуаргументом
отображения,
для которого сечение
,
называемомуаргументом
отображения,
для которого сечение
 - непустое множество, единственный
элемент
- непустое множество, единственный
элемент подмножества
подмножества множества
множества .
Этот элемент
.
Этот элемент называетсяобразом
элемента
называетсяобразом
элемента
 при отображении
при отображении .
.
Множество
тех элементов
 , для которых существует
, для которых существует , называетсяобластью
определения
отображения
, называетсяобластью
определения
отображения
 .
.
Определение
1. 3.5.Если
отображение
 определено на всём множестве
определено на всём множестве ,
то говорят, что заданоотображение
,
то говорят, что заданоотображение
 в
в
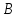 .
.
Определение
1.3.6.Множество
образов элементов
 при отображении
при отображении называетсяобразом
отображения.
Если
называетсяобразом
отображения.
Если
 ,
тообраз
,
тообраз определяется,
как множество образов элементов
определяется,
как множество образов элементов

Определение
1. 3.7.Если
образ совпадает со всем множеством
 ,
то говорят, что заданоотображение
,
то говорят, что заданоотображение на
на
 ,
или что
,
или что
 -сюръективное
отображение,
или сюръекция.
(При этом требование всюду определённости
не является обязательным).
-сюръективное
отображение,
или сюръекция.
(При этом требование всюду определённости
не является обязательным).
Определение
1. 3.8.Если
 ,
то
,
то
 обозначаетпрообраз
множества
обозначаетпрообраз
множества
 ,
т.е. множество тех элементов
,
т.е. множество тех элементов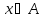 , для которых
, для которых .
.
Отметим очевидные свойства образа и прообраза:

Определение
1.3.9.Если
отношение
 является взаимно однозначным, то
отображение, соответствующее
является взаимно однозначным, то
отображение, соответствующее ,
называетсяобратным
к
,
называетсяобратным
к
 и обозначается
и обозначается .
Если при этом отношение
.
Если при этом отношение всюду определено, то
всюду определено, то называетсяинъективным
отображением,
или инъекцией.
Если, кроме того, отображение
называетсяинъективным
отображением,
или инъекцией.
Если, кроме того, отображение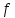 ещё и сюръективно, то оно называетсябиективным
или биекцией.
ещё и сюръективно, то оно называетсябиективным
или биекцией.
Отметим,
что выше мы использовали обозначение
прообраза и
в случаях, когда обратное к
и
в случаях, когда обратное к отображение
отображение не существует. Если же обратное отображение
существует, то прообраз
не существует. Если же обратное отображение
существует, то прообраз можно рассматривать, как образ множества
можно рассматривать, как образ множества при отображении
при отображении .
.
Наиболее
часто встречающимся функциональным
отношением является обычная функция
 ,
определённая на некотором подмножестве
,
определённая на некотором подмножестве числовой прямой, значения которой
образуют множество
числовой прямой, значения которой
образуют множество .
Действительно, эту функциональную
зависимость можно трактовать, как
задание подмножества в множестве
.
Действительно, эту функциональную
зависимость можно трактовать, как
задание подмножества в множестве , в которое входят те пары
, в которое входят те пары , для которых выполнено равенство
, для которых выполнено равенство Изображение этого множества пар на
плоскости носит название графика
функции.
Изображение этого множества пар на
плоскости носит название графика
функции.
