
§2.7. Предельные точки
Определение
2. 7.1.
Окрестностью
 точки
точки
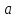 называется любой интервал, содержащий
точку
называется любой интервал, содержащий
точку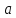 .
Чаще всего рассматривают симметричную
окрестность радиуса
.
Чаще всего рассматривают симметричную
окрестность радиуса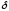 ,
, .Проколотой
окрестностью
точки
a
называется окрестность точки a,
из которой исключена сама точка a,
т.е.
.Проколотой
окрестностью
точки
a
называется окрестность точки a,
из которой исключена сама точка a,
т.е.
 .
.
Определение 2. 7.2. a - предельная точка множества A, если в любой проколотой окрестности точки a есть точки из множества A:
 .
.
В
определении не сказано, что
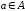 .
В приведенных ниже примерах встретятся
ситуации, и когда предельная точкаа
множества А
принадлежит самому множеству А,
и когда она не принадлежит множеству
А.
.
В приведенных ниже примерах встретятся
ситуации, и когда предельная точкаа
множества А
принадлежит самому множеству А,
и когда она не принадлежит множеству
А.
Пример
1.
Пусть . Любая точка с, не принадлежащая этому
отрезку, не является предельной точкой
(см. рис.1).
. Любая точка с, не принадлежащая этому
отрезку, не является предельной точкой
(см. рис.1).

[(
) ( ] ) a
b (рис.
2)

 можно
указать окрестность точки с, не
пересекающуюся с
можно
указать окрестность точки с, не
пересекающуюся с .
.
Любая
окрестность любой точки
 имеет непустое пересечение с
имеет непустое пересечение с см. рис.2
см. рис.2
Итак, множеством предельных точек отрезка является сам отрезок. Он содержит все свои предельные точки.
Определение 2.7.3. Множество, содержащее все свои предельные точки, называется замкнутым.
 Пример
2.
Пусть
Пример
2.
Пусть
 .
Как и выше, если
.
Как и выше, если ,
то с не является предельной точкой
,
то с не является предельной точкой
 .
.
Но
любая окрестность любой точки
 имеет
непустое пересечение с
имеет
непустое пересечение с
 ,
,

Поэтому
множеством предельных точек интервала
 является отрезок
является отрезок
 .
В этом случае концы
.
В этом случае концы
 этого
отрезка – предельные точки интервала
этого
отрезка – предельные точки интервала ,
не принадлежащие самому интервалу
,
не принадлежащие самому интервалу .
.
Теорема 2.7.1.Если A - бесконечное ограниченное множество, то существует предельная точка множества A.
(Примечание
к формулировке теоремы: слова «бесконечное»
и «ограниченное» не противоречат друг
другу. То, что множество A
ограниченное, означает, что оно
содержится в некоторых границах, т.е.
 .
То,
что множество A
бесконечное, означает, что оно содержит
бесконечно много точек.)
.
То,
что множество A
бесконечное, означает, что оно содержит
бесконечно много точек.)
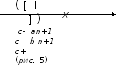 Доказательство.
Рассмотрим
отрезок
Доказательство.
Рассмотрим
отрезок
 .
Разделим его на 2 части. Хотя бы в одну
из половин отрезка входит бесконечное
множество точекA.
Возьмем полученный отрезок
.
Разделим его на 2 части. Хотя бы в одну
из половин отрезка входит бесконечное
множество точекA.
Возьмем полученный отрезок
 и
тоже разделим его на 2 части. Хотя бы
один из полученных отрезков
и
тоже разделим его на 2 части. Хотя бы
один из полученных отрезков тоже
содержит бесконечное множество точек
изA.
Продолжим процесс деления отрезков. В
итоге имеем систему стягивающихся
отрезков. По теоремам (5.3,
5.4)
эта система имеет одну общую ю для всех
отрезков точку с.
Утверждаем, что точка c
- предельная точка множества A.
Выберем произвольную окрестность
тоже
содержит бесконечное множество точек
изA.
Продолжим процесс деления отрезков. В
итоге имеем систему стягивающихся
отрезков. По теоремам (5.3,
5.4)
эта система имеет одну общую ю для всех
отрезков точку с.
Утверждаем, что точка c
- предельная точка множества A.
Выберем произвольную окрестность
 и в ней окрестность
и в ней окрестность
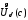 .
После этого возьмем n
такое, чтобы длина отрезка
.
После этого возьмем n
такое, чтобы длина отрезка ,
равная
,
равная ,
оказалась меньше
,
оказалась меньше ,
т.е.
,
т.е.

 .
.
Так
как, очевидно,
 (см.
рис. 5),
и так как
(см.
рис. 5),
и так как
 содержит, по построению, бесконечное
множество
точек из A,
проколотая окрестность
содержит, по построению, бесконечное
множество
точек из A,
проколотая окрестность
 также содержит бесконечное множество
точек изА.
Итак,
доказано, что произвольная окрестность
также содержит бесконечное множество
точек изА.
Итак,
доказано, что произвольная окрестность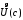 содержит точки изА.
Следовательно, с
–
предельная точка множества А.
содержит точки изА.
Следовательно, с
–
предельная точка множества А.
В дополнение сформулируем и докажем еще одно важное свойство предельных точек.
Теорема
2.7.2. Если
a
– предельная точка множества А, то в
любой проколотой окрестности точки
 содержится
бесконечное множество точек из А.
содержится
бесконечное множество точек из А.
Доказательство.
Рассмотрим
произвольную окрестность
 и
в ней также произвольную
и
в ней также произвольную .
Обозначаем
.
Обозначаем .
В
.
В существует
точка
существует
точка
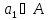 ,
по определению предельной точки. Пусть
,
по определению предельной точки. Пусть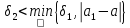 .
. В
.
. В существует
точка
существует
точка
 .
Точка
.
Точка не может совпасть с
не может совпасть с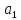 , т.к.
, т.к.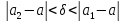 .
Далее полагаем
.
Далее полагаем .
В
.
В существует
точка
существует
точка
 ,
причем
,
причем т.к.
т.к.
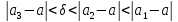 и т.д.
и т.д.
В
итоге получаем бесконечное множество
точек из
 ,
входящих в
,
входящих в
 ,
что и утверждалось.
,
что и утверждалось.
Следствие. Конечное множество не имеет предельных точек.
