
Глава 2. Множество действительных чисел
В начале главы приводятся сведения о натуральных, целых, рациональных числах. Затем рассматриваются действительные числа. Вы можете задать вопрос: а зачем мне изучать теорию действительного числа? В большинстве книг, написанных для экономистов, этот раздел излагается вкратце и, кстати, очень понятно. Чем же хуже я и зачем мне изучать эти аксиомы и странные теоремы? Ответ: Вы не хуже, Вы будете лучше! Потому, что многие современные книги, в частности, написанные для экономистов, охватывают большие фрагменты теорий, понять которые, не зная теории действительного числа, лежащей в основе этих теорий, крайне трудно. В частности, основной инструмент математического анализа – предельный переход, без знания теории действительного числа получится туповатым…
§2.1. Натуральные числа
Натуральное число можно отнести к тем понятиям, которые интуитивно ясны каждому человеку и, разумеется, свойства этих чисел известны из курса средней школы. В этом параграфе мы напомним эти свойства
Сложение натуральных чисел обладает следующими свойствами:
1.
 (ассоциативность, или сочетательный
закон).
(ассоциативность, или сочетательный
закон).
2.
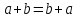 (коммутативность, или переместительный
закон).
(коммутативность, или переместительный
закон).
Для
натуральных чисел
 естественно вводится отношение порядкаменьше
или равно,
обозначаемое
естественно вводится отношение порядкаменьше
или равно,
обозначаемое ,
и для любых чисел
,
и для любых чисел выполняется либо соотношение
выполняется либо соотношение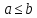 , либо соотношение
, либо соотношение .
.
Отношение порядка обладает такими свойствами:
Если одновременно выполнены соотношения
 и
и ,
то
,
то
Если
 и
и ,
то
,
то .
.Если
 ,
то для всех
,
то для всех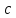 выполняется:
выполняется: +c.
+c.
Умножение натуральных чисел обладает следующими свойствами:
1.
 (ассоциативность, или сочетательный
закон).
(ассоциативность, или сочетательный
закон).
2.
 (коммутативность,
или переместительный закон).
(коммутативность,
или переместительный закон).
3.
Если
 ,
то для всех натуральных
,
то для всех натуральных выполняется: :
выполняется: : c.
c.
4.
 +
+ (дистрибутивность умножения относительно
сложения, или распределительный закон).
(дистрибутивность умножения относительно
сложения, или распределительный закон).
Множество натуральных чисел обозначается N.
Мы не будем подробно останавливаться на позиционных системах счисления, как средствах для изображения чисел. В школе, да и в большинстве вычислений, используется привычная десятичная система счисления. Отметим, однако, что в ряде задач более удобны, например, двоичная или троичная системы. Также в качестве примера изобразим число 100, записанное в десятичной системе, в двоичной системе:1100100
(
так как
 )
)
§ 2.2. Целые числа
Потребности
в вычислениях не позволяют ограничиться
только натуральными числами. Например,
решить простейшее уравнение
 считая
считая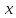 натуральным числом, невозможно.
Естественно дополнить натуральные
числа числом 0 и отрицательными числами.
Число 0 , по определению, обладает
следующими свойствами: для любого числа
натуральным числом, невозможно.
Естественно дополнить натуральные
числа числом 0 и отрицательными числами.
Число 0 , по определению, обладает
следующими свойствами: для любого числа выполняются равенства
выполняются равенства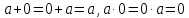 .
.
Нетрудно
доказать, что 0 определяется этими
свойствами единственным образом. .В
самом деле, если мы предположим, что
есть два элемента, обладающих указанными
свойствами, например,
 ,
то получим, что
,
то получим, что .
.
Точно
также, для произвольного натурального
числа
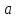 определимпротивоположное
ему целое число
определимпротивоположное
ему целое число
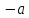 как такое число, что выполняется равенство
как такое число, что выполняется равенство ,
т.е. как решение уравнения
,
т.е. как решение уравнения Натуральные числа, им противоположные
числа и число 0 образуют новое множество,
называемоемножеством
целых чисел. Множество
целых чисел обозначается 𝒁.
Натуральные числа, им противоположные
числа и число 0 образуют новое множество,
называемоемножеством
целых чисел. Множество
целых чисел обозначается 𝒁.
Мы не будем подробно останавливаться на том, как операции сложения и умножения и отношение неравенства переносятся с множества натуральных чисел на множество целых чисел, считая это известным, а просто перечислим свойства целых чисел. Сложение целых чисел обладает следующими свойствами:
1.
 (ассоциативность, или сочетательный
закон).
(ассоциативность, или сочетательный
закон).
2.
 (коммутативность, или переместительный
закон).
(коммутативность, или переместительный
закон).
3.
Существует нейтральный элемент по
сложению, называемый 0, такой, что для
любого целого числа
 выполняются равенства
выполняются равенства .
.
4.
Для произвольного целого числа
 существуетпротивоположное
ему число
существуетпротивоположное
ему число
 такое, что выполняется равенство
такое, что выполняется равенство .
.
Свойство
4 позволяет определить на множестве
целых чисел операцию
вычитания
с помощью равенства .
.
С алгебраической точки зрения эти свойства означают, что множество целых чисел с введённой на нём операцией сложения образует коммутативную группу
Умножение целых чисел обладает следующими свойствами:
 (ассоциативность,
или сочетательный закон).
(ассоциативность,
или сочетательный закон). (коммутативность,
или переместительный закон).
(коммутативность,
или переместительный закон). +
+ (дистрибутивность умножения относительно
сложения, или распределительный закон).
(дистрибутивность умножения относительно
сложения, или распределительный закон).Существует нейтральный элемент по умножению, обозначаемый 1 такой, что
 =
= для любого целого числа
для любого целого числа .
.
С алгебраической точки зрения эти свойства означают, что множество целых чисел с введёнными на нём операциями сложения и умножения образует кольцо.
Для
целых чисел естественно вводится
отношение порядка меньше
или равно,
обозначаемое ,
и для любых целых чисел
,
и для любых целых чисел выполняется либо соотношение
выполняется либо соотношение , либо соотношение
, либо соотношение .
.
Отношение порядка обладает такими свойствами:
Если одновременно выполнены соотношения
 и
и ,
то
,
то
Если
 и
и ,
то
,
то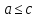 .
.Если
 ,
то для всех
,
то для всех выполняется:
выполняется: +c.
+c.Если
 ,
то для всех натуральных
,
то для всех натуральных выполняется:
выполняется: ,
,
а
для всех отрицательных целых чисел - противоположное неравенство
- противоположное неравенство .
.
Для
целых чисел можно определить понятие
делимости.
Говорят, что целое число
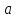 делится
на
целое число
делится
на
целое число без остатка, если существует целое
число
без остатка, если существует целое
число такое, что
такое, что .(Обычно
это обозначают следующим образом:
.(Обычно
это обозначают следующим образом: .)
Число
.)
Число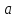 называется делимым, число
называется делимым, число – делителем, число
– делителем, число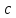 – частным от деления. Если же
– частным от деления. Если же не делится на число
не делится на число без остатка, то его можно единственным
образом представить в виде
без остатка, то его можно единственным
образом представить в виде ,
где
,
где .
.
Зафиксируем
произвольное целое число
 и назовём два целых числа
и назовём два целых числа сравнимыми
по модулю
сравнимыми
по модулю
 (что обозначается
(что обозначается ),
если разность
),
если разность делится на
делится на .
Легко видеть, определённое таким образом
отношение обладает всеми свойствами
отношения эквивалентности. Классы
эквивалентности называютсяклассами
вычетов по модулю
.
Легко видеть, определённое таким образом
отношение обладает всеми свойствами
отношения эквивалентности. Классы
эквивалентности называютсяклассами
вычетов по модулю
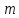 ,
в качестве системы представителей можно
взять всевозможные остатки от деления
на
,
в качестве системы представителей можно
взять всевозможные остатки от деления
на ,
т.е. числа
,
т.е. числа .
Это множество обозначается
.
Это множество обозначается .
.
Сумму
вычетов
 и
и определяем, как остаток от деления на
определяем, как остаток от деления на числа
числа ,произведение
вычетов
,произведение
вычетов
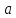 и
и определяем, как остаток от деления на
определяем, как остаток от деления на числа
числа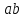 . Операции
над вычетами обладают теми же свойствами,
что и операции над целыми числами.
. Операции
над вычетами обладают теми же свойствами,
что и операции над целыми числами.
