
- •Глава 6. Производные и дифференциалы
- •§ 6.1. Производная и её основные свойства
- •6.1.1. Дифференцируемость функции
- •6.1.2.Производная
- •6.1.3. Касательная к графику функции
- •§ 6.2. Вычисление производных
- •6.2.2. Производные элементарных функций
- •6.2.3. Производная обратной функции
- •6.2.4. Производные обратных тригонометрических функций
- •6.2.5. Производная сложной функции
- •6.2.6. Производная функции, заданной параметрически
- •§6.3. Дифференциал
- •6.3.1.Понятие дифференциала числовой функции
- •6.3.2. Геометрический и механический смысл дифференциала
- •6.3.3. Инвариантность формы первого дифференциала
- •6.3.4.Дифференциал суммы, произведения и частного функций
- •§6.4. Производные и дифференциалы высших порядков
- •6.4.1. Последовательные производные
- •6.4.3. Линейное свойство производных высших порядков
- •6.4.5. Вторая производная функции , заданной параметрически
- •6.4.6. Дифференциалы высших порядков
- •§ 6.5. Эластичность и её свойства
6.4.5. Вторая производная функции , заданной параметрически
Рассмотрим систему уравнений
 (3)
(3)
где
 −
дважды дифференцируемые функции на
некотором промежутке
−
дважды дифференцируемые функции на
некотором промежутке ;
пусть, кроме того, функция
;
пусть, кроме того, функция строго возрастает (или убывает) на
строго возрастает (или убывает) на и ни в одной точке этого промежутка
производная
и ни в одной точке этого промежутка
производная не равна 0. В пункте 6.2.6 доказано, что
в этом случае уравнения (3) задают функцию
не равна 0. В пункте 6.2.6 доказано, что
в этом случае уравнения (3) задают функцию ,
и производная этой функции равна
,
и производная этой функции равна
 =
=
 .
.
Найдём
вторую производную функции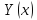 :
:
 =
= .
.
6.4.6. Дифференциалы высших порядков
Напомним,
что если функция дифференцируема в точке
дифференцируема в точке , то
, то
дифференциалом
 в точке
в точке называют линейную форму
называют линейную форму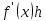 .
.
Аналогично,
если функция дважды дифференцируема в точке
дважды дифференцируема в точке , то
, то
ее
вторым
дифференциалом называют
квадратичную форму
 .
.
При
условии, что существует
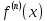 ,n-ым
дифференциалом
,n-ым
дифференциалом

точке
 называется форма
называется форма
Для
 -го
дифференциала
-го
дифференциала в точке
в точке используют обозначение
используют обозначение
 .
В пункте 6.3.1 установлено равенство
.
В пункте 6.3.1 установлено равенство
 используя
используя
которое получим
 =
= (4)
(4)
Форма
(4) записи
 -го
дифференциала не инвариантна уже при
-го
дифференциала не инвариантна уже при .
.
Действительно,
подставляя вместо
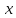 дифференцируемую функцию
дифференцируемую функцию в
левую
в
левую
часть
формулы (4) (при
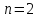 ),
получим
),
получим
 (5)
(5)
а в результате такой же подстановки в правую часть формулы (4), имеем
 (6)
(6)
Правые
части формул (5) и (6) отличаются слагаемым
 ,
которое
,
которое
равно
нулю при условии, что . Это условие выполняется для линейной
. Это условие выполняется для линейной
функции
 .
Отметим, что в этом случае и
.
Отметим, что в этом случае и
поэтому
формула (4) пригодна и в случае линейной
функции
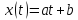 .
.
§ 6.5. Эластичность и её свойства
Определение
6.5.1.
Пусть функция
 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки , дифференцируема в точке
, дифференцируема в точке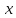 и
и
 .Эластичностью
функции
.Эластичностью
функции в точке
в точке
 называется величина
называется величина
 (1)
(1)
Рассмотрим
причину введения этого понятия. Если
предположить, что
 ,
то можно рассматривать величину
,
то можно рассматривать величину
 ,
(2)
,
(2)
которая
характеризует величину относительного
изменения
 в результате соответствующего
относительного изменения
в результате соответствующего
относительного изменения ;
например, процентное изменение спроса
на товар в результате однопроцентного
изменения цены этого товара. Тогда из
(1) и (2) следует, что
;
например, процентное изменение спроса
на товар в результате однопроцентного
изменения цены этого товара. Тогда из
(1) и (2) следует, что

Если
 ,
то
,
то и
и по теореме о производной сложной функции.
Если
по теореме о производной сложной функции.
Если ,
то
,
то ,
поэтому при
,
поэтому при ,
, .Обе эти формулы можно объединить в одну
:
.Обе эти формулы можно объединить в одну
:
 .
(3)
.
(3)
Теорема 6.5.1.
Если
 ,
–функции,
для которых определены эластичности
,
–функции,
для которых определены эластичности
 и
и
 ,то:
,то:

(4)

2)
Если для функции
 определённой на интервале
определённой на интервале ,
существует обратная функция
,
существует обратная функция ,
причём
,
причём дифференцируема на этом интервале
дифференцируема на этом интервале и ни в одной точке
и ни в одной точке интервала не выполняется равенство
интервала не выполняется равенство ,
то для всех
,
то для всех определены
величины
определены
величины и
и ,
причём
,
причём
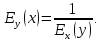 (5)
(5)
Доказательство. По формуле (3)


Равенства (4) доказаны.
Далее,
по теореме о производной обратной
функции
 следовательно,
следовательно,
 .
.
Равенство (5) доказано.
В качестве примера рассмотрим ценовую эластичность спроса.
Пусть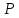 – первоначальная цена товара,
– первоначальная цена товара, –
первоначальное количество получаемой
продукции, т.е. первоначальный спрос,
–
первоначальное количество получаемой
продукции, т.е. первоначальный спрос,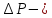 изменение цены,
изменение цены, соответствующее изменение спроса.
Обычно при повышении цены, т.е. при
соответствующее изменение спроса.
Обычно при повышении цены, т.е. при , спрос на товар сокращается, т.е.
, спрос на товар сокращается, т.е. ,
поэтому
,
поэтому
 и,
по теореме о предельном переходе в
неравенствах,
и,
по теореме о предельном переходе в
неравенствах, .
.
Величина эластичности в зависимости от цен представляет собой важную характеристику спроса на товар.
Спрос
является эластичным,
если
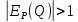 .
При этом уменьшение цен на 1% вызывает
увеличение спроса меньше, чем на 1%.
.
При этом уменьшение цен на 1% вызывает
увеличение спроса меньше, чем на 1%.
При
спросе с единичной
эластичностью,
т.е. когда
 ,
процент увеличения спроса равен проценту
уменьшения цен товара.
,
процент увеличения спроса равен проценту
уменьшения цен товара.
Теорема
6.5.2.
Пусть
 –выручка
от реализации по цене
–выручка
от реализации по цене
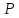 продукции
в объёме
продукции
в объёме .Пусть
.Пусть – дифференцируемая
функция. Если
– дифференцируемая
функция. Если
 ,
т.е. если спрос эластичен, то с ростом
цен выручка
уменьшается,
а с уменьшением цен – возрастает.
,
т.е. если спрос эластичен, то с ростом
цен выручка
уменьшается,
а с уменьшением цен – возрастает.
Если
 ,т.е.
если спрос неэластичен, то с ростом цен
выручка растёт, с уменьшением цен выручка
уменьшается.
,т.е.
если спрос неэластичен, то с ростом цен
выручка растёт, с уменьшением цен выручка
уменьшается.
Если
 ,то
выручка не меняется с изменением цен.
,то
выручка не меняется с изменением цен.

