
- •Глава 6. Производные и дифференциалы
- •§ 6.1. Производная и её основные свойства
- •6.1.1. Дифференцируемость функции
- •6.1.2.Производная
- •6.1.3. Касательная к графику функции
- •§ 6.2. Вычисление производных
- •6.2.2. Производные элементарных функций
- •6.2.3. Производная обратной функции
- •6.2.4. Производные обратных тригонометрических функций
- •6.2.5. Производная сложной функции
- •6.2.6. Производная функции, заданной параметрически
- •§6.3. Дифференциал
- •6.3.1.Понятие дифференциала числовой функции
- •6.3.2. Геометрический и механический смысл дифференциала
- •6.3.3. Инвариантность формы первого дифференциала
- •6.3.4.Дифференциал суммы, произведения и частного функций
- •§6.4. Производные и дифференциалы высших порядков
- •6.4.1. Последовательные производные
- •6.4.3. Линейное свойство производных высших порядков
- •6.4.5. Вторая производная функции , заданной параметрически
- •6.4.6. Дифференциалы высших порядков
- •§ 6.5. Эластичность и её свойства
6.3.4.Дифференциал суммы, произведения и частного функций
В
силу равенства (1) из любой формулы для
производной в точке
 при
при
умножении
на
 получается соответствующая формула
для
получается соответствующая формула
для
дифференциала.
В частности, в точках, где функции
 удовлетворяют
удовлетворяют
условиям теорем о дифференцируемости суммы, произведения или частного
получаем:
 ;
аналогично,
;
аналогично,

 .
.
Отметим,
что если
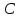 –
постоянная, то
–
постоянная, то

§6.4. Производные и дифференциалы высших порядков
6.4.1. Последовательные производные
Производная
 функции
функции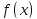 ,
в свою очередь, может иметь производную,
которую называютвторой
производной
(или производной
второго порядка)
функции
,
в свою очередь, может иметь производную,
которую называютвторой
производной
(или производной
второго порядка)
функции
 и обозначают обычно
и обозначают обычно .
Таким образом,
.
Таким образом, .
При этом
.
При этом называютпервой
производной
(или производной
первого порядка)
функции
называютпервой
производной
(или производной
первого порядка)
функции
 .
По индукции определяют (в предположении,
что они существуют) производные следующих
порядков:
.
По индукции определяют (в предположении,
что они существуют) производные следующих
порядков: и
т.д. Если
и
т.д. Если имеет -ю производную (а значит, и
производные всех меньших порядков) во
всех точках некоторого промежутка
имеет -ю производную (а значит, и
производные всех меньших порядков) во
всех точках некоторого промежутка ,
то говорят, что
,
то говорят, что является
является раз
дифференцируемой
на промежутке
раз
дифференцируемой
на промежутке
 .
. -ю
производную функции
-ю
производную функции обозначают
обозначают (в
частности,
(в
частности, ).
При этом удобно бывает считать, что сама
функция равна своей производной нулевого
порядка, т.е.
).
При этом удобно бывает считать, что сама
функция равна своей производной нулевого
порядка, т.е. Функцию
Функцию , имеющую на
, имеющую на производные всех порядков, называютбесконечно
дифференцируемой
на промежутке
производные всех порядков, называютбесконечно
дифференцируемой
на промежутке
 .
Таковы, например, на всем множестве
действительных чисел многочлены,
показательные функции, тригонометрические
функции. Для обозначения порядка
производной, если он невелик, иногда
используют римские цифры. Так,
.
Таковы, например, на всем множестве
действительных чисел многочлены,
показательные функции, тригонометрические
функции. Для обозначения порядка
производной, если он невелик, иногда
используют римские цифры. Так, –
четвертая производная функции
–
четвертая производная функции
Вторая
производная имеет важный механический
смысл. А именно, если при прямолинейном
движении материальная точка в момент
времени
 прошла путь
прошла путь ,
то
,
то представляет
собой скорость движения точки в момент
времени
представляет
собой скорость движения точки в момент
времени ,
а вторая производная
,
а вторая производная это скорость изменения скорости, илиускорение
точки
в момент времени
это скорость изменения скорости, илиускорение
точки
в момент времени
 .
.
Для некоторых бесконечно дифференцируемых функций легко указать формулу для вычисления -ой производной.
6.4.2.
Примеры вычисления производных
 -ого
порядка
-ого
порядка
 .
Поскольку
.
Поскольку
 ,
сделав предположение индукции о том,
что при некотором
,
сделав предположение индукции о том,
что при некотором справедливо равенство
справедливо равенство ,
получим, что
,
получим, что .
Итак, для всех
.
Итак, для всех выполняется равенство
выполняется равенство
 .
.
Отметим,
что в случае
 из этой формулы следует, что
из этой формулы следует, что =
= ,
а при
,
а при
 получаем
получаем =
=
Кроме того, отметим полезную далее формулу
 .
(1)
.
(1)
Доказательство этой формулы точно такое же.
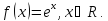 Так
как
Так
как
 для всех
для всех выполняется равенство
выполняется равенство
 (2)
(2)
 Последовательно
находим
Последовательно
находим


 .
.
Полученные
равенства означают, что если
 то
то
 .
Легко проверить, что
.
Легко проверить, что


и
что
 .
.
Следовательно, справедлива формула
 .
(3)
.
(3)
Рассуждая аналогично, получаем, что для
 имеет место формула
имеет место формула
 .
(4)
.
(4)
 Так
как
Так
как
 ,
можно использовать далее формулу (1),
из которой получаем
,
можно использовать далее формулу (1),
из которой получаем
 (5)
(5)
6.4.3. Линейное свойство производных высших порядков
Теорема
6.4.1. Для
любого числа
 ,
любых функций
,
любых функций и
и (x),
имеющих в точке
(x),
имеющих в точке
 производные
производные и
и , и для любых чисел
, и для любых чисел ,
функция
,
функция имеет
в точке
имеет
в точке
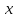 производную
производную .
.
Доказательство. Каждая производная высшего порядка равна производной первого порядка от производной предыдущего порядка. Для производной первого порядка это равенство выполняется по теореме 6.2.1. Применяем метод математической индукции и убеждаемся в справедливости теоремы.
6.4.4. n-я производная произведения
Теорема
6.4.2.(Г. Лейбниц).
Для любых
функций
 и
и (x),
имеющих в точке
(x),
имеющих в точке
 производные
производные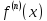 и
и выполнено
равенство:
выполнено
равенство:

 (1)
(1)
Доказательство.
Напомним обозначения: ,
,
 …
…
Используем
метод математической индукции. Для
 утверждение справедливо по теореме
6.2.1:
утверждение справедливо по теореме
6.2.1:
 =
= ,
так
как
,
так
как

Пусть
утверждение теоремы справедливо при
некотором
 ,
и пусть существуют
,
и пусть существуют и
и
 Тогда,
используя теорему 6.2.1,
Тогда,
используя теорему 6.2.1,

 .
(2)
.
(2)
Преобразуем
правую часть формулы (2), замечая, что в
неё входят слагаемые вида
 с
коэффициентами, равными
с
коэффициентами, равными
 Докажем
тождество:
Докажем
тождество:
 Действительно,
Действительно,
 =
=
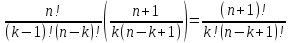 =
=
так что формула (1) верна, если заменить n на n+1 и теорема доказана.
