комплексные числа

Комплексные числа, - расширение поля действительных чисел, обычно обозначается . Любое комплексное число может быть представлено, как формальная сумма , Где и - Действительные числа, - мнимая единица ^[1].

Комплексные числа образуют алгебраически замкнутое поле - это значит, что многочлен степени n с комплексными коэффициентами имеет ровно n комплексных корней ( основная теорема алгебры). Это одна из главных причин широкого применения комплексных чисел в математических исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать много математических моделей, применяемых в математической физике и естественных науках - электротехнике, гидродинамике, картографии, квантовой механике, теории колебаний и многих других.

Представление комплексных чисел

Геометрическое представление

Геометрическая интерпретация комплексных чисел.

Комплексное число можно отождествить с точкой плоскости:

• в декартовой системе координат точка описывается парой координат 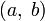или (Алгебраическая форма комплексного числа).

• в полярной системе координат точка описывается длиной вектора (От начала координат до данной точки) и углом 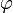между осью абсцисс и данным вектором (тригонометрическая форма комплексного числа).

Для перехода от одной формы записи комплексного числа к другой пользуются формулой:

,

где и - Действительные числа, причем положительное. В такой форме можно подать произвольное комплексное число, отличное от 0.

(Называется модулем числа ) - Это расстояние между точкой и началом координат.

(Называется аргументом числа ) - угол (выраженный в радианах) между правой полуосью оси абсцисс и вышеупомянутым вектором, причем угол отсчитывается против часовой стрелки (а в случае движения по часовой стрелке берется со знаком "минус").

,

,

,

Представление числа в тригонометрической форме единственное с точностью до целого числа полных оборотов, которые можно добавлять к аргументу.

Матричное представление комплексных чисел

Каждому комплексному числу (С действительными и ) Можно поставить в соответствие квадратную матрицу 2-го порядка вида . Такое соответствие задает изоморфизм между системой комплексных чисел и системой матриц такого вида, если сложению, вычитанию и умножению комплексных чисел поставить в соответствие обычные сложения, вычитания и умножения матриц. Легко видеть, что в этом представлены операции комплексного сопряжения соответствует транспонирования матрицы. Настоящая единица представляется как единичная матрица , А мнимая единица - как .

Нетрудно проследить, что действительно вышеуказанные арифметические действия дают соответствующие результаты при выполнении их над числами и над соответствующими матрицами (что и доказывает изоморфность этих структур):

1. , Что соответствует действия .

2. , Что соответствует действия