2. Некоторые дополнительные определения на графах

Многообразие задач моделируемых графами порождает большое количество дополнительных определений и классификаций используемых в теории графов. Познакомимся лишь с небольшой их частью, необходимой нам в моделировании управления проектами.

Ребро e_i и вершина v_j называются инцидентными если вершина v_j является одной из двух вершин, на которых базируется ребро e_i.

Два ребра графа имеющие общую вершину называются смежными. Две вершины графа имеющие общее ребро называются смежными

Путем P(v_a,v_b)={e_i | i=1,…n} между двумя вершинами v_a и v_b графа G(V,E) называется непустое упорядоченное подмножество ребер графа “ведущее” от вершины v_a к v_:. Интуитивно понятный термин “ведущее” означает что:

- e₁ инцидентно v_a, - e_n инцидентно v_b,

- e_iсмежнаe_i-1 | i=2,…n.

Иногда “путь” называют “цепью”.

В приведенном ниже графе (Рисунок 2.1 -2) между вершинами v5 и v7 существует единственный путь состоящий из ребер e5 и e6: P(v5,v7) = {e5,e6}.

На том же графе между вершинами v1 и v3 существует два пути: P₁(v1,v3) = {e2} и P₂(v1,v3) = {e1,e3}.

А вот пути между вершинами v2 и v6 не существует (равно как и между v8 и v1 и многими другими парами).

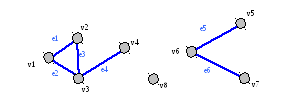
Рисунок 2.1‑2. Пример трехкомпонентного графа

Компонентом связности графа называется подграф - максимально полное подмножество вершин, между каждой парой которых существует путь, и множество ребер их соединяющих. Граф имеющий один компонент связности называется связным.

На приведенном выше примере (Рисунок 2.1 -2) граф имеет три компонента связности: C₁=<{v1,v2,v3,v4},{e1,e2,e3,e4}>; C₂=<{v5,v6,v7},{e5,e6}>; C₃=<{v8}>.

3. Виды графов

В зависимости от семантики задачи рассматривают различные виды графов моделирующих отношения между объектами.

1. Деревья и сети

Деревом называется компонент связности у которого между любыми двумя вершинами существует единственный путь (при этом два пути считаются различными если у них существует хотя бы одно не общее ребро). Граф не являющийся деревом иногда называют сетью.

На приведенном выше примере (Рисунок 2.1 -2) компонент связности C₁ – сеть ибо между вершинами v1 и v3 существует два пути, компонент C_{2 –} дерево, компонент C₃ можно считать вырожденным (состоящим из одной вершины) деревом.

Циклом L на графе называется путь ведущий из любой вершины графа в нее же. Деревья циклов не имеют, для сетей же их наличие характерно. В приведенном выше примере (Рисунок 2.1 -2) только один цикл L={e1,e2,e3}.

2. Ориентированные графы

Граф называется ориентированным если для любого его ребра про пару ее инцидентных вершин известно какая из вершин является началом ребра, а какая ее концом. На ребрах ориентированных графов таким образом появляется направление – от начальной вершины к конечной, которое принято в графических изображениях обозначать стрелкой (Рисунок 2.1 -3). Примером ориентированного графа может служить схема бассейна рек ибо (известно в каком направлении течет каждая из рек его составляющих) или схема электрического сигала (ток течет от источников к приемникам). Немного позднее будет показано, что и графы моделирующие управление проектом являются ориентированными.

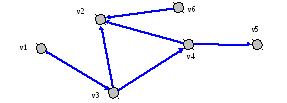
Рисунок 2.1‑3. Пример ориентированного графа.

Для каждой вершины ориентированного графа все инцидентные ребра можно разделить на исходящие (началом которых является данная вершина) и на входящие (концом которых является данная вершина).

Для ориентированного графа принято различать корневые вершины и терминальные вершины. Корневой вершиной называется вершина графа, все инцидентные ребра которой являются исходящими. Терминальной вершиной называется вершина графа, все инцидентные ребра которой являются входящими. На приведенном выше графе вершины v1 и v6 являются корневыми, а v2 и v5 – терминальными.

Граф называется неориентированным если ни для одного его ребра направление не задано. Схема метрополитена – это пример неориентированного графа.

Существуют и задачи, в которых рассматриваются частично ориентированные графы. В них направление задано не для всех ребер. Примером такого графа может служить дорожная схема, на которой у некоторых участков установлено одностороннее движение.