Некоторые азы теории
В отличие от других программных продуктов входящих в состав MS Office, MS Project является продуктом с четко выраженной профессиональной ориентацией. Являясь инструментом менеджера, MS Project требует, даже в начальной стадии обучения, наличия определенных профессиональных знаний в области управления проекта.
Рассмотрению начального ряда связанных определений в проблематике моделирования проекта посвящен этот раздел.
Теория графов
Возникший в XVIII веке интерес к изучению графов прошел эволюцию от небольшого “развлекательного” раздела математики, основу которому положили несколько работ Л. Эйлера, до современной теории графов, имеющей большое практическое применение в различных областях человеческой деятельности.
Первой задачей, с которой Эйлер начал свою работу о графах была “задача о Кенигсбергских мостах”. Необходимо было в условиях города разрезанного рекой на четыре части и имеющего семь мостов найти путь начинающийся и кончающийся в одной точке и проходящей по каждому мосту равно один раз. Не менее известной является и другая классическая задача теории графов - “задача коммивояжера”. Нужно посетить n городов, расстояния между которыми известны, за минимальное время вернувшись в исходную точку. От этих задач и пошло одно из основных применений теории графов, которое принято называть “транспортными задачами”. Поставьте себя на место диспетчера перевозок бетона в городе имеющем несколько бетонных узлов – производителей и множество строек – потребителей. Задача оптимального планирования перевозок – типичный пример транспортной задачи.
Следующая большая область применения теории графов – анализ и проектирование электрических цепей. Работы , Г. Кирхгофа именно в этой области существенно продвинули построение теории графов.
Задачи проектирования и обслуживания сетей (от водопроводных до компьютерных) – это тоже задачи теории графов.
Теория графов имеет тесные связи с такими разделами математики как теория автоматов, теория кодирования, топология, исследование операций и другими.
Самостоятельное значение теория графов имеет в программировании и информатике. Объясняется это тем, что граф представляет собой один из наиболее универсальных, развитых и имеющих графическую интерпретацию средств представления отношений между объектами.
Ну и, наконец, теория графов оказала прямое влияние на становление современных методов планирования. Последнее обстоятельство и побуждает нас заняться здесь изучением некоторых основных понятий и методов этой теории.
Определение графа
Под графом (graph) понимают совокупность вершин (vertices) и соединяющих их ребер (edges). Вершины в графе часто называет узлами (nodes) – эти термины эквивалентны.
Более строго: графом G(V,E) называется совокупность двух множеств – множества V (множество вершин) и множества E (множество ребер), связанных следующим отношением. Каждый элемент множества Е определяет отношение (соединяет) между двумя элементами множества V.
Итак:
G(V,E) = <V,E>, E={e=(v1,v2)}
В качестве первого примера графа и его графической иллюстрации рассмотрим фрагмент схемы метрополитена. Этот фрагмент содержит 6 станций и 7 перегонов. Соответствующий ему граф (Рисунок 2.1 -1):
G(V,E)=<V,E>, V={v1,v2,v3,v4,v5,v6}, E={e1=(v2,v4),e2=(v4,v5),e3=(v4,v6),e4=(v1,v5),e5=(v2,v1), e6=(v1,v3), e7=(v2,v5)}
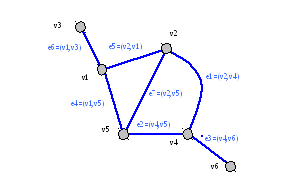
Рисунок 2.1‑1. Пример графа. Фрагмент схемы метрополитена.
Обратим внимание на несколько аспектов определения графа.
Множество вершин не может быть пустым. А вот множество ребер – может и в этом случае такой граф называют “нуль-графом”.
Множество ребер неупорядочено, то есть между ребрами нет дополнительных отношений
В определении ничего не говорится о дополнительных свойствах вершин и ребер и, в частности, нет понятия “координат узлов”. Поэтому расположение узлов (станций метрополитена) в той или иной точке на приведенном выше рисунке условно. Это именно схема, а не выполненная в масштабе карта.