2. Сетевой график и календарное планирование

Рассмотренная в предыдущем разделе модель сетевого графика не дает ответ на задачу календарного планирования – когда должна начаться каждая из задач проекта, какие ресурсы и когда должны привлекаться. Для того чтобы наделить сетевой график такими возможностями необходимо лишь привязать сетевой график к временной шкале и определить ресурсы потребные для исполнения каждой из представленных в графике работ. Сетевые графики наделенные такими свойствами называют календарными сетевыми графиками.

Для привязки сетевого графика к временной шкале основополагающим является выбор типа привязки. Различаются два типа проектов:

• c заданной датой начала проекта,

• с заданной датой окончания проекта.

В проектах с заданной датой начала каждую работу начинают как можно быстрее. В проектах с заданной датой начала проекта каждую работу начинают как можно позже. Объясняется это обстоятельство лишь одним – необходимо минимизировать срок окупаемости путем скорейшего окончания проекта (в проекте с заданной датой начала) либо путем максимально поздних затрат (в проекте с заданной датой окончания).

Итак, для привязки сетевого графика к временной оси достаточно указать тип проекта и соответствующую дату начала или окончания проекта. Дата начала и окончания каждой работы после этого становится детерминированной (вычисляемой). Возможные вариации этих вычислений рассматриваются в следующем разделе.

Назначение ресурсов (людских и финансовых ресурсов, оборудования, расходных материалов) потребных для исполнения каждой задачи в совокупности с определенными сроками исполнения работ не только позволяет рассчитать календарные графики использования ресурсов, но и ставит еще одну расчетную задачу перед менеджером проекта. В условиях ограниченных ресурсов необходимо осуществлять контроль за тем, чтобы в любой момент исполнения проекта суммарное количество каждого используемого в этот момент ресурса не превысило установленное ограничение. Процесс такого контроля, включающий средства изменения сроков исполнения работ и переброски ресурсов как средства борьбы с обнаруженными нарушениями, называется выравниванием ресурсов (resource leveling).

3. Расчеты временных показателей на сетевых графиках

Любая разработанная модель позволяет анализировать поведение моделируемого объекта в рамках адекватности модели. Рассмотрим что же позволяет оценить сетевой график в процессе управления проектом.

1. Критический путь и продолжительность проекта.

Попробуем оценить продолжительность проектов приведенного на рисунке 2.2-9 в ПЕРТ-представлении (число указанное рядом с наименованием работы означает продолжительность работы).

Введем понятие продолжительность пути на сетевом графике как суммы продолжительности работ его составляющих.

Рассмотрим все пути ведущие на сетевом графике из события-начала проекта в событие – окончание проекта. На приведенном на рисунке 2.2-9 примере сетевого графика таковых насчитывается шесть:

D(A-B-C-G) = D_A+ D_B+ D_C+ D_G = 3 + 5 + 2 +4 = 14

D(A-D-F-G) = D_A+ D_D+ D_F+ D_G = 3 + 4 + 3 +4 = 14

D(A-D-H-J) = D_A+ D_D+ D_H+ D_J = 3 + 4 + 1 +5 = 13

D(A-E-F-G) = D_A+ D_E+ D_F+ D_G = 3 + 5 + 3 +4 = 15

D(A-E-H-J) = D_A+ D_E+ D_H+ D_J = 3 + 5 + 1 +5 = 14

D(K-J) = D_K + D_J = 7 + 5 = 12

Поскольку проект заканчивается лишь с выполнением всех работ, то его продолжительность определяет продолжительность самого длинного из рассмотренных путей. Значимость пути максимальной продолжительности в проекте подчеркивается данным ему названием – критический путь. Путей с максимальной одинаковой продолжительностью может быть несколько ( критических путей на сетевом графике может быть несколько).

В рассматриваемом примере критическим путем является путь A-E-F-G, а продолжительность проекта равна 15. На рисунке 2.2-9 он помечен линией двойной ширины.

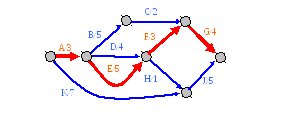
Рисунок 2.2‑9. Продолжительность проекта равна 15.

Для того чтобы лучше понять значение критического пути и возможные метаморфозы связанные с изменением проекта рассмотрим теперь задачу снижения продолжительности проекта. Ни один проект не желает умещаться в прокрустово ложе отведенных сроков, поэтому эта задача для менеджера проекта является едва ли не самой распространенной. Сейчас оставим в стороне такой прием как распараллеливание работ и будем оперировать только продолжительностью отдельных работ в условиях неограниченных ресурсов. Естественно что в этом процессе необходимо минимизировать производимое “сжатие”работ, ибо сокращение продолжительности работы приводит, как правило, к излишним затратам (вспомните соотношение цен при “обычном” и “срочном” исполнении заказа в каком-нибудь предприятии по обслуживанию).

Поставим задачу уменьшения продолжительности проекта рисунка 2.2-9 с 15 до 13 единиц. Бесполезно уменьшать продолжительность любой работы не лежащей на критическом пути, ибо это оставит критический путь, а, следовательно, и продолжительность проекта без изменения. У каких же работ из четырех работ критического пути снижать продолжительность? Безусловно семантика работ, в первую очередь, должна подсказать ответ на этот вопрос. Но в нашей абстрактной модели смысл работ скрыт и кроме топологии (структуры) графа и продолжительности работ ничего не известно. Остается прибегнуть либо к произвольному выбору, либо выбрать работу (одну или несколько), для которой снижение продолжительности в процентном отношении будет минимально. Примем решение сократить продолжительность работы E на две единицы. Теперь продолжительность E будет равна 3. Получим график приведенный на рисунке 2.2-10.

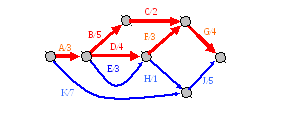
Рисунок 2.2‑10. Продолжительность проекта равна 14.

Проанализировав новый вариант сетевого графика, можно сказать что желаемого результата не достигнуто. Продолжительность проекта стала равна 14, ибо теперь критических путей с продолжительностью 14 два: A-B-C-G и A-D-F-G. Для достижения поставленной цели (уменьшить продолжительность проекта до 13) придется выбирать работы из новых критических путей. Заметим что сокращение работы A или работы G на одну единицу позволит сократить продолжительность сразу обоих критических путей, т.к. обе этих работы принадлежат к общей части критических путей. Предпочтительнее в данном случае выбрать работу A – ведь она принадлежала единственному критическому пути исходного графика. Сокращение ее продолжительности на единицу даст возможность уменьшить исходную продолжительность E всего на 1 (а не на 2) с тем чтобы привести продолжительность исходного критического пути A-E-F-G к 13. Итак, сокращаем продолжительность работы A на единицу, а продолжительность работы E увеличиваем на 1 (отказываемся от ненужных затрат). Получаем вариант графика приведенный на рисунке 2.2-11. Поставленная цель достигнута.

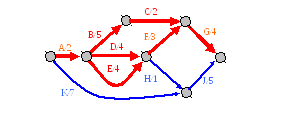
Рисунок 2.2‑10. Продолжительность проекта равна 13.