4.4.2.Вычисление пределов , ,

Эти пределы далее будут использованы при вычислении производных основных элементарных функций. Вновь подчеркнём, что отвечая на экзамене вопрос о вычислении этих пределов, нельзя пользоваться правилами Лопиталя или формулой Тейлора. Разумеется, они дадут верный ответ, но их применение требует знания производных функций, стоящих в числителях этих дробей. А для вычисления этих производных, как отмечено выше, требуется знать эти самые пределы. Поэтому получится не доказательство, а порочный логический круг.

Теорема4.8. =1, =,

=.

Доказательство. В теореме 3.8.2 мы установили, что . Рассмотрим левую часть этого равенства и преобразуем её так:. По непрерывности показательной функции (а именно: непрерывность функции означает, что ) получаем , т. е..

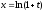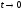Далее рассмотрим предел и сделаем в нём замену переменной(это – монотонная замена и теорема 4.1.3 о пределе сложной функции применима). Прии, и наоборот, притакже.

Поэтому

,

по доказанному выше.

Для предела имеем

.

Рассмотрим . Обозначим, т. е.. Тогда, и припеременная, и наоборот, припеременная.Наш предел примет вид .

Это преобразование законное, т. к. при и, поэтому. Далее используем доказанное в первом пункте равенство. Таким образом, искомый предел равен

.

Запишем найденные предельные соотношения с помощью символа. Равенство

означает, что ,при или что ,

.

Равенство означает, что,

.

Аналогично, ,

.

(Кстати, равенство означает, что при

).