Глава 18

Глава 18. Собственные интегралы, зависящие от параметра

§18.1.Предельный переход под знаком интеграла

Пусть функция определена на прямоугольнике , заданном неравенствами: , .

Пусть для любого функция интегрируема по (по Риману).

Определение 18.1. Интеграл называется собственным интегралом, зависящим от параметра , а отрезок называется множеством значений параметра .

Это определение можно расширить, рассматривая вместо отрезка любое подмножество вещественной оси , например, интервал, полуинтервал, луч, всю , проколотую окрестность точки и т.д.

Теорема 18.1. Пусть непрерывна на прямоугольнике . Тогда непрерывна на отрезке .

►Прямоугольник - замкнут и ограничен, поэтому является компактом. По теореме Кантора, функция непрерывная на компакте , равномерно непрерывна на . Поэтому для любого существует число, такое, что для любых точек удовлетворяющих условиям , выполняется неравенство:

.

Пусть , тогда, согласно предыдущему неравенству, в котором для любого и любого выбраны

выполняется неравенство .

Тогда .

Следовательно, при имеем: , т.е. .

Так как - произвольная точка , теорема доказана. ◄

Обобщим доказанную теорему.

Теорема 18.2. Пусть , непрерывны на отрезке и удовлетворяют неравенствам .

Тогда - непрерывная на функция.

►Прежде всего, отметим, что можно рассматривать, как интеграл от параметра, определённый для функции

Рассмотрим

.

Пусть числа , те же, что и в предыдущей теореме (т.е. если , , то ). Тогда

Далее, непрерывная на компакте функция ограничена. Пусть

. Тогда получаем неравенство

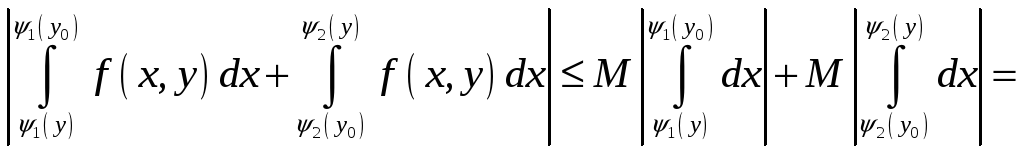
при .

Поэтому при выполняется неравенство

из которого следует, что при .◄

Доказанные теоремы допускают равносильную переформулировку:

.

Введём важное для дальнейшего определение:

Определение 18.2. Семейство функций ( - параметр семейства, ) равномерно ( относительно )стремится к предельной функции при , если

.

Теорема 18.3. Если при фиксированном непрерывна по , и при стремится к предельной функции равномерно (относительно ), то

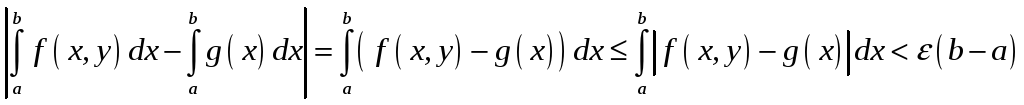► при , что и требовалось. ◄

Пример . Найти

( - непрерывна) .

Пример.

(, , непрерывны)=.

§18.2.Дифференцирование под знаком интеграла. Правило Лейбница

Теорема 18.4. (Правило Лейбница). Пусть непрерывна на . Тогда дифференцируема на , причём

(В концах отрезка производные односторонние).

►Пусть , , . Тогда

Подынтегральная функция непрерывна по , значит, интегрируема. По теореме Лагранжа получаем:

,

По условию, и, значит, равномерно непрерывна на ; поэтому для любого существует такое, что из , следует, что

При , , получаем, что если , то для любого

,

откуда

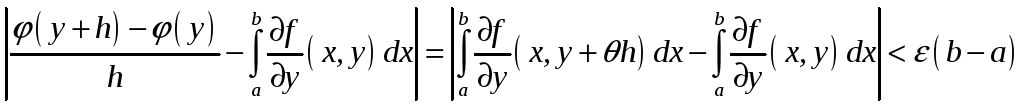
и .◄

Теорема 18.5. В условиях предыдущей теоремы пусть , , где , дифференцируемы на . Тогда

►

(обозначим , , )

Дословно повторяя рассуждения предыдущей теоремы, получим, что при

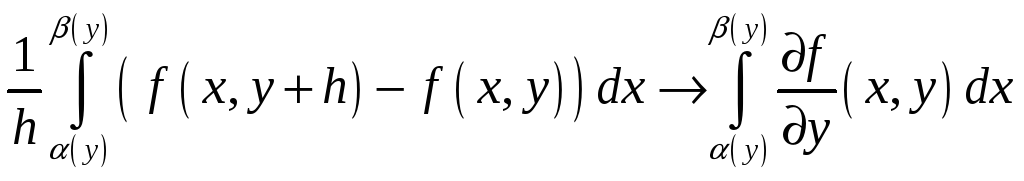
Далее, по теореме о среднем 15.17, ввиду непрерывности подынтегральной функции

()

При получаем

.◄

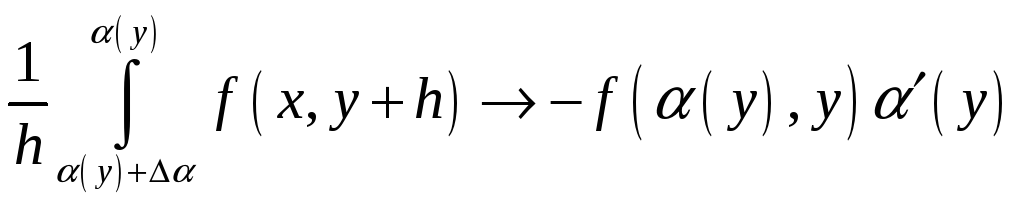
Пример.

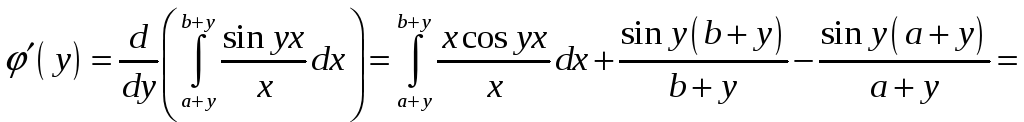
§18.3. Интегрирование по параметру под знаком собственного интеграла

Теорема 18.6. Пусть . Тогда существуют и равны интегралы

► Обозначим первый из этих интегралов , второй - .

Положим , , .

Докажем, что эта функция непрерывна по совокупности переменных.

Оба слагаемых стремятся к 0, первое по непрерывности , при .

по свойству интеграла с переменным верхним пределом, поэтому для

имеем, по правилу Лейбница,

(это обозначение).

Но для , по теореме Ньютона-Лейбница

где

Итак, ,. По критерию постоянства функции, с учётом равенств , для всех выполняется равенство. При получаем утверждение теоремы.◄