Алгоритм метода ветвей и границ

Шаг 1. Строятся вершины первого уровня. Для каждой вершины подсчитывается оценка нижней (верхней) границы. Ветвится вершина, которой соответствует лучшая (минимальная или максимальная) оценка.

Шаг 2. Для всех вершин -го уровня () подсчитывается оценка. Ветвится та из висячих вершин уровня , которой соответствует лучшая (минимальная или максимальная) оценка.

Шаг 3. Действия шага 2 повторяются до тех пор, пока не будет получено точное решение на последнем уровне. Для него подсчитывается точное значение . Если это значение не хуже оценок оставшихся висячих вершин, то найдено оптимальное решение. Если это значение строго лучше, то оптимальное решение единственно. Если значение функции для вершин последнего уровня не лучше значения оценок оставшихся висячих вершин, то переходят на шаг 2.

Метод ветвей и границ не гарантирует того, что в ходе решения задачи не будет произведен полный перебор.

Для практической реализации метода ветвей и границ применительно к задаче коммивояжера укажем прием определения нижних границ подмножеств и разбиения множества маршрутов на подмножества (ветвление).

Для того чтобы найти нижнюю границу воспользуемся следующим соображением: если к элементам любого ряда матрицы задачи коммивояжера (строке или столбцу) прибавить или вычесть из них некоторое число, то от этого оптимальность плана не изменится. Длина же любого маршрута коммивояжера изменится на данную величину.

Вычтем из каждой строки число, равное минимальному элементу этой строки. Вычтем из каждого столбца число, равное минимальному элементу этого столбца. Полученная матрица называется приведенной по строкам и столбцам. Сумма всех вычтенных чисел называется константой приведения.

Константу приведения следует выбирать в качестве нижней границы длины маршрутов.

Разбиение множества маршрутов на подмножества

Для выделения претендентов на включение во множество дуг, по которым производится ветвление, рассмотрим в приведенной матрице все элементы, равные нулю. Найдем степени Θ_ij нулевых элементов этой матрицы. Степень нулевого элемента Θ_ij равна сумме минимального элемента в строке i и минимального элемента в столбце j (при выборе этих минимумов c_ij – не учитывается). С наибольшей вероятностью искомому маршруту принадлежат дуги с максимальной степенью нуля.

Для получения платежной матрицы маршрутов, включающей дугу (i, j) вычеркиваем в матрице строку i и столбец j, а чтобы не допустить образования цикла в маршруте, заменяем элемент, замыкающий текущую цепочку на бесконечность.

Множество маршрутов, не включающих дугу (i, j) получаем путем замены элемента c_ij на бесконечность.

Пример (г.И. Просветов, 2009, стр. 44)

Решим задачу коммивояжера для пяти пунктов.

Расстояния между населенными пунктами заданы с помощью матрицы

,

где - длина пути от пункта i до пункта j.

На каждом шаге ребро либо включается в ответ (обозначение ), либо не включается в ответ (обозначение ).

Шаг 1. Нахождение константы приведения.

Находим минимальный элемент в каждой строке и вычитаем его из всех элементов этой строки. В полученной матрице находим минимальный элемент в каждом столбце и вычитаем его из каждого элемента соответствующего столбца.

Найденные минимумы в строке и столбце называются константами приведения строки или столбца соответственно. Сумма всех найденных минимумов равна 18 – константа приведения матрицы. Она дает оценку снизу на данном шаге длины маршрута.

Шаг 2. Определение дуги, исключение которой максимально увеличивает оценку, полученную на предыдущем шаге.

С этой целью заменяем поочередно каждый из нулей на и вычисляем сумму наименьших элементов в строке и столбце, содержащих этот новый элемент .

Элемент имеет наибольшую сумму. Поэтому все множество маршрутов распадается на два класса: (не содержат дугу ) и (содержат дугу ).

Шаг 3. Определение множества дуг для дальнейшего ветвления.

Рассмотрим множество . Исключение дуги проводится с помощью замены элемента на :

.

В полученной матрице нужно определить сумму констант приведения:

Нижняя граница множества , где 18 – оценка предыдущего шага, 3 – оценка текущего шага.

Рассмотрим множество . Включение дуги проводится с помощью исключения 1-й строки (в множестве из пункта 1 мы идем только в пункт 3) и 3-го столбца (в множестве в пункт 3 мы можем попасть только из пункта 1). Элемент (3,1) заменяем на (исключаем возможность возвращения, зацикливания, образования негамильтонова цикла):

.

Нижняя граница множества , где 18 – оценка предыдущего шага, 1 – оценка текущего шага. Числа над матрицей суть номера столбцов, числа перед матрицей – номера строк.

Так как , то дальше ветвим множество .

Для матрицы

определим дугу, исключение которой максимально увеличило бы полученную оценку . Для этого заменяем поочередно каждый из нулей на и вычисляем сумму наименьших элементов в строке и столбце, содержащих этот новый элемент :

Для элемента эта сумма наибольшая. Поэтому все множество маршрутов распадается на два класса: (не содержит дугу ) и (содержит дугу ).

Рассмотрим множество . Исключение дуги проводится с помощью замены элемента на :

.

Определим в полученной матрице ее константу приведения:

.

Нижняя граница .

Рассмотрим множество . Включение дуги проводится с помощью исключения 2-й строки, 5-го столбца и замены элемента (5,2) на :

В полученной матрице

нужно определить константу приведения.

.

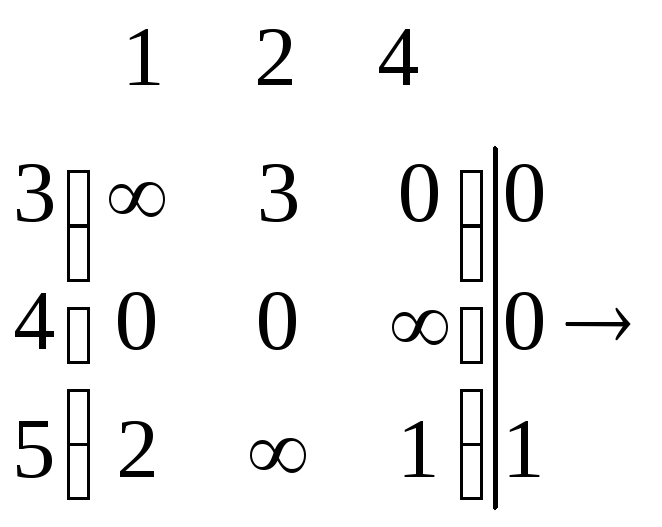
Нижняя граница . Поэтому дальше ветвим множество .

Для матрицы

определим дугу, исключение которой максимально увеличивает оценку . С этой целью заменяем поочередно нули на и вычисляем сумму наименьших элементов в строке и столбце, содержащих этот новый элемент . Полученные суммы указываются в качестве верхних индексов нулей:

.

Для элементов (3,4) и (4,2) эта сумма наибольшая. Выберем любой из них. Пусть это будет элемент (4,2). В этом случае все множество маршрутов распадается на два класса: (маршруты содержат дугу (4,2)) и (маршруты не содержат дугу (4,2)).

Рассмотрим множество . Исключение дуги (4,2) проводится с помощью замены элемента (4,2) на :

.

Определим в полученной матрице сумму констант приведения:

.

Получаем .

Рассмотрим множество . Включение дуги (4,2) производится за счет исключения 4-й строки и 2-го столбца. Элемент (2,4) в матрице отсутствует, поэтому нет угрозы зацикливания.

Для полученной матрицы определяем ее константу приведения. Очевидно, что она равна 1. Нижняя граница множества равна . Поэтому в дальнейшем ветвим множество .

Для этого в матрице

надо так выбрать нули, чтобы в каждой строке и в каждом столбце был ровно один отмеченный нуль. Это элементы (3,4) и (5,1). Именно эти дуги и нужно добавить в множество маршрутов : ответом в задаче является множество . Минимальная длина маршрута 21 (оценка, полученная на предыдущем шаге, не меняется). Маршрут, являющийся решением, выглядит следующим образом:

.

В.В. Водянова