
- •Механический смысл двойного интеграла
- •Основные свойства двойных интегралов
- •Вычисление двойных интегралов в декартовых координатах
- •Замена переменных в двойном интеграле
- •Формула замены переменных в двойном интеграле
- •Переход в двойном интеграле к полярным координатам
- •Применение двойных интегралов
- •Решение задач
- •Вопросы для самопроверки по теме 6.1
- •6.2. Криволинейные интегралы первого рода
- •Определение криволинейного интеграла первого рода и его основные свойства
- •Механический смысл криволинейного интеграла первого рода
- •Достаточные условия существования криволинейного интеграла первого рода
- •Основные свойства криволинейных интегралов первого рода
- •Вычисление криволинейных интегралов первого рода
- •Решение задач
- •Вопросы для самопроверки по теме 6.2
- •6.3. Криволинейные интегралы второго рода
- •Определение криволинейного интеграла второго рода и его основные свойства
- •Достаточные условия существования криволинейных интегралов второго рода
- •Механический смысл криволинейного интеграла второго рода
- •Свойства криволинейных интегралов второго рода
- •Связь между криволинейными интегралами первого и второго родов
- •Вычисление криволинейных интегралов второго рода
- •Формула Грина
- •Связь двойного интеграла с криволинейным
- •Условия независимости криволинейных интегралов от пути интегрирования
- •Решение задач
- •Вопросы для самопроверки по теме 6.3
- •Заключение
- •3.3. Глоссарий
Основные свойства криволинейных интегралов первого рода
Перечислим основные свойства, предполагая, что все встречающиеся ниже функции и кривые удовлетворяют условиям теоремы 6.4. Эти свойства выводятся непосредственно из определения криволинейного интеграла аналогично тому, как доказываются свойства определенного интеграла.
1.  ,
т.е. значение
криволинейного интеграла не зависит
от направления кривой.
,
т.е. значение
криволинейного интеграла не зависит
от направления кривой.
2.  .
.
3.  .
.
Из свойств 2 и 3 следует свойство линейности криволинейного интеграла
 .
.
4. Свойство аддитивности.
Если кривая АВ разбита точкой С на две части АС и СВ, то
 .
.
Если
 для всех точекМ
кривой АВ,
то
для всех точекМ
кривой АВ,
то
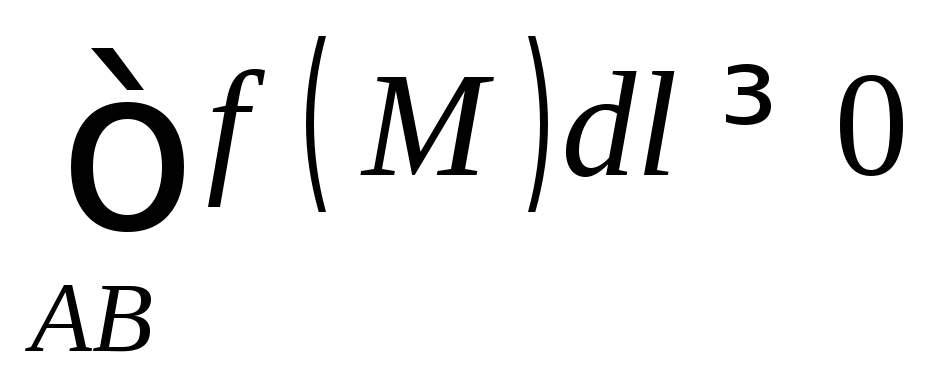 .
.
Если
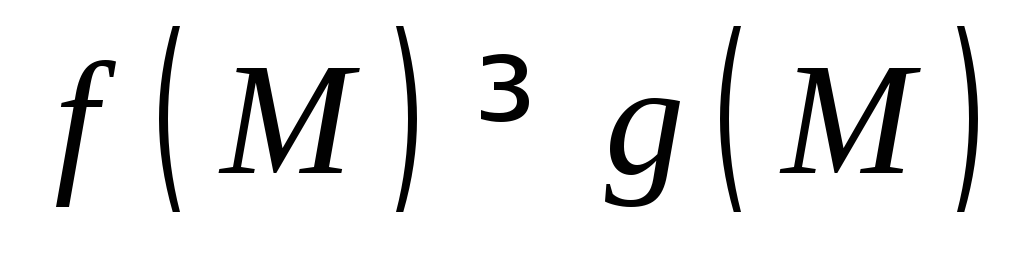 для всех
точек М
кривой АВ,
то
для всех
точек М
кривой АВ,
то

7.

8.
 ,
где
,
где![]() - длина кривойАВ.
- длина кривойАВ.
9. Теорема о среднем.
Если
функция
![]() непрерывна
на кривой АВ,
то на этой
кривой найдется хотя бы одна такая точка
непрерывна
на кривой АВ,
то на этой
кривой найдется хотя бы одна такая точка
![]() ,
что
,
что

Вычисление криволинейных интегралов первого рода
Вычисление криволинейных интегралов первого рода сводится к вычислению определенных интегралов. Приведем правила вычисления интегралов первого рода.
1.
Пусть кривая АВ
- плоская и
задается уравнением
![]() ,
,![]() ,
где
,
где
![]() - функция,
непрерывно дифференцируемая на
- функция,
непрерывно дифференцируемая на
![]() ,
a точкамА и
В соответствуют
значения
,
a точкамА и
В соответствуют
значения
![]() и
и
![]() соответственно.
Тогда
соответственно.
Тогда
 (6.14)
(6.14)
Выражение
![]() называется
дифференциалом
длины дуги кривой.
называется
дифференциалом
длины дуги кривой.
Если
кривая АВ -
плоская и
задается уравнением
![]() ,
,![]() ,
где
,
где
![]() - функция,
непрерывно дифференцируемая на
- функция,
непрерывно дифференцируемая на
![]() ,
а точкам А
и В
соответствуют
значения
,
а точкам А
и В
соответствуют
значения
![]() и
и
![]() ,
то получим формулу, аналогичную формуле
(6.14):
,
то получим формулу, аналогичную формуле
(6.14):
 (6.15)
(6.15)
В
этом случае дифференциал длины дуги
кривой
![]()
2. Пусть кривая АВ - плоская и задается параметрическими уравнениями
![]()
где
![]() и
и
![]() - функции,
непрерывно дифференцируемые на
- функции,
непрерывно дифференцируемые на
![]() ,
a точкам А
и
В соответствуют
значения параметра
,
a точкам А
и
В соответствуют
значения параметра
![]() и
и
![]() .
.
 (6.16)
(6.16)
Дифференциал
длины дуги кривой в этом случае
![]()
3. Пусть АВ - пространственная кривая и задается параметрическими уравнениями
![]()
где
![]() - функции,
непрерывно дифференцируемые на
- функции,
непрерывно дифференцируемые на
![]() ,
а точкамА и
В соответствуют
значения параметра
,
а точкамА и
В соответствуют
значения параметра
![]() и
и
![]() .
Тогда
.
Тогда
 Дифференциал
длины дуги кривой
Дифференциал
длины дуги кривой
![]()
4. Если различные участки кривой АВ задаются различными формулами, то нужно воспользоваться свойством аддитивности интеграла, т.е. разбить кривую на соответствующее число частей, вычислить интегралы по этим частям и просуммировать.
Пример
6.4. Вычислить
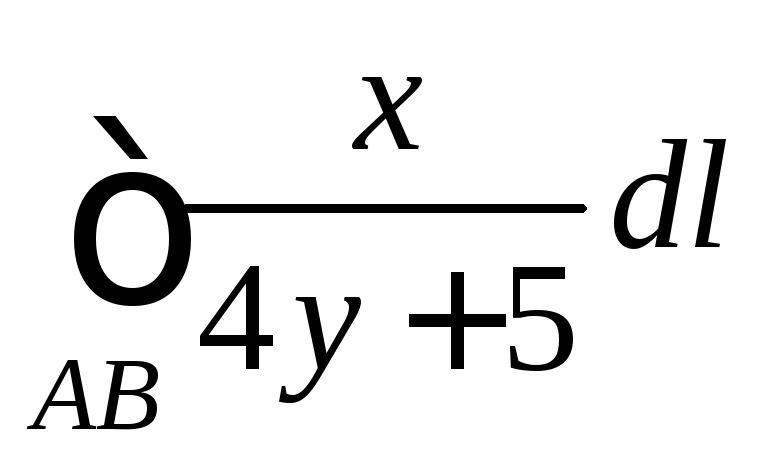 вдоль параболы
вдоль параболы![]() от точки
от точки![]() до точки
до точки![]() .
.
Решение. Воспользуемся формулой (6.14):
 Пример
6.5. Вычислить
Пример
6.5. Вычислить
 вдоль первого витка винтовой линии:
вдоль первого витка винтовой линии:![]()
Решение. Вычислим сначала dl :
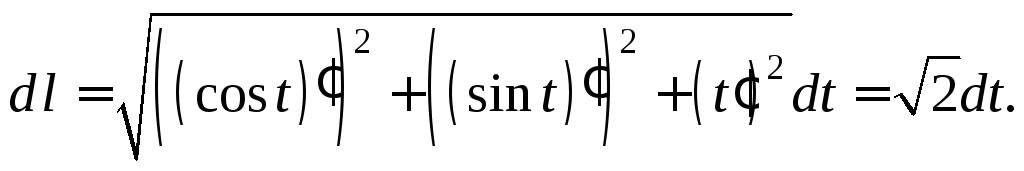
Тогда, используя формулу (6.17), получаем

Решение задач
Задача
6.9.
Найти
дифференциал
![]() длины дуги кривой
длины дуги кривой .
.
Решение.
Учитывая, что
 ,
получаем
,
получаем
![]() .
.
Задача
6.10.
Найти
дифференциал
![]() длины дуги кривой
длины дуги кривой![]() .
.
Решение.
В случае,
если кривая задается параметрически,
то
![]()
Вычислим
![]() и
и![]() .
.![]() .
Тогда
.
Тогда
![]() .
.
Задача
6.11.
Вычислить
 ,
где
,
где![]() - дуга параболы
- дуга параболы![]() от точки
от точки![]() до точки
до точки![]() .
.
Решение.
Воспользуемся формулой (6.14), вычислив
предварительно
![]() .
.
 .
Тогда
.
Тогда
 .
.
Задача
6.12. Вычислить
![]() ,
где
,
где![]() - дуга кривой
- дуга кривой .
.
Воспользуемся
формулой (6.15), вычислив предварительно
![]() .
.![]() .
Тогда
.
Тогда

Следовательно,

Задача
6.13. Найти
массу
![]() дуги материальной кривой
дуги материальной кривой![]() между точками
между точками![]() и
и![]() ,
если плотность вещества
,
если плотность вещества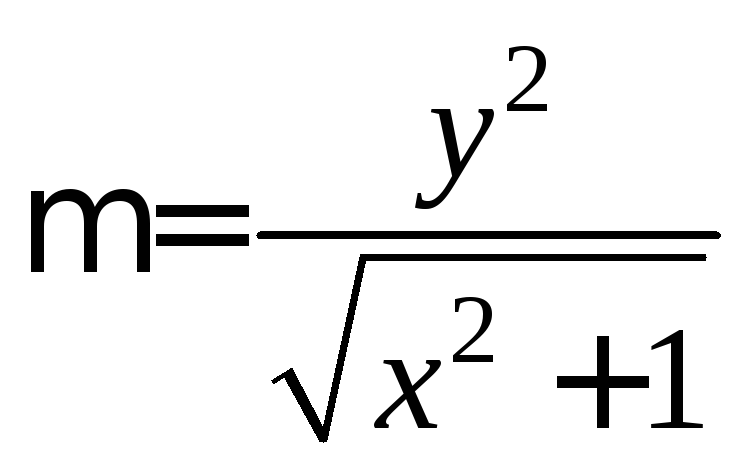 .
.
Решение. В соответствие с формулой (6.13)

