Решение задач

Задача 6.1. Область задается неравенствами:Перейти от двойного интегралак повторному двумя способами.

Решение. Область изображена на рис. 6.8.

Первый способ. Возьмем за внешнюю переменную . Для области. Снизу областьограничена кривой, а сверху – прямой. Тогда в соответствии с формулой (6.1) получаем

.

Второй способ. Теперь возьмем за внешнюю переменную . Поскольку левая часть границы областисостоит из двух участков, заданных разными уравнениями, то нужно разбить областьгоризонтальной прямойна две:и. Для области. Слева областьограничена кривой. Выразим из этого уравнениячерез, учитывая, что. Тогда, используя формулу (6.2), получаем. Для области. Слева и справа областьограничена прямымиисоответственно. Тогда по формуле (6.2) получаем:, откуда

Задача 6.2. Изменить порядок интегрирования в двойном интеграле

.

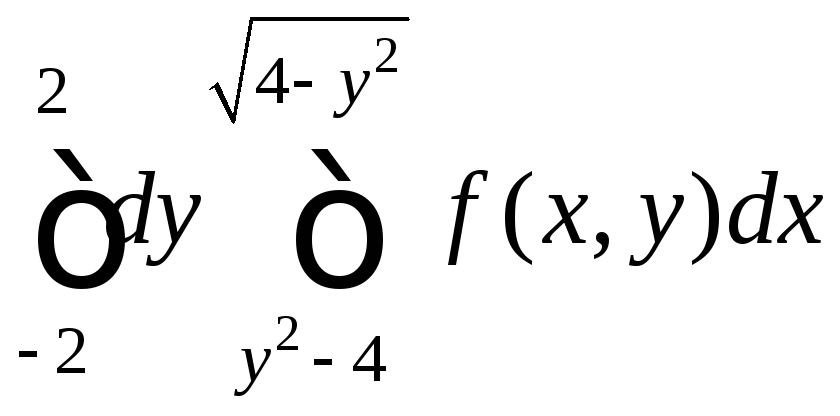Сделать чертеж области .

Решение. Переменная в областиизменяется в промежутке от до , значит, областьзаключена между горизонтальными прямымии. Пределы интегрирования во внутреннем интеграле показывают, что слева областьограничена параболой, а справа – половиной окружности(или). Изобразим область(рис. 6.9).

Теперь поменяем порядок интегрирования, приняв за внешнюю переменную. Разобьем областьна областии.

Для области :,

а для области :

. Тогда

Задача 6.3. Вычислить интеграл , если область D ограничена линиями

Решение. Изобразим область D (рис. 6.10). Координаты точки пересечения кривых находим из системы уравнений

Получаем точку (1;1). Из рисунка видно, что областьD не удовлетворяет условиям теоремы 6.2, но удовлетворяет условиям теоремы 6.3. Поэтому используем формулу (6.2).

Рис. 6.10

Рис. 6.10

Задача 6.4.Вычислить интеграл по областиD, задаваемой неравенствами: Область D изображена на_; рис. 6.11. Она не удовлетворяет как условиям теоремы 6.2, так и условиям теоремы 6.3. Разобьем ее, как показано на рисунке, на области и. Тогда

Вычислим каждый из этих интегралов, беря за внешнюю переменную х, за внутреннюю – у.

Рис. 6.11

Окончательно получаем

Задача 6.5. Вычислить двойной интеграл по области D, определяемой неравенствами

Р

ешение. Для вычисления интеграла перейдем к полярным координатам. Область D (рис. 6.12) представляет собой четверть круга радиусом 2 c центром в начале координат. Она ограничена лучами и (осиОх и Оу соответственно) и кривой (окружность ). Нижний предел изменения это . Тогда, используя формулы (6.6) и (6.7), получаем

Задача 6.6. Вычислить двойной интеграл по области D, задаваемой неравенствами

Решение. Область D (рис. 6.13) – это четверть круга радиусом 1 с центром в точке (1;0). Для вычисления интеграла перейдем к полярным координатам. Запишем уравнения кривых, ограничивающих область D, и определим границы изменения и .

. Таким образом, меняется в пределах от до.

Так как окружность, ограничивающая область D, имеет радиус равный 1, то луч, идущий через точки и ,образует угол с осью. Значит,. Тогда

Задача 6.7. Найти площадь части поверхности параболического цилиндра , лежащей между плоскостями

(при ).

Решение. Заданная часть поверхности изображена на рис. 6.14, а ее проекция на плоскость - на рис. 6.14,б.

Для вычисления площади поверхности воспользуемся формулой (6.10). В нашем примере . Тогда

Задача 6.8. Найти массу плоской пластины, задаваемой неравенствами если ее плотность.

Решение. Данная пластина изображена на рис. 6.15. Она представляет собой часть плоскости, ограниченную дугами окружностей ии прямой. Воспользуемся формулой (6.11) и перейдем к полярным координатам.