Проделаем следующие операции:

1. Разобьем область D сетью кривых на п частей . Обозначим площади этих частей, а диаметры (диаметром области называется максимальное расстояние между всевозможными парами точек области) -. Наибольший из этих диаметров обозначим через.

2. Выберем произвольно в каждой ячейке по точке и вычислим .

3. Составим сумму . Полученная сумма называется интегральной суммой для функции в области D.

4. Вычислим .

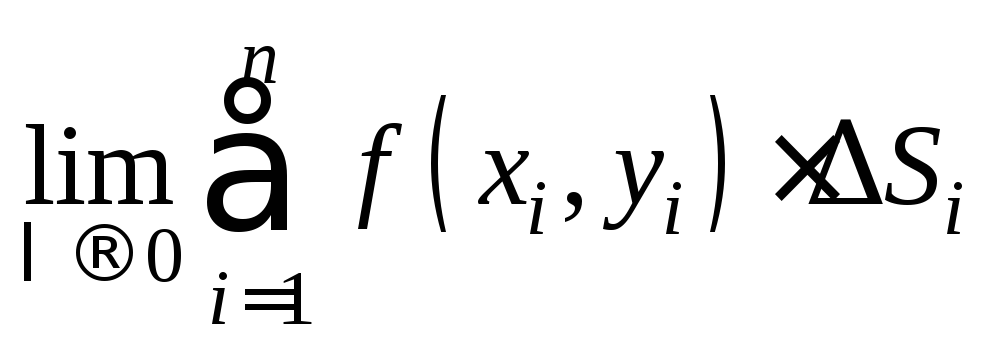Если этот предел существует, конечен и не зависит ни от способа разбиения области D, ни от выбора точек то он называется двойным интегралом от функции по области D и обозначается символами

.

При этом используют следующие названия: - подынтегральная функция, D - область интегрирования, х,у - переменные интегрирования, или dxdy - элемент площади.

Итак, определение двойного интеграла можно записать следующим образом

.

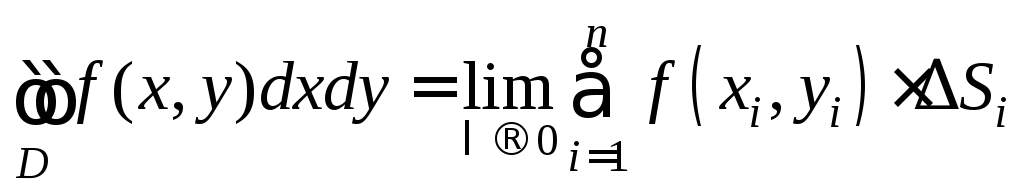Геометрический смысл двойного интеграла

Если в некоторой области D двумерного пространства задана неотрицательная функция , то двойной интеграл представляет собой объем тела, ограниченного снизу областью D, сверху - поверхностью , с боков - цилиндрической поверхностью с образующими, параллельными оси Oz, а направляющей которой является граница области D.

Механический смысл двойного интеграла

Если в некоторой области D двумерного пространства определена неотрицательная функция , задающая плотность фигуры D, то двойной интеграл определяет массу фигуры D.

Теорема 6.1. (Достаточные условия существования двойного интеграла).

Если функция непрерывна в замкнутой и ограниченной области D, ограниченной кусочно-гладкой кривой, то двойной интеграл существует.

Основные свойства двойных интегралов

Здесь мы будем предполагать, что все встречающиеся функции удовлетворяют условиям теоремы существования двойного интеграла. В этом случае справедливы перечисленные ниже свойства.

1. где- площадь области

2. .

3.

Из свойств 2 и 3 следует свойство линейности двойного интеграла:

4. Если всюду в областиD, то .

5. Свойство аддитивности. Если область D разбита на две части и , имеющие лишь общую границу, то

.

6. Есливсюду в областиD, то

.

7. .

8. Теорема о среднем.

Если функция непрерывна в замкнутой ограниченной области D, то в этой области найдется хотя бы одна точка такая, в которой

выполнено равенство

,

где - площадь областиD.

Вычисление двойных интегралов в декартовых координатах

Вычисление двойного интеграла основано на следующей теореме.

Теорема 6.2. (Фубини)^ Если функция непрерывна в замкнутой области D, ограниченной линиями (рис. 6.1), причем функции и непрерывны на промежутке и, то имеет место равенство .

Выражение, стоящее в правой части этого равенства, называется повторным (двукратным) интегралом. Его принято записывать в виде

Тогда можно записать

(6.1)

При использовании формулы (6.1) сначала вычисляется внутренний интеграл при этом считается постоянным. Затем полученная функция, которая зависит уже от переменной , интегрируется пох на промежутке .

Поменяв в предыдущем рассуждении местами переменные х и у, получим следующую теорему.

Теорема 6.3. Если функция непрерывна в замкнутой областиD, ограниченной линиями (рис. 6.2), причем функции и непрерывны на промежутке и , то имеет место равенство

В этом случае сначала вычисляется внутренний интеграл при постоянном .Затем полученная функция переменной у интегрируется по у на промежутке .

Если область D имеет более сложный вид, чем в теоремах 6.2 и 6.3, то следует воспользоваться свойством аддитивности двойного интеграла. А именно, область D нужно разбить на несколько частей, каждая из которых удовлетворяет условиям теоремы 6.2 или 6.3. Интеграл по области D будет равен сумме интегралов по ее частям.

Пример 6.1. Вычислить интеграл если областьD ограничена линиями и осьюОх.

Решение. Изобразим область D (рис. 6.3). Она удовлетворяет условиям теоремы 6.2. Воспользуемся формулой (6.1), т.е. за внешнюю переменную возьмем х, за внутреннюю - у. Внешняя переменная х меняется в пределах от 1 до 2, а внутренняя у - от 0 до 2х (область D снизу ограничена прямой , сверху прямой).

Тогда

Вычисляем внутренний интеграл, считая х постоянным.

Теперь вычисляем внешний интеграл

Замена переменных в двойном интеграле

Преобразование плоских областей

Пусть имеются две плоскости с выбранными на них прямоугольными системами координат Оху и Ouv. Рассмотрим в этих плоскостях две замкнутые области: D – в плоскости Оху и - в плоскостиOuv (рис. 6.4).

Допустим, что имеется система непрерывных функций

(6.3)

которая каждой точке (u,v) области ставит в соответствие одну точку (х,у) области D, причем каждая точка области D соотнесена какой-либо точке области , и разным точкам областисоответствуют разные точки областиD. В таком случае говорят, что формулы (6.3) задают взаимно однозначное отображение области на областьD. Точка (х,у) с координатами и называетсяобразом точки , а, соответственно, точка - прообразом точки (х,у).

Далее мы будем предполагать, что функции (6.3) не только сами непрерывны, но и имеют непрерывные частные производные первого порядка. Введем в рассмотрение определитель

Этот определитель называется определителем Якоби^ или якобианом отображения (6.3). Мы будем предполагать, что в области он отличен от нуля и, значит, в силу непрерывности частных производных сохраняет знак. Можно показать, что при отображении (6.3) линия переходит в линию, область - в область.