4.2. Машина Тьюринга

М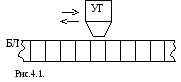одель алгоритма, называемая машиной Тьюринга [16], состоит из бесконечной ленты (БЛ), разделенной на ячейки, и управляющей головки (УГ), которая перемещается по ленте и способна считывать символ в ячейке, против которой она находится, а также замещать обозреваемый символ новым (рис.4.1).

В каждой ячейке может быть записан один символов из ленточного алфавита A. Головка может находиться в одном из внутренних состояний, принадлежащих конечному множеству (алфавиту состояний) Q. Работа машины происходит в дискретном времени в соответствии с программой, задаваемой набором команд вида

qa  a⁺Dq⁺.

В зависимости от состояния головки qQ и символа aA, против которого она стоит, головка записывает на ленте новый символ a⁺ (или оставляет старый), переходит в новое состояние q⁺ (или остается в старом) и передвигается: вправо (П), влево (Л) или остается в прежнем положении (Н).

Назовем конфигурацией машины Тьюринга K_t в момент t содержимое ее ленты, состояние головки qQ и обозреваемый ею символ a. Пусть на ленте записана цепочка символов …a₁a₃a₁a₂a₃a₁…, слева и справа от которой свободные ячейки (содержат символ ), причем головка, находясь в состоянии q_i, обозревает символ a₂. Соответствующую конфигурацию будем записывать, помещая обозначение состояния головки перед обозреваемым символом: a₁a₃a₁q_i a₂a₃a₁.

Конфигурация машины Тьюринга называется заключительной, если головка машины Тьюринга находится в состоянии останова q₀.

Работу машины Тьюринга можно описать как последовательную смену ее конфигураций, причем машина переходит от конфигурации K_t к конфигурации K_t+1 в соответствии со своей программой. Любая начальная конфигурация K₀, которой соответствует состояние q₁, порождает последовательность конфигураций K₀, K₁, K₂, …, K_t,… .

Эта последовательность обрывается, если машина оказывается в заключительной конфигурации. В этом случае будем говорить, что машина Тьюринга применима к конфигурации K₀.

Если последовательность конфигураций K₀, K₁, K₂, …, K_t,… никогда не обрывается, т.е. машина работает вечно (“зацикливается”), будем говорить, что машина Тьюринга неприменима к конфигурации K₀.

Для решения задачи исходные данные должны быть закодированы некоторым “естественным” образом символами некоторого алфавита A и записаны в виде слова X на ленте машины, причем головка в начальном состоянии q₁Q обозревает самый левый символ слова X, т.е. начальная конфигурация имеет вид q₁X. Результирующая конфигурация имеет вид q₀ f(X).

В этом случае будем говорить, что машина Тьюринга вычисляет словарную функцию f(), причем слово f(X) есть значение этой функции для аргумента X. Числовые функции – это частный случай словарных, поскольку конкретный вид символов, которыми оперирует машина, несуществен, также как и тип данных: цифровых, алфавитно-цифровых и т.д.

Примеры машин Тьюринга

Рассмотрим несколько примеров специализированных машин Тьюринга с ленточным алфавитом A={,+,1}, алфавитом состояний {q₀,q₁,q₂, …, q_n} и алфавитом перемещений D{П,Л,Н}. Символ  играет роль разделителя. Символы q₁, q₀ – соответственно начальное и заключительное состояние машины (останов).

Рассматриваемые машины выполняют арифметичекие операции над неотрицательными целыми числами, для представления которых используется унитарнй код. Число x представляется (x+1)-й единицей, причем отдельно записанная единица представляет нулевое значение x.

П

Таблица 4.1

a	q
	q1	q2
	-	1Нq0
1	1Пq2	-

ример 4.1. Прибавление единицы. В таблице 4.1 приведен пример программы машины с алфавитом состояний {q₁,q₂,q₀}. Машина увеличивает значение числа на единицу.

Например, увеличение числа три на единицу машина осуществляет за два шага:

…q₁1111…  …q₂1111…  … q₀11111… .

Для исходной конфигурации …q₁11… поведение машины не определено. Это означает, что рассматриваемая машина реализует частичную словарную функцию.

П

Таблица 4.2

a	q
	q1	q2
	Нq0	1Нq0
1	Пq2	1Нq0

ример 4.2. Усеченное вычитание единицы. В таблице 4.2 приведен пример программы машины, выполняющей усеченное вычитание единицы. Вычитание единицы для неотрицательных целых чисел – частичная функция, поскольку значение 0-1 не определено. Введем усеченное вычитание , доопределив обычное вычитание: xy = x-y для xy и xy =0 для x  y.

Например, усеченное вычитание единицы из четырех машина осуществляет за два шага:

…q₁11111…  …q₂1111…  …q₀1111… .

Усеченное вычитание из нуля:

…q₁1…  …q₂…  …q₀1… .

Пример 4.3. Сложение. В таблице 4.3 приведен пример программы машины с алфавитом состояний {q₁,q₂,q₃,q₀}.

Таблица 4.3

a	q
	q1	q2	q3	q4
	Пq1	Пq1	1Лq2	Нq0
1	Пq3	1Лq2	1Пq3	Пq0
+	Пq4	+Лq2	+Пq3	Нq0

Например, сложение чисел 11+111 (один плюс два) осуществляется за два цикла. Начальное состояние головки q₁. Состояние q₃ поддерживает перемещение головки вправо с одновременным "перетаскиванием" единицы:

…q₁11+111… …q₃1+111… …1q₃+111… …1+q₃111… …1+1q₃11… …1+11q₃1…

…1+111q₃… …1+11q₂11… .

Состояние q₂ соответствует перемещению головки влево:

1+11q₂11… …1+1q₂111… …1+q₂1111… …1q₂+1111… …q₂1+1111… …q₂1+1111…

… q₁1+1111… .

Первый цикл закончен. Второй цикл:

… q₁1+1111… …q₃+1111… …+q₃1111…

. . .

…+ 1111q₃… …+ 111q₂11… …+ 11q₂111…

. . .

…q₂+ 11111… …q₁+ 11111… .

Второй цикл закончен. Машина удаляет лишнюю единицу

…q₁+ 11111… …q₄11111 … …q₀1111…

и, достигнув состояния q₀, останавливается. Конфигурация …q₀11111… дает решение задачи.

Пример 4.4. Усеченное вычитание. В таблице 4.4 приведен пример программы вычисления усеченной разности.

Таблица 4.4

a	q
	q1	q2	q3	q4	q5	q6
	Лq2		Пq4		Пq0	1Нq0
1	1Пq1	Лq3	1Лq3	Пq1	1Лq5	Пq6
	Пq1	1Лq5	Лq3	Пq6		

Например, вычитание 1111111 (три минус два) начинается тремя циклами, в результате каждого из которых стираются крайние единицы содержимого ленты. Начальное состояние q₁ поддерживает перемещение головки вправо до разделителя :

…q₁1111111… . . . …1111111q₁… .

Затем в состоянии q₂ стирается самая правая единица и в состоянии q₃ происходит перемещение головки влево до разделителя :

…1111111q₁… …111111q₂… …11111q₃1…

…1111q₃11… . . . …q₃111111… .

Затем в состоянии q₄ стирается самая левая единица и начинается второй цикл: в состоянии q₁ повторяется перемещение головки вправо до разделителя  и т.д.:

…q₃111111……q₄111111… …q₁11111… … .

Четвертый и последний цикл отличается тем, что, обозревая символ “” в состоянии q₂, головка заменяет его на “1” и переходит в состояние q₅, обеспечивающее корректное завершение программы:

…q₁1… …1q₁… …1q₁… …1q₂…

… q₅11… …q₅11……q₀11… .

Состояние q₆ предусмотрено для случая, когда вычитаемое больше уменьшаемого. В этом состоянии головка очищает ленту: перемещается вправо и стирает все единицы. Встретив разделитель  в состоянии q₆, головка заменяет его единицей, остается на месте и переходит в заключительное состояние q₀.

Приемы программирования машины Тьюринга

Цель настоящего раздела – продемонстрировать универсальные вычислительные возможности машин Тьюринга. Для этого покажем, как можно реализовать на этих машинах основные программные структуры:

• cуперпозицию программ;

• композицию программ;

• ветвление и циклические структуры.

С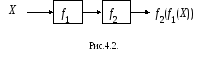уперпозиция программ. Предположим, что машины M₁ и M₂ вычисляют соответственно функции f₁(X) и f₂(X) в одном и том же алфавите A. Построим машину M=M₁M₂ для вычисления суперпозиции f₂(f₁(X)) (рис.4.2). Обозначения состояний машин M₁ и M₂ должны различаться за исключением того, что заключительное состояние M₁ имеет то же обозначение, что и начальное состояние M₂. В таком случае программа машины M получается простым объединением программ M₁ и M₂. Работу машины M=M₁M₂ можно представить схемой

.

Композиция программ. Пусть машины M₁ и M₂ вычисляют функции f₁(X) и f₂(X) соответственно. Построим машину M= M₁*M₂ для вычисления композиции f₁(X)*f₂(X), где * - символ, не встречающийся в алфавитах M₁ и M₂. Машина M использует “двухэтажную” ленту, на которую записываются пары символов вида . СловоX записывается нижними элементами пары вида , где - пустой символ. После запуска M оно переписывается в верхний этаж и оказывается записанным символами вида . ДалееM работает на нижнем этаже как M₁ и вычисляет f₁(X), затем M работает на верхнем этаже как M₂ и вычисляет f₂(X). В завершение M приписывает *f₂(X) в конце записи f₁(X) на нижнем этаже и стирает f₂(X) на верхнем этаже.

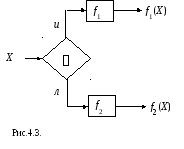
Ветвление программ. Пусть машины M₁ и M₂ вычисляют словарные функции f₁(X) и f₂(X) соответственно в одном и том же алфавите A. Введем символы и (истина) и л (ложь), причем иA и лA. Построим машину M= M₁M₂, которая преобразует слово *X, где {и,л}, в слово f₁(X), если =и, и в слово f₂(X), если =л (рис.4.3). Для этого, полагая что алфавиты состояний M₁ и M₂ различны, в основу M положим объединение их программы. Введем для M начальное состояние q₁ и, полагая, что q_1,1 и q_2,1 – начальные состояния M₁ и M₂ соответственно, дополним объединение программ M₁ и M₂ командами

иq₁  Пq_1,1,

лq₁  Пq_2,1,

*q_1,1  Пq_1,1,

*q_2,1  Пq_2,1.

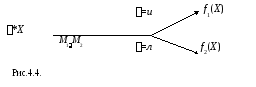
Заключительные состояния q_1,0 и q_2,0 машин M₁ и M₂ обозначим как заключительное состояние q₀ машины M= M₁M₂.

Машину M= M₁M₂ можно представить схемой на рис.4.4.

Ц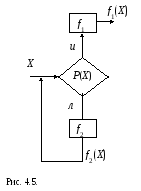иклическая программа. Рассмотрим циклическую программу на рис.4.5. Если значение предиката P(X) истина (и), то программа выдает значение f₁(X). Если же значение предиката P(X) (л), то программа вычисляет значение X⁽¹⁾ =f₂(X) и, если P(X⁽¹⁾)=и, то программа выдает значение f₁(X⁽¹⁾), в противном случае вычисляет значение X⁽²⁾ =f₂(X⁽¹⁾) и т.д.

П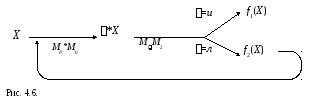риведем схему машины Тьюринга, реализующей циклическую программу (рис.4.6). На этой схеме машинаM_P вычисляет значение  предиката P(X), машина M₀ передает X без изменения, поэтому композиция M_P*M₀ формирует *X. Машины M₁ и M₂ вычисляют f₁(X) и f₂(X) соответственно. Машина M₁M₂ обеспечивает ветвление.