
Механика Лабораторная работа № 11
Министерство образования РФ
Санкт- Петербургский государственный горный институт им. Г.В. Плеханова
(технический университет)
Кафедра общей и технической физики.
Механика
ЛАБОРАТОРНАЯ РАБОТА № 11
Определение отношения теплоёмкости при постоянном давлении к теплоёмкости при постоянном объёме для воздуха методом стоячей волны
САНКТ-ПЕТЕРБУРГ
2003 г.
Цель работы - определить = Cp/CV методом стоячей звуковой волны.
Общие сведения
Р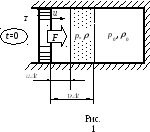 ассмотрим,
как распространяется звуковая волна
в закрытой цилиндрической трубе,
заполненной воздухом. В момент времени
t = 0 мембрана
телефона T (рис.1)
начинает двигаться вправо с постоянной
скоростью
ассмотрим,
как распространяется звуковая волна
в закрытой цилиндрической трубе,
заполненной воздухом. В момент времени
t = 0 мембрана
телефона T (рис.1)
начинает двигаться вправо с постоянной
скоростью
![]() .
Молекулы воздуха вблизи мембраны придут
в движение и тоже будут перемещаться
вправо со скоростью
.
Молекулы воздуха вблизи мембраны придут
в движение и тоже будут перемещаться
вправо со скоростью
![]() .
Непосредственно около мембраны
возникнет область сжатия, давление
внутри которой р = р0 + р,
где р0 - первоначальное давление
воздуха. Сжатый слой воздуха передаст
импульс молекулам, расположенным справа,
приводя таким образом в движение
соседний слой. В течение второй части
периода мембрана движется влево, создавая
справа от себя область разрежения, в
которую устремляются молекулы из сжатого
слоя. Таким образом, молекулы воздуха
совершают колебательное движение в
направлении колебаний мембраны. В среде
при этом распространяются, чередуясь,
области сжатия и разрежения воздуха
(области повышенного и пониженного
давления), что и представляет собой
бегущую звуковую волну. Звук является
продольной волной, т.к. частицы среды
совершают колебания вдоль направления
распространения. Будем описывать
распространение волны с помощью фазовой
скорости
.
Непосредственно около мембраны
возникнет область сжатия, давление
внутри которой р = р0 + р,
где р0 - первоначальное давление
воздуха. Сжатый слой воздуха передаст
импульс молекулам, расположенным справа,
приводя таким образом в движение
соседний слой. В течение второй части
периода мембрана движется влево, создавая
справа от себя область разрежения, в
которую устремляются молекулы из сжатого
слоя. Таким образом, молекулы воздуха
совершают колебательное движение в
направлении колебаний мембраны. В среде
при этом распространяются, чередуясь,
области сжатия и разрежения воздуха
(области повышенного и пониженного
давления), что и представляет собой
бегущую звуковую волну. Звук является
продольной волной, т.к. частицы среды
совершают колебания вдоль направления
распространения. Будем описывать
распространение волны с помощью фазовой
скорости
![]() -
скорости распространения в пространстве
поверхностей, образованных частицами,
совершающими колебания в одинаковой
фазе.
-
скорости распространения в пространстве
поверхностей, образованных частицами,
совершающими колебания в одинаковой
фазе.
Импульс силы
![]() ,
с которой мембрана в течение времени
t
давит на газ
,
с которой мембрана в течение времени
t
давит на газ
![]() ,
(1)
,
(1)
где
S
- площадь мембраны, p
– избыточное давление, обусловленное
силой
![]() .
.
С другой стороны, импульс внешней силы равен приращению импульса (количества движения), которое получил газ:
![]() ,
(2)
,
(2)
где
![]() - плотность сжатого воздуха;
- плотность сжатого воздуха;
![]() - плотность воздуха в начальный момент
времени;
- плотность воздуха в начальный момент
времени;
![]() - масса сжатого воздуха;
- масса сжатого воздуха;
![]() - длина столба воздуха (путь, который
прошла волна за время
- длина столба воздуха (путь, который
прошла волна за время
![]() ).
Объединяя равенства (1) и (2), получим
).
Объединяя равенства (1) и (2), получим
![]() .
(3)
.
(3)
До движения мембраны
масса воздуха m в
отрезке трубы длиной
![]() составляла 0
составляла 0![]() .
При смещении мембраны на ut
плотность воздуха меняется, и в этом
случае его массу можно представить
(рис. 1)
.
При смещении мембраны на ut
плотность воздуха меняется, и в этом
случае его массу можно представить
(рис. 1)
![]() ,
,
или
![]() ,
,
После простых алгебраических преобразований получим
![]() .
(4)
.
(4)
Подставив равенство (3) в формулу (4), можно записать
![]() .
(5)
.
(5)
Если изменения плотности и давления малы ( << 0 и p << p0), то скорость распространения волны
![]() .
(6)
.
(6)
С точки зрения термодинамики процесс распространения звуковой волны в газе можно рассматривать как адиабатический, так как изменение давления происходит так быстро, что смежные области среды не успевают обмениваться теплом.
Адиабатический процесс описывается уравнением pV = const. Так как V = M/ (здесь М - масса газа), то p(M/) = const. Продифференцировав это равенство с учётом изменения давления и плотности, получим
![]() ,
,
откуда
![]() ,
,
т.е. в соответствии с формулой (6)
![]() ,
(7)
,
(7)
где - плотность газа при данном давлении и температуре, = p/RT; - молярная масса газа; R - универсальная газовая постоянная; T - абсолютная температура.
Подставив в уравнение (7), получим
![]() ,
,
откуда
![]() .
(8)
.
(8)
Таким образом, для вычисления необходимо определить скорость распространения звуковых колебаний. В работе эта скорость определяется методом стоячей волны.
Если в трубе, один конец которой закрыт, возбудить звуковые колебания, в ней в результате наложения двух встречных волн (прямой и отражённой) с одинаковыми частотами и амплитудами будут возникать стоячие волны. В определенных точках амплитуда стоячей волны равна сумме амплитуд обоих колебаний и имеет максимальное значение; такие точки называются пучностями. В других точках результирующая амплитуда равна нулю, такие точки называются узлами. Расстояние между ближайшим узлом и пучностью равно /4, где - длина бегущей звуковой волны. Таким образом, измерив расстояние между узлом и пучностью или между двумя ближайшими пучностями (/2), можно найти длину бегущей звуковой волны . Фазовая скорость волны рассчитывается через длину волны по соотношению
= , (9)
где - частота колебаний.
