
Апроксимация функции в MathCAD
.pdfАппроксимация функций с помощью MathCAD
КПРАКТИЧЕСКОЙ ЧАСТИ
1.Линейная регрессия
Линейная регрессия в системе Mathcad выполняется по векторам аргумента Х и от-
счетов Y функциями:
intercept(X,Y) – вычисляет параметр а1, смещение линии регрессии по
вертикали;
slope(X,Y) – вычисляет параметр a2, угловой коэффициент линии регрессии.
Полученные значения коэффициентов используем в уравнении регрессии y(x) = a1+a2*x.
Функция corr(Y,y(x)) вычисляет коэффициент корреляции Пирсона. Чем он ближе к 1, тем точнее обрабатываемые данные соответствуют линейной зависимости.
2. Полиномиальная регрессия
Одномерная полиномиальная регрессия с произвольной степенью n полинома с произвольными координатами отсчетов в Mathcad выполняется функциями:
regress(X,Y,n) – вычисляет вектор S, в составе которого находятся коэффици-
енты ai полинома n-й степени;
Значения коэффициентов ai могут быть извлечены из вектора S функцией submatrix(S, 3, length(S)-1, 0, 0).
Полученные значения коэффициентов используем в уравнении регрессии y(x) = a1+a2*x+a3*x2.
3. Нелинейная регрессия
Для простых типовых формул аппроксимации предусмотрен ряд функций нелиней-
ной регрессии, в которых параметры функций подбираются программой Mathcad.
К их числу относится функция expfit(X,Y,S), которая возвращает вектор, со-
держащий коэффициенты a1, a2 и a3 экспоненциальной функции y(x) = a1·exp(a2·x) + a3.
В вектор S вводятся начальные значения коэффициентов a1, a2 и a3 первого приближения.
Пример расчетов в среде MathCAD
Исходные данные:
|
|
|
|
|
0 |
16 |
|
|
|
|
|
|
|
|
|
|
|
0.4 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0.7 |
25.5 |
|
|
|
|
|
||
|
|
|
|
|
1 |
34 |
|
|
|
|
|
|
|
|
|
|
|
1.5 |
40.7 |
|
|
|
|
|
|
|
|
m |
|
|
|
|||||||
|
|
|
49 |
x m |
0 |
y m |
1 |
|||||
|
|
|
|
1.9 |
|
|
|
|
|
|
||
|
|
|
|
|
2.5 |
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2.9 |
69.6 |
|
|
|
|
|
||
|
|
|
|
3.6 |
89 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.3 |
98.3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
0 |
0 |
|
|
|
|
|
|
|
0 |
16 |
|
|
1 |
0.4 |
|
|
|
|
|
|
|
1 |
20 |
|
|
2 |
0.7 |
|
|
|
|
|
|
|
2 |
25.5 |
|
x |
3 |
1 |
|
|
|
|
|
|
y |
3 |
34 |
|
4 |
1.5 |
|
|
|
|
|
|
4 |
40.7 |
|||
|
5 |
1.9 |
|
|
|
|
|
|
|
5 |
49 |
|
|
6 |
2.5 |
|
|
|
|
|
|
|
6 |
60 |
|
|
7 |
2.9 |
|
|
|
|
|
|
|
7 |
69.6 |
|
|
8 |
3.6 |
|
|
|
|
|
|
|
8 |
89 |
|
|
9 |
4.3 |
|
|
|
|
|
|
|
9 |
98.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
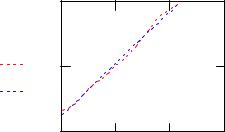
Линейная регрессия:
a1 |
intercept(x y) |
|
a1 |
12.665 |
|
a2 |
slope(x y) |
|
a2 |
19.971 |
|
f(x) a1 |
a2 x |
corr(y f(x)) 0.997 |
100
y
f(x) 50
0
0 |
2 |
4 |
6 |
x
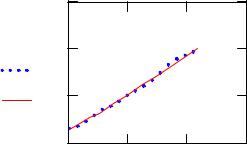
Полиномиальная регрессия (n=2): |
||||
s regress(x y 2) |
|
|
|
|
coeff submatrix(s 3 length(s) |
1 0 0) |
|||
A coeff |
|
|
|
|
a1 A0 |
|
a1 14.494 |
|
|
a2 A1 |
|
a2 16.96 |
|
|
a3 A2 |
|
a3 0.714 |
|
|
f(x) a1 |
a2 x a3 x2 |
corr(y f(x)) 0.998 |
||
|
150 |
|
|
|
y |
100 |
|
|
|
|
|
|
|
|
f(x) |
50 |
|
|
|
|
|
|
|
|
|
0 |
2 |
4 |
6 |
|
0 |
|||
|
|
x |
|
|
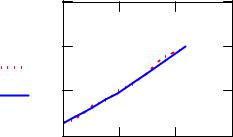
Экспоненциальная регрессия (n=2): |
||||||
1 |
|
|
|
|
|
|
s 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
169.694 |
||
A expfit(x y s) |
A |
|
0.095 |
|
||
|
|
|
|
|
|
|
|
|
|
|
154.614 |
||
a1 A0 |
|
a1 169.694 |
|
|
|
|
a2 A1 |
|
a2 0.095 |
|
|
|
|
a3 A2 |
|
a3 154.614 |
|
|
|
|
f(x) a1 ea2 x a3 |
corr(y f(x)) 0.997 |
|||||
|
|
150 |
|
|
|
|
|
y |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
f(x) |
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
0 |
2 |
|
4 |
6 |
|
|
0 |
|
|||
|
|
|
|
x |
|
|
Вывод: сравнивая результаты вычислений, можно сделать вывод, что самый высокий коэффициент детерминированности (корреляции) – в случае полиноми-
альной регрессии второй степени (0.998).
Следовательно, что квадратичная аппроксимация наилучшим образом описы-
вает экспериментальные данные.
