
- •ГЛАВА 2. НЕЛИНЕЙНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА
- •ГЛАВА 3. НЕЛИНЕЙНЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- •ГЛАВА 8. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ЦЕПЯХ
- •Введение
- •ГЛАВА 11. Моделирование процессов в электрических цепях
- •Правильные ответы на вопросы тестов к главам 1 –9
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •Предметный указатель
в. Отношение спектральной характеристики входного напряжения U1(j ) к спектральной характеристике выходного напряжения U2(j ).
ГЛАВА 8. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ЦЕПЯХ
8.1.Общая характеристика переходных процессов
внелинейных цепях
Методы анализа и расчета переходных процессов в нелинейных цепях могут быть классифицированы: а) по виду основных операций, которые необходимо выполнять для интегрирования нелинейных дифференциальных уравнений — на графические (графоаналитические) и аналитические; б) по характеру величины, для которой производится расчет (по мгновенным значениям токов и напряжений), по мгновенным значениям огибающих токов и напряжений (их первых гармоник) либо по мгновенным значениям медленно меняющихся средних за период внешнего воздействия значений.
Под графическими (графоаналитическими) понимают такие методы, в которых основными операциями при определении зависимости от времени искомых токов и напряжений являются графические построения, нередко сопровождаемые и некоторыми вспомогательными числовыми подсчетами. В графических методах характеристики нелинейных элементов обычно не требуется выражать аналитически.
Аналитическими называют такие методы, в которых основной операцией при определении зависимости искомых токов и напряжений от времени является точное (приближенное) аналитическое интегрирование дифференциальных уравнений цени путем использования аналитических выражений характеристик нелинейных элементов.
Ниже рассмотрены следующие аналитические методы: 1) метод интегрируемой нелинейной аппроксимации; 2) метод кусочно-линейной аппроксимации; 3) метод медленно меняющихся амплитуд; 4) метод малого параметра.
Графические методы имеют следующие преимущества перед аналитическими:
а) нет необходимости выражать характеристики нелинейных элементов аналитически, что позволяет избавиться от погрешностей, связанных с аналитическим представлением характеристик;
б) простота учета гистерезиса и других сложных нелинейных зависимо-
стей.
В свою очередь, аналитические методы также имеют перед графическими преимущества. Из них основным является то, что они дают возможность получить решение в общем виде, а не для какого-то одного конкретного сочетания параметров. Получить решение в общем виде желательно потому, что анализ его позволяет выяснить все особенности процесса при изменении всех параметров.
Как упоминалось, все методы расчета могут быть подразделены на две подгруппы: 1) расчет по мгновенным значениям токов и напряжений; 2) расчет по мгновенным значениям огибающих токов и напряжений.
Расчет по огибающим важен, потому что он дает возможность, не вдаваясь в мелкие детали процесса внутри каждого периода действующей в схеме периодической ЭДС (внутри каждого периода автоколебаний в автоколебательной системе), судить о макроструктуре процесса. Он возможен не только для нелинейных цепей, он представляет существенный интерес и для линейных цепей.
Точность расчета по огибающим уступает точности расчета по мгновенным значениям. Однако возможность судить о макроструктуре процесса часто является решающим фактором.
Там, где это необходимо, целесообразно дополнять расчет по огибающим расчетам по мгновенным значениям. Метод расчета по огибающим представлен методом медленно меняющихся амплитуд. Остальные методы относятся к подгруппе расчета по мгновенным значениям.
Вцепях с сосредоточенными параметрами энергия электрического поля
вемкостях, по существу, определяется их зарядами q , энергия магнитного поля
виндуктивностях — их потокосцеплениями . В линейных цепях эти величины пропорциональны соответственно напряжению uC q / C и току iL Ψ/ L ,
откуда из невозможности скачков энергии, т. е. ее мгновенного изменения на конечную величину, вытекает невозможность скачкообразного изменения как q и , так и uC , и iL . Последнее и использовалось в гл. 5 для определения начальных условий при расчете переходных процессов.
В нелинейных цепях зависимости q uC и Ψ iL нелинейны; возможны, например, при гистерезисе нулевые значения uC и iL при ненулевых значениях q и , и наоборот. Поэтому для определения начальных условий на основе невозможности скачкообразного изменения энергии правильней исходить из не-
возможности скачков q и . Затем, определив зависимости q t и t и используя кривые q uC и Ψ iL можно найти зависимости uC t и iL t .
Переходные процессы в нелинейных цепях описываются нелинейными дифференциальными уравнениями. Эти уравнения не имеют общего метода решения.
Для решения этих уравнений применяются приближенные аналитические, графоаналитические и графические методы. Далее на примерах, имеющих практическое значение, показывается применение следующих основных методов, частично использованных ранее при анализе установившихся режимов в нелинейных цепях:
1.Деление процесса на последовательные интервалы времени, внутри которых нелинейное уравнение заменяется линейным уравнением с постоянными коэффициентами.
2.Линеаризация второстепенных членов уравнения, превращающая уравнение в линейное, с возможностью применения последовательных приближений.
3.Кусочно-линейная аппроксимация нелинейной характеристики ломаной прямой, для прямолинейных участков которой составляются и решаются линейные уравнения с последующим припасовыванием предыдущих и последующих участков.
4.Аналитическая аппроксимация нелинейной характеристики, позволяющая получить аналитическое решение дифференциального уравнения переходного процесса.
5.Графическое интегрирование кривой, построенной таким образом, чтобы ограниченная ею плошдль была пропорциональна времени, соответствующему каждому значению исследуемой функции; этот метод применим для уравнений первого порядка, допускающих разделение переменных.
8.2. Решение, основанное на графическом подсчёте определенного интеграла
Метод применим к нелинейным электрическим цепям, описываемым дифференциальными уравнениями первого порядка, допускающими разделение переменных. Последняя оговорка свидетельствует о том, что метод применим к цепям постоянного тока и, как правило, неприменим к цепям переменного тока. Основные этапы и последовательность расчета проиллюстрируем на примере.

Пример. Нелинейный конденсатор через резистор подключается к источнику напряжения U (рис. 8.1, а). Кулонвольтная характеристика конденсатора задана графически (рис. 8.1, б). Полагая, что в схеме присутствуют нулевые начальные условия, необходимо построить кривые изменения заряда q, напряжения на конденсаторе uC и тока i в функции времени. Составим дифференци-
альное уравнение:
uC q R |
d q |
U . |
(8.1) |
|
d t |
||||
|
|
|
а) б)
Рис. 8.1. Подключение резистора через нелинейный конденсатор
Разделим переменные: |
|
|
|
|
|
|
|
|
d t R |
d q |
|
|
|
или d t R F q d q , |
(8.2) |
||
U uC q |
||||||||
|
|
|
|
|||||
где |
|
|
|
|
|
|
|
|
|
F q |
|
|
|
1 |
. |
(8.3) |
|
|
U uC q |
|||||||
Для построения кривой F q (pис. 8.2,б) используем кулонвольтную характеристику. Левую часть уравнения (8.2) проинтегрируем по t от 0 до текущего значения t , а правую по q — от q = 0 до текущего значения q . В результате получим
q |
|
t R F q d q . |
(8.4) |
0 |
|
Графически подынтегральное выражение F q d q |
представляет собой |
заштрихованную площадку (рис. 8.2, б). |
|

Кривая 1 на рис. 8.2, а качественно представляет собой зависимость q от t . С помощью кривой q f t и кулонвольтной характеристики нелинейного
конденсатора строят зависимость uC t (кривая 2).
Ток в цепи для произвольного момента времени определяется по формуле i U uC / R (кривая 3).
1
а) б)
Рис. 8.2. Расчётные характеристики для цепи, изображенной на рис. 8.1
8.3. Решение методом кусочно-линейной аппроксимации
При расчете этим методом осуществляется замена характеристики нелинейного элемента отрезками прямых линий, что позволяет перейти от нелинейного дифференциального уравнения к нескольким линейным уравнениям, отличающимся друг от друга лишь значениями коэффициента.
Каждое из линейных уравнений справедливо для того интервала времени, в течение которого рабочая точка перемещается по соответствующему линеаризованному участку. Метод применим к цепям, содержащим источники постоянной и (или) синусоидальной ЭДС, а также к цепям первого и более высоких порядков.
Для сложных нелинейных цепей с источником (источниками) синусоидальной ЭДС основная трудность расчета данным методом заключается в определении постоянных интегрирования, исходя из законов коммутации и времени работы на каждом линейном участке. В сложных цепях неизвестные находят обычно из трансцендентных уравнений, часто применяют ЭВМ. Впервые идея этого метода была высказана русским физиком Н. Д. Папалекси в 1912 г.
Рассмотрим основные этапы расчета на примере.
Пример. Конденсатор емкостью С заряжается через нелинейный резистор (HP) от источника постоянного напряжения U (рис. 8.3, а). Определить закон изменения тока в цепи при зарядке.

Решение. Вольт-амперную характеристику HP заменим двумя отрезками прямых линий (рис. 8.3, б). Пусть на участке от i 0 до i i1 , uHP k2 i , где
uHP |
- напряжение на нелинейном резисторе; k2 - коэффициент. На участке |
i i1 , |
uHP U0 k1 i . |
Рис. 8.3. Зарядка конденсатора через нелинейный резистор (НР) Размерности коэффициентов k1 и k2 соответствуют размерности сопро-
тивления. В уравнение цепи uC uHP U вместо uC подставим (1/ C) i d t , заменим uHP для первого участка на U0 k1i , а для второго – на k2 i .
При зарядке конденсатора ток постепенно уменьшается от максимального значения до нуля. Поэтому изображающая точка перемещается сначала по первому участку, а затем по второму.
Для первого участка |
— |
|
(1/ C) i d t U0 |
k1 i U ; для второго — |
||||
(1/ C) i d t k2 i U . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
Для первого участка i i |
i |
|
|
|
|
|||
|
|
|
||||||
|
|
0 A1 exp |
k C . |
|||||
|
|
|
|
|
|
|
1 |
|
Постоянную интегрирования |
|
A1 |
|
найдем |
из начального условия: |
|||
t 0, uC 0 . Поэтому U0 k1 i 0 U |
и i 0 A1 |
U U0 / k1. Следователь- |
||||||
но, при работе на первом участке |
|
|
|
|
|
|
|
|
|
U U0 |
|
|
|
t |
|
|
|
i |
|
|
|
|
|
|
||
k |
exp |
|
|
. |
(8.5) |
|||
k |
C |
|||||||
|
1 |
|
|
1 |
|
|
|
|
Пусть при t t1 ток i i1 . Подставим в (8.5) решим полученное уравнение относительно t1 :
t1 k1 C lnU k iU0 .
1 1
i1 вместо i и t1 вместо t и
(8.6)

|
|
t t1 |
|
|
|
|
|
|
, причем |
A2 i1 . |
|
При работе на втором участке i A2 exp |
k2 C |
|
|||
|
|
|
|
|
8.4. Решение методом интегрируемой нелинейной аппроксимации
Метод основан на аппроксимации характеристики нелинейного элемента такой нелинейной функцией, которая, во-первых, достаточно точно отображает его характеристику в предполагаемом интервале перемещения изображающей точки по ней и, во-вторых (и это главное), дает возможность точно проинтегрировать уравнение в известных функциях.
Ценность метода заключается в том, что в результате интегрирования получают зависимость исследуемой величины от времени и всех параметров схемы.
Метод применим к дифференциальным уравнениям первого порядка, а также к уравнениям, сводящимся к уравнениям первого порядка путем замены переменных.
Пример. Определить закон нарастания во времени тока при замыкании ключа в схеме (рис. 8.4). Зависимость тока от потокосцепления выражена
формулой i k Ψ4 . В схеме нулевые начальные условия.
|
|
Рис. 8.4. Схема с нелинейной индуктивностью |
|
|
||||||
Решение. Из уравнения цепи d R i U |
следует, что d t |
d |
. |
|||||||
U R i |
||||||||||
|
|
d t |
|
|
|
|
||||
Вынесем из знаменателя множитель R и заменим i на k Ψ4 : |
|
|
||||||||
|
|
d t |
1 |
|
d Ψ |
|
, |
|
|
|
|
|
|
I y k Ψ4 |
|
|
|||||
|
|
|
R |
|
|
|
||||
где I y U / R . |
|
|
|
|
|
|
|
|
|
|
Обозначим I |
y |
a2 и заменим k Ψ4 |
на Ψ4 ; d на d Ψ / 4 k . В результате |
|||||||
|
|
|
|
1 |
|
1 |
|
|
||
получим

d t |
1 |
|
d Ψ |
; |
1 |
|
1 |
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
; |
|||||
|
R4 k |
|
a2 Ψ4 |
|
a2 Ψ4 |
|
2a |
|
a Ψ2 |
|
a Ψ2 |
|
|
|
|
1 |
|
1 |
|
|
|
1 |
|
1 |
|
|
1 |
|
1 4 |
i / I y |
|
|
|
t |
|
0,5ln |
|
|
|
arctg4 i / I y . |
(8.7) |
2 I 0,75 R k 0,25 |
1 4 |
i / I |
|
||||
|
|
y |
|
|
|||
|
y |
|
|
|
|
|
|
С помощью (8.7) можно определить время, которое необходимо, чтобы отношение i / I y достигло заданного значения.
8.5.Решение методом медленно меняющихся амплитуд
Вэлектро- и радиотехнике для расчетов переходных процессов широко применяют метод медленно меняющихся амплитуд. Этот метод был предложен
в1921 г. голландским ученым Ван-дер-Полем.
Рассмотрим основы этого метода на примере нелинейной цепи второго порядка, находящейся под воздействием периодической возмущающей силы.
Пусть уравнение этой цепи записано следующим образом:
d 2 x |
f x d x |
02 x Asin t . |
(8.8) |
d t 2 |
d t |
|
|
Под действием периодической силы с частотой в цени устанавливается вынужденное колебание, первая гармоника которого имеет частоту . Полага-
ем, что высшие гармоники выражены слабо. |
|
Искомая функция x(t) может быть представлена как |
|
x a sin t b cos t , |
(8.9) |
где а и b — медленно меняющиеся во времени амплитуды искомого колебания. Медленность изменения а и b во времени определяется тем, что их производные по времени являются величинами первого порядка малости по срав-
нению с произведениями a и b :
|
|
|
d a |
a ; |
d b |
b . |
|
|
|
(8.10) |
|
|
|
|
|
|
|
|
|
||||
|
|
|
d t |
d t |
|
|
|
|
|||
Если это учесть, то, вместо того, чтобы взять |
|
|
|
|
|||||||
|
d x |
a cos t b sin t sin t |
d a |
cos t |
d b |
, |
(8.11) |
||||
|
d t |
d t |
d t |
||||||||
|
|
|
|
|
|
|
|
|
|||
можно в первом приближении принять
d x |
a cos t b sin t . |
(8.12) |
|
d t |
|||
|
|
Аналогично вместо того, чтобы вторую производную брать в виде
|
|
|
d 2 x |
a 2 sin t b 2 cos t cos t d a |
sin t d b |
|
|||||||||||||||||
|
|
|
d t 2 |
|
|
|
|
|
|
|
|
|
|
d t |
|
|
|
d t |
|
||||
|
|
|
|
|
d 2a |
sin t |
d 2b |
cos t cos t |
d a |
sin t |
d b |
, |
|
||||||||||
|
|
|
|
d t 2 |
d t2 |
d t |
d t |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
пренебрежем |
|
в ней |
слагаемыми |
второго |
порядка |
малости |
|
(учтем, что |
|||||||||||||||
d 2a |
|
d a |
и |
d 2b |
|
d b |
) и составим слагаемые первого порядка малости. В |
||||||||||||||||
d t2 |
d t |
d t |
2 |
d t |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
результате получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
d |
2 |
|
|
2a 2 d b |
|
|
|
|
|
|
|
|
|
(8.13) |
|||||
|
|
|
|
|
x |
sin t 2b 2 d a |
cos t . |
||||||||||||||||
|
|
|
|
d t |
2 |
|
|
|
d t |
|
|
|
|
d t |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Обратим внимание на то, что слагаемые первого порядка малости оставлены в выражении для d 2 x / d t2 и их не учитывают в выражении для d x / d t .
Объясняется это тем, что исследуемая цепь обладает малыми потерями, поэтому амплитуда второго слагаемого левой части (8.8) относительно мала по сравнению с амплитудами первого и третьего слагаемых левой части (8.8).
В функцию f(x) вместо х подставим (8.9) и разложим f(x) в ряд Фурье. Затем умножим ряд Фурье, которым выразилось f(x) на d x / d t [нa правую часть (8.12)]. Таким образом,
f x |
d x |
F a,b |
F a,b sin t F a,b cos t F a,b sin 2 t |
|
|||
|
|
||||||
|
|
d t |
0 |
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
F4 a,b cos 2 t .... |
|
|
(8.14) |
||||
|
|
Так как расчет ведется по первой гармонике, то постоянной |
|
||||
составляющей F0 a,b и высшими гармониками ряда Фурье [ F3 a,b , |
F4 a,b и |
||||||
др.] в дальнейшем пренебрегаем. |
|
|
|||||
|
|
В (8.8) |
подставим |
правую часть |
(8.13) вместо |
d 2 x / d t2 , |
|
F |
a,b sin t F a,b cos t |
вместо f x d x / d t |
и 2 a sin t b cos t вместо |
||||
1 |
|
|
2 |
|
|
0 |
|
02 x . |
|
|
|
|
|
||
Тогда (8.8) можно разбить на два уравнения. Одно из них [уравнение (8.8)] будет выражать собой равенство коэффициентов при cos t в левой и правой частях (8.8), другое [уравнение (8.16)] — равенство коэффициентов при sin t в левой и правой частях (8.8):

2 |
d b |
F |
a,b a 2 |
2 A; |
(8.15) |
||
|
|
||||||
|
|
d t |
1 |
0 |
|
|
|
|
|
|
|
|
|
||
2 |
d a |
F |
a,b b 2 |
2 0 . |
(8.16) |
||
|
|||||||
|
d t |
2 |
0 |
|
|
||
|
|
|
|
|
|||
Система уравнений (8.15) и (8.16) представляет собой два совместных дифференциальных уравнения, составленных относительно мгновенных значений медленно меняющихся амплитуд a и b .
В общем случае решение этой системы может производиться методом малого параметра или методами численного интегрирования. В частном случае, когда внешняя периодическая сила равна нулю ( A 0 ) и функция F1 a,b 0, система сводится к одному дифференциальному уравнению первого порядка:
d a |
|
F2 a |
b 0 . |
(8.17) |
d t |
|
|||
|
2 |
|
||
Ранее были рассмотрены основные этапы перехода от дифференциального уравнения для мгновенных значений [уравнение (8.8)] к дифференциальным уравнениям для медленно меняющихся амплитуд. Метод применим и к уравнениям более высоких порядков.
В заключение необходимо отметить, что если максимальное значение слагаемого f x d x / d t в (8.8) (и подобных ему), выражающее собой падение напряжения в активном сопротивлении контура (контуров), соизмеримо с максимальными значениями остальных слагаемых (8.8), то в выражении d x / d t
должны быть сохранены слагаемые первого порядка малости, которыми ранее пренебрегли. Огибающая колебаний определяется уравнением
f t |
a2 t b2 t . |
(8.18) |
8.6. Переходные процессы в цепях с ферромагнитными катушками
Методы расчета переходных процессов в ферромагнитных катушках.
Ферромагнитные катушки представляют собой пример индуктивных нелинейных элементов цепи переменного тока, поскольку их индуктивность L меняется в зависимости от тока цепи. В результате дифференциальные уравнения, описывающие переходные процессы в цепях с такими катушками, становятся нелинейными, и на пути их интегрирования в общем случае возникают серьезные трудности.
Практически при решении нелинейных дифференциальных уравнений приходится или прибегать к графическим приемам интегрирования или, пред-
почитая аналитический метод, идти на определенные допущения, позволяющие свести нелинейную задачу к приближенному линейному варианту.
Ниже приводятся два примера анализа переходных процессов в цепях с ферромагнитными катушками, в первом из которых иллюстрируется графический метод интегрирования уравнения, а во втором — приближенное аналитическое решение задачи.
Включение ферромагнитной катушки под постоянное напряжение.
Пусть ферромагнитная катушка L с сопротивлением обмотки R в момент времени t = 0 присоединяется к источнику с постоянным напряжением U (рис. 8.5, а). Уравнение, записанное для замкнутой цепи по второму закону Кирхгофа,
будет иметь вид |
|
|
|||||
Ri U eL . |
(8.19) |
||||||
Выразив ЭДС самоиндукции катушки через ее потокосцепление: |
|
||||||
eL |
d Ψ |
, |
|
(8.20) |
|||
|
|
|
|||||
|
d t |
|
|
||||
получим дифференциальное уравнение |
|
|
|||||
U Ri |
d |
|
, |
(8.21) |
|||
d t |
|||||||
|
|
|
|
||||
в котором потокосцепление катушки связано с током i нелинейной магнитной характеристикой катушки, заданной в виде графика, приведенного на рис. 8.5, б.
По этой характеристике, в частности, можно определить установившееся значение потокосцепления (операция а – б), если предварительно вычислить установившийся ток цепи по очевидной формуле:
i UR . |
(8.22) |
Однако эта нелинейная связь не позволяет решить полученное дифференциальное уравнение аналитически, и его интегрирование придется выполнить графическим путем. Для этого, осуществляя разделение переменных, представим уравнение в виде
d t |
d |
(8.23) |
|
U Ri |
|||
|
|
и обратимся к его интегрированию в пределах некоторого интервала времени t, начиная от момента замыкания цепи (t = 0),

t |
Ψ |
d Ψ |
|
|
|
d t |
|
. |
(8.24) |
||
U Ri |
|||||
0 |
0 |
|
|
||
|
|
|
|||
При этом пределы интегрирования в правой части равенства выбраны в соответствии с изменением потокосцепления за тот же интервал времени – от нуля (остаточным пото-косцеплением пренебрегаем) до некоторого значения
.
Интегрирование левой части равенства не представляет никаких затруднений (в результате мы получим упомянутое выше время t), а в правой части эту операцию выполним графическим путем, предварительно построив подынтегральную функцию
f |
1 |
. |
(8.25) |
|
U Ri |
||||
|
|
|
||
Для этого, задаваясь рядом произвольных значений 1, 2 ,..., i ,... |
пото- |
|||
косцепления, вплоть до его установившегося значения , определим для каждого из них, пользуясь магнитной характеристикой катушки (рис. 8.5, б), соответствующие значения i1,i2 ,...,ii... тока i (операция в–г). В свою очередь, для каждого полученного тока по приведенному выражению рассчитаем значение подынтегральной функции f и построим ее (рис. 8.5, в), откладывая по оси абсцисс выбранные значения потокосцепления, а по оси ординат соответствующие значения функции f . Очевидно, что при 0 , чему соответствует
i 0 , подынтегральная функция приобретает значение 1/U , а при установившемся значении потокосцепления , которое отвечает установившемуся току катушки i U / R , функция f обращается в бесконечность.
Определенный интеграл этой функции
Ψ d Ψ
0 U Ri ,
взятый в пределах от 0 до некоторого значения потокосцепления , как известно, представляет собой величину, пропорциональную площади s , ограниченной интегрируемой функцией, осью абсцисс и вертикальными прямыми, которые определяют диапазон интегрирования (на рис. 8.5, в эта площадь заштрихована). И так как этот интервал равен времени t, которое необходимо, чтобы потокосцепление достигло величины , то, подсчитывая такие площади для различных значений , мы получаем возможность построить зависимость
t f ,
которую удобнее изобразить, откладывая время по оси абсцисс, а потокосцепление по оси ординат (рис. 8.5, г). Это по существу и есть графическое изображение переходного процесса, иллюстрирующее закон нарастания потокосцепления во времени.
Пользуясь магнитной характеристикой катушки (рис. 8.5, б), полученную зависимость нетрудно перестроить в зависимость i f t . С этой целью для
ряда произвольных моментов времени t1,t2 ,...,ti ,..., выбранных на рис. 8.5, г, найдем соответствующие значения потокосцепления Ψ1, Ψ2 ,..., Ψi ,..., по которым, обращаясь к магнитной характеристике катушки, получим соответствующие значения i1,i2 ,...,ii ... токов. Отложив в определенном масштабе эти токи на рис. 8.5, г в надлежащие моменты времени, мы и получим искомую зависимость i f t .
Характерной особенностью переходного процесса при включении ферромагнитной катушки под постоянное напряжение является некоторое

Рис. 8.5. Включение ферромагнитной катушки под постоянное напряжение
затягивание нарастания тока в начале процесса по сравнению с показательной функцией, которой подчинялся аналогичный переходный процесс в катушке с постоянной индуктивностью L (рис. 4.7, б).
Включение ферромагнитной катушки под синусоидальное напряже-
ние. Возникающий при этом переходный процесс рассмотрим приближенно, полагая индуктивность катушки L постоянной величиной. Однако, чтобы не допустить слишком грубых приближений от полученного ранее дифференциального уравнения
L |
d i |
Ri u |
(8.26) |
|
d t |
||||
|
|
|
для тока i в цепи RL, мы, пользуясь известными соотношениями
Li или i L ,
перейдем к уравнению для потокосцепления
d |
|
R |
u . |
d t |
|
L |
|
(8.27)
(8.28)
Отличие последнего уравнения от первого заключается, в частности, в том, что здесь индуктивность L входит во второе слагаемое его левой части, в то время как в первом уравнении индуктивность является множителем первого слагаемого. По своему удельному весу в уравнении эти слагаемые не равноценны. Первое из них, представляющее собой ЭДС самоиндукции катушки, обычно на порядок больше второго, являющегося падением напряжения за счет резистивного сопротивления R обмотки. Поэтому допущение, что индуктивность L ферромагнитной катушки остается постоянной величиной, не зависимой от тока, во втором уравнении приведет к значительно меньшей погрешности в оценке переходного процесса, чем такое же допущение в первом уравнении.
Общее решение второго уравнения, являющегося при постоянных значениях индуктивности L катушки и сопротивления R ее обмотки линейным дифференциальным уравнением первого порядка, представится по общему правилу суммой
Ψ Ψ Ψ |
(8.29) |
установившегося потокосцепления Ψ и свободной составляющей потокосцепления , последнее из которых выражается показательной функцией
Aexp t , |
(8.30) |
где А — постоянная интегрирования; — корень характеристического уравнения
|
R |
0 , |
(8.31) |
|
L |
|
|
то есть величина |
|
|
|
R . |
(8.32) |
||
|
|
L |
|
Тогда, вводя по аналогии с цепью RL понятие о постоянной времени катушки
|
L |
, |
|
|
(8.33) |
|
|
|
|||
|
R |
|
|
|
|
для общего решения дифференциального уравнения окончательно получим |
|||||
Ψ Ψ Aexp |
t |
. |
(8.34) |
||
|
|||||
|
|
|
|
|
|
При синусоидальном напряжении на катушке |
|
||||
u Um sin t u |
(8.35) |
||||
ее установившееся потокосцепление также будет синусоидальной функцией
Ψ Ψm sin t u , |
(8.36) |
совпадающей по фазе с током катушки (мы пренебрегаем здесь потерями в магнитопроводе катушки), то есть отстающей от приложенного напряжения на угол .
Следовательно, общее решение уравнения можно переписать в виде
Ψ Ψ sin t |
u |
Aexp |
|
t |
. |
(8.37) |
|
||||||
m |
|
|
|
|
||
|
|
|
|
|||
Пренебрегая остаточным потокосцеплением катушки, положим, что до включения цепи потокосцепление было равно нулю. Поскольку потокосцепление, как и ток, не может измениться скачком, то начальным условием в этой задаче будет условие 0 0 . Используя его, находим постоянную интегрирования:
A Ψm sin u , |
(8.38) |
что позволяет окончательно записать выражение для потокосцепления при переходном процессе:
Ψ Ψ Ψ Ψm sin t u Ψm sin u exp |
|
t |
|
. (8.39) |
|
||||
|
|
|
|
|

Нетрудно убедиться, что это выражение полностью совпадает с полученным ранее выражением для тока переходного процесса при включении цепи RL под синусоидальное напряжение. Это позволяет, не повторяя подробно проведенные ранее исследования, сделать следующие заключения: во-первых, в начале переходного процесса возможно появление ударного потокосцепления Ψуд , превосходящего по величине амплитуду Ψm установившегося потокосце-
пления; во-вторых, величина ударного потокосцепления будет зависеть от момента включения цепи (от начальной фазы u напряжения); в-третьих, наибольшее значение ударного потока возникает при включении катушки в момент, когда фаза напряжения равна u 0,5 .
Если постоянная времени L / R катушки достаточно велика, то свободная составляющая Ψ потокосцепления затухает весьма медленно (рис. 8.6) и ударное потокосцепление Ψуд почти достигнет своего максимально возмож-
ного значения, равного удвоенной амплитуде установившегося потокосцепления.
При этом соответствующие значения ударного тока катушки могут достичь очень больших значений. Дело в том, что эксплуатация ферромагнитных катушек обычно проводится в режиме, когда амплитуда Ψm установившегося
потокосцепления приходится на колено магнитной характеристики катушки (рис. 8.7). В этом случае достигается достаточно большой магнитный поток катушки при умеренном значении амплитуды Im намагничивающего тока. Если
же в этих условиях ударное потокосцепление приобретает удвоенное значение 2Ψm , то намагничивающий ток катушки, обеспечивающий такое потокосцеп-
ление, оказывается несоизмеримо больше амплитуды Im установившегося тока катушки.
Рис. 8.6. Изменение потокосцепления при включении ферромагнитной катушки под синусоидальное напряжение

2
t
Im
Рис. 8.7. Магнитная характеристика катушки
Примерная картина переходного процесса при включении ферромагнитной катушки в случае неблагоприятного момента ее включения представлена на рис. 8.8. Через полупериод после включения катушки мгновенное значение намагничивающего тока достигает наибольшей величины, равной I уд , а в сле-
дующие периоды всплески намагничивающего тока постепенно уменьшаются, и кривая тока с течением времени приближается к кривой установившегося режима.
Ударный ток при включении ферромагнитных катушек под синусоидальное напряжение представляет для них серьезную опасность, так как в отдельных случаях всплески тока могут достигать колоссальных значений, в десятки и даже сотни раз превосходящих амплитуду установившегося тока. Такие токи вызывают огромные механические усилия между отдельными частями обмотки, приводящие иногда к ее повреждению или полному разрушению. Поэтому крупные ферромагнитные катушки с большой постоянной времени (большая индуктивность L при малом сопротивлении R обмотки) рекомендуется включать под переменное напряжение через токоограничивающие резисторы или с предварительным снижением напряжения до 50 %.

Ψуд Ψ
0
Iуд
Рис. 8.8 Картина переходного процесса для тока
С другой стороны, возможность возникновения больших ударных токов в ферромагнитных катушках должна предусматриваться и при их проектировании с целью создания конструкций с достаточным запасом механической прочности.
Заметим, что опасность тепловой перегрузки обмотки ударным током практически отсутствует, так как его действие весьма кратковременно.
8.7. Практическое использование нелинейных свойств электрических цепей в различных областях электротехники
Все изложенное в настоящей главе, а также в главе, посвященной нелинейным цепям постоянного тока, показывает исключительно широкие возможности, которые открываются при использовании нелинейных элементов для создания электрических цепей, обладающих самыми различными, весьма важными для практики свойствами.
Используя нелинейные элементы, можно осуществить стабилизаторы напряжения и тока, усилители мощности, модуляторы, детекторы, генераторы незатухающих колебаний, выпрямители, инверторы и т. д. Рассмотренными примерами далеко не исчерпывается перечень возможных применений нелинейных элементов в электрических цепях. Так, например, очень важным является создание устройств для формирования импульсов напряжения различной формы, создание так называемых спусковых устройств — триггеров, в которых используется неустойчивое состояние и при плавном изменении входного напряжения происходит скачок напряжения или тока на выходе и т. д.
Радиотехника, автоматика, телемеханика, электроизмерительная техника, техника электронных быстродействующих счетно-решающих и управляющих машин, электроэнергетика и другие области техники на современном этапе развития все шире используют особые свойства нелинейных цепей. Еще большие возможности открываются в этом направлении в будущем.
Вместе с тем изучение явлений в нелинейных системах представляет собой еще недостаточно разработанную и весьма интересную область для теоретических и экспериментальных исследований, хотя многое, как отмечалось, здесь уже сделано, причем весьма существенный вклад в разработку нелинейных проблем внесен российскими учеными.
Тесты для самопроверки
1.Метод, основанный на графическом подсчёте определенного интеграла применим к нелинейным электрическим цепям, описываемым дифференциальными уравнениями...
а. Первого порядка, допускающие разделение переменных. б. Второго порядка.
в. Третьего порядка.
г. Любого порядка без ограничений на переменные.
2.В методе условной линеаризации характеристика нелинейного элемента заменяется.
а. Только прямой линией.
б. Только отрезками прямых линий. в. Только экспоненциальной функцией.
г. Всеми указанными в пунктах а , б, в способами.
3.Метод кусочно-линейной аппроксимации позволяет ли перейти от нелинейного дифференциального уравнения к нескольким линейным дифференциальным уравнениям?
а. Нет. б. Да. в. Для ответа недостаточно данных.
4. Метод интегрируемой нелинейной аппроксимации основан на… а. Аппроксимации характеристики нелинейного элемента такой нелиней-
ной функцией, которая достаточно точно отображает его характеристику в
предполагаемом интервале перемещения изображающей точки по ней и дает возможность точно проинтегрировать уравнение в известных функциях.
б. Делении процесса на последовательные интервалы времени, внутри которых нелинейные уравнения заменяются линейными уравнениями с постоянными коэффициентами.
в. Линеаризации второстепенных членов уравнения, превращающей уравнение в линейное, с возможностью применения последовательных приближений.
г. Кусочно-линейной аппроксимации нелинейной характеристики ломаной прямой, для прямолинейных участков которой составляются и решаются линейные уравнения с последующим припасовыванием предыдущих и последующих участков.
5. Методом медленно меняющихся амплитуд рассчитывают… а. Мгновенные значения токов и напряжений б. Огибающие мгновенных значений токов и напряжений. в. Частотные характеристики г. Амплитудно-частотные характеристики.
6. Какой вид имеет искомая функция x(t) в методе медленно меняющихся амплитуд?
а. |
x asin t bcos t . |
б. x asin t b . |
в. x a bcos t . |
г. |
x sin t cos t . |
|
|
7.Амплитуда ударного тока при включении ферромагнитных катушек под синусоидальное напряжение может достигать значения…
а. В десятки раз превосходящая амплитуду установившегося тока.
б. Не более чем в три раза превосходящая амплитуду установившегося
тока.
в. Не более чем в два раза превосходящая амплитуду установившегося
тока.
г. Амплитуды установившегося тока.
8.Крупные ферромагнитные катушки с большой постоянной времени (большая индуктивность L при малом сопротивлении R обмотки) рекомендуется включать под переменное напряжение…
а. Только через токоограничивающие резисторы.
б. Только с предварительным снижением напряжения до 50 %. с. Через компенсирующий конденсатор.
г. Согласно условиям п. а и п.б.
ГЛАВА 9. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ |
С |
РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ |
|
9.1. Возникновение переходных процессов в цепях с распределенными параметрами
В цепях с распределенными параметрами, например с длинными линиями, обмотками электрических машин и трансформаторов и т. п., включение и отключение какого-либо участка (так же, как и в цепях с сосредоточенными параметрами) сопровождаются переходными процессами. При большой протяженности линий изменения внешних электрических и магнитных полей, например, при грозовых разрядах также вызывают переходные процессы. Переходные процессы в линиях возникают и при передаче телеграфных и телефонных сигналов, телемеханических импульсов или специальных импульсов для проверки линий и выявления места их повреждения.
Во всех случаях при анализе переходных процессов в цепях с распределенными параметрами необходимо исходить из общих закономерностей и дифференциальных уравнений.
Так как линия является наиболее распространенным примером цепи с распределенными параметрами, в дальнейшем изложении речь будет идти о переходных процессах в линиях.
9.2. Общее решение уравнений однородной неискажающей линии
Для выяснения наиболее характерных особенностей переходных режимов в однородных линиях найдем общее решение уравнений однородной линии:
u r i L |
i ; |
|
i |
g u C |
u |
|
t |
||||
x |
t |
|
x |
||
для частного случая неискажающей линии, когда r C g L . |
|
||||
Положим r / L g / C и введем вместо u и i новые функции u1 и i1 , |
|||||
связанные c u и i соотношениями |
|
|
|
|
|
u u1 exp t ; |
i i1 exp t . |
|
|||

Тогда имеем
u |
u1 exp t ; |
||
x |
|
x |
|
|
i |
|
i1 exp t ; |
|
x |
||
|
|
x |
|
u |
u1 exp t u |
|
exp t |
; |
||
t |
|
t |
1 |
|
|
|
|
|
|
|
|
||
i |
|
i1 exp t i |
exp t . |
|
||
t |
|
t |
1 |
|
|
|
|
|
|
|
|
||
Подставляя найденные значения производных в основные уравнения линии и сокращая на exp t , приведем их к виду
|
|
|
|
u1 |
L i1 |
; |
|
|
|
i1 |
C u1 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
x |
|
|
t |
|
|
|
|
|
x |
|
|
t |
|
|
|
|
|
|
|
|
||||
и, взяв производную от первого по х, а от второго по t , получим |
|
|
||||||||||||||||||||||||||
|
|
|
|
2 u |
|
|
2 i |
|
|
|
|
|
|
2 i |
|
|
2 u |
|
|
|
|
|
||||||
|
|
|
|
1 L |
|
1 |
; |
|
|
|
|
|
|
1 |
C |
|
|
1 . |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
x2 |
|
x t |
|
|
|
|
|
|
x t |
|
|
t2 |
|
|
|
|
|
||||||||
Отсюда найдем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 u |
L C |
2 u |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
и, положив CL 1/ v 2 , придем к волновому уравнению |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 u |
v2 |
2 u |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
1 . |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Введем вместо х и t новые переменные, а именно |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
x v t ; x v t . |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Тогда, приняв во внимание, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1; |
|
1; |
|
|
v ; |
|
v ; |
|
|
|
|
||||||||||||||
|
|
x |
|
|
t |
t |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
u1 |
u1 |
|
u1 ; |
|
u1 |
v u1 |
v |
u1 |
; |
|
|
|
|
|||||||||||||
|
|
x |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 u |
2 u |
|
2u |
|
2 u |
2 u |
|
v2 |
2 u |
2v2 |
|
|
2u |
v2 |
2 u |
|||||||||||||
1 |
1 |
2 |
|
1 |
|
|
|
1 ; |
|
|
1 |
|
1 |
|
|
1 |
|
1 |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
x2 |
2 |
|
|
2 |
|
t2 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|||||||||||
и подставив найденные значения вторых производных в волновое уравнение, найдем:
2u1 0 или u1 0 .
Отсюда, интегрируя, получим
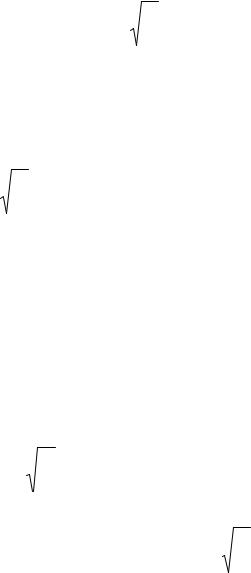
|
u1 |
|
и u1 d , |
||||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если положить d . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Возвращаясь к переменным х и t, можем написать: |
|
|
|
|
|
||||||||||||||||
|
|
|
|
u1 x vt x vt , |
|
|
|
|
|
|
|||||||||||
и, следовательно, для напряжения u между проводами линии имеем |
|||||||||||||||||||||
|
|
|
u1 [ x vt x vt ]exp t . |
|
|
|
|||||||||||||||
Для нахождения i |
подставим в уравнение |
i1 |
C |
u1 |
|
только что най- |
|||||||||||||||
|
|
||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
t |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
денное выражение для u1 . Тогда получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
i1 |
C |
|
|
|
|
|
|
|
||||||||||||
|
C |
|
|||||||||||||||||||
|
x |
|
|
t |
|
|
|
t |
|
|
t |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|||
|
|
|
C v |
|
|
|
, |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
L |
|
x |
|
|
x |
|
|
|
|
|||
так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
и |
|
|
|
, |
|
|
|
|
|
|
|||||
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||
и, проинтегрировав, найдем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
i C |
x vt x vt f t , |
|
|
|
||||||||||||||
|
|
|
1 |
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
потому что постоянная интегрирования не зависит от x , но может зависеть от t . Для определения f t подставим найденные для u1 и i1 значения в уравне-
ние u1 L i1 и тогда получим |
df t 0 . Следовательно, |
f t A const . |
||||
x |
t |
|
d t |
|
|
|
Однако можно положить A 0 , так как при A 0 мы могли бы ввести вместо |
||||||
и функции 1 0,5 A и 1 0,5 A, после чего получились бы выра- |
||||||
жения для u1 |
и i1 , в которые постоянная A не входит явно. Поэтому можем на- |
|||||
писать: |
|
|
|
|
|
|
|
i C |
x vt x vt |
|
|
|
|
|
1 |
L |
|
|
|
|
|
|
|
|
|
|
|
и, следовательно, для тока i в линии получим |
|
|
|
|||
|
i x vt x vt exp t : |
L |
, |
|
||
|
|
|
||||
|
|
|
|
C |
|
|

где |
L |
представляет собой, как известно из предыдущего, волновое сопротив- |
|
C |
|||
|
|
ление неискажающей линии.
Полученные выражения для напряжения u и тока i можно привести к иному виду, приняв во внимание, что
2 |
r |
|
g |
2v2 |
и t v t , |
|
L C |
||||||
|
|
|
||||
где r g — коэффициент затухания неискажающей линии, и что, следова-
тельно,
exp t exp v t exp x vt exp x exp x vt exp x .
На основании последних равенств выражения для u и i можно представить в виде
ux vt exp x x vt exp x ;
i x vt exp x x vt exp x :  CL ,
CL ,
причем следует иметь в виду, что функции и в этих выражениях отличаются от и в предыдущих выражениях для напряжения и тока соответственно множителями exp x v t и exp x v t .
9.3. Волны в неискажающей линии
Рассмотрим только что полученные нами выражения для напряжения и тока линии. При этом для простоты сначала допустим, что потери в линии пре-
небрежимо |
малы, |
т. |
е. |
положим |
r 0 |
и |
g 0. |
Тогда |
|
0, |
0, |
exp t 1, |
|
|
|
|
|
|
|
exp x vt exp x v t exp x exp x 1, |
для |
линии без |
потерь |
||||||
мы получим |
|
|
u x v t x v t ; |
|
|
|
|||
|
|
|
|
|
|
|
|||
i x vt :
Пусть в частном случае x vt
L |
|
|
|
|
|
L |
|
|
|
|
|
|
|
||
|
|
|
|
||||
C |
x vt : |
C |
. |
||||
|
|
|
|
|
|
||
0 |
и u x v t . Тогда, положив в по- |
||||||
следнем равенстве t 0 , мы найдем распределение напряжения вдоль линии в начальный момент времени. Возьмем некоторую произвольную точку х и предположим, что она перемещается вдоль линии со скоростью v , т. е. что ее поло-

жение определяется координатой x x0 v t . Тогда напряжение в этой движущейся точке u x0 vt vt x0 не будет зависеть от времени. Так как это заключение справедливо для любой точки, движущейся вдоль линии со скоростью v , то, следовательно, при u x v t начальное распределение напряжения и перемещается вдоль линии со скоростью v. Иными словами, при u x v t вдоль линии распространяется со скоростью v прямая волна напряжения, бегущая вперед и не претерпевающая изменения формы. Аналогично функция u x v t определяет обратную волну напряжения, распростра-
няющуюся вдоль линии также без изменения формы со скоростью ( v ) или, что то же самое, распространяющуюся со скоростью v в отрицательном направлении счета расстояний, т. е. бегущую назад.
Таким образом, при отсутствии потерь в линии напряжение, а также и ток в ней могут быть представлены как суммы двух волн, распространяющихся
вдоль линии без изменения формы со скоростью v 1/  LC в противоположных направлениях. При этом в любой точке линии отношение напряжения и тока для прямой волны равно
LC в противоположных направлениях. При этом в любой точке линии отношение напряжения и тока для прямой волны равно  L / C , т. е. волновому сопротивлению линии, зависящему только от параметров линии, а для обратной волны это отношение равно
L / C , т. е. волновому сопротивлению линии, зависящему только от параметров линии, а для обратной волны это отношение равно  L / C . При рассмотрении установившихся процессов уже указывалось, что скорость распространения волн в неискажающей однородной линии v 1/
L / C . При рассмотрении установившихся процессов уже указывалось, что скорость распространения волн в неискажающей однородной линии v 1/  LC для воздушных линий равна скорости света в воздухе.
LC для воздушных линий равна скорости света в воздухе.
Наличие в выражениях для u и i множителя exp t или соответственно в другом их выражении множителей exp x и exp x , причем r g ,
показывает, что обе волны по мере продвижения их вдоль линии затухают по показательному закону. Причиной затухания волн является постепенное превращение начального запаса энергии электрического и магнитного полей, связанных с линией, в тепло, выделяющееся в проводах, так как r 0 , а также и в среде, окружающей провода, так как g 0.
В дальнейшем мы будем предполагать, что волны при движении их вдоль линии не затухают. Затухание волн вследствие потерь в линии при необходимости может быть учтено, по крайней мере, для неискажающей линии, так как нами установлено, что в этом случае волны затухают по показательному закону
с показателем x r g x .
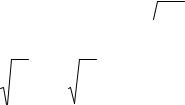
При наличии только одних прямых или только одних обратных волн для энергий магнитного и электрического полей на элементе d x , приняв во внима-
ние, что u2 / i2 L / C , найдем:
dWM 12 i2 L d x 12 u2C d x dWЭ .
Отсюда следует, что в каждом из этих случаев энергии магнитного и электрического полей на элементе длины линии, а следовательно, и во всей линии равны друг другу, и для суммы энергий этих попей на элементе линии получим
dW dWM dWЭ i2 L d x u2 C d x ui LC d x
LC d x
и для соответствующей мощности найдем:
p ui i |
2 L |
u |
2 |
C |
, |
|
|
C |
|
L |
|||
|
|
|
|
|
||
откуда следует, что при данном значении напряжения эта мощность тем больше, чем меньше волновое сопротивление линии.
9.4. О происхождении и характере волн в линиях
Возникновение волн в линиях обычно связано или с атмосферными разрядами, или с переключениями, т. е. с включением и выключением или самих линий, или устройств, связанных с ними.
Пусть в линии на некотором ее протяжении индуктирован заряд вследствие нахождения над этой частью линии заряженного облака. Если облако, индуктировавшее заряд, разрядится, то этот заряд освободится, и тогда напряжение вдоль линии будет распределено пропорционально заряду, приходящемуся на каждый элемент длины линии. В результате освобождения индуктированного заряда вдоль линии начнут распространяться волны напряжения и тока. Пусть распределение напряжения вдоль линии в начальный момент времени задано функцией f0 x (рис. 9.1, а). Волновое сопротивление линии, являющее-
ся в нашем случае вещественным числом, равным L / C , обозначим через z . Тогда, приняв во внимание, что ток в начальный момент времени равен нулю, имеем
u0 u 0 u 0 f0 x ;
i0 i 0 i 0 u 0 u 0 / z 0 ,
и, следовательно,

u 0 u 0 0,5 f0 x .
Рис. 9.1. Распределения напряжений вдоль линии при t 0
Таким образом, в начальный момент времени напряжение представляет собою сумму двух равных волн, одинаковых по форме и имеющих один и тот же знак, а ток — сумму двух волн, одинаковых по форме, но имеющих противоположные знаки.
С момента освобождения индуктированного заряда эти волны напряжения, а также и волны тока распространяются по линии в противоположных направлениях, причем скорости всех этих волн по абсолютной величине равны между собой. На рис. 9.1 представлены движения волн напряжения и тока в первые моменты времени после освобождения индуктированного заряда в предположении, что они не затухают.
При изучении явлений, связанных с переключениями, в тех случаях, когда длина линии мала по сравнению с длиной волны, мы будем предполагать, что внешние ЭДС постоянны. Это предположение допустимо, так как рассматриваемые явления протекают настолько быстро, что в случае синусоидальной ЭДС, имеющей частоту порядка десятков герцев, величина этой ЭДС за время пробега волны вдоль всей линии может измениться лишь весьма незначительно. Кроме того, можно считать, что процессы переключения осуществляются мгновенно. В соответствии с этими предположениями в дальнейшем примем,
что волны напряжения и тока, идущие от источника внешней ЭДС, имеют прямоугольную форму.
9.5. Преломление и отражение волн в месте сопряжения двух однородных линий
Пусть волна 1 бегущая от источника ЭДС по однородной линии, имеющей волновое сопротивление z1 достигла конца этой линии, в которой последняя соединена с другой однородной линией, имеющей волновое сопротивление z2 . Обозначив напряжение и ток в первой линии через u1 и i1, а во второй — через u2 и i2 , в месте сопряжения обеих линий имеем u1 u2 и i1 i2 . Предпо-
ложим, что во второй линии до прихода волны из первой линии напряжения не было. Тогда непосредственно после прихода волны к месту сопряжения линий во второй линии может возникнуть лишь волна 2 , бегущая в том же направле-
нии, что и волна 1, и называемая преломленной волной, в то время как в первой линии, кроме волны 1, называемой падающей волной, при z2 z1 обязательно возникнет волна 1 , бегущая в обратном направлении и называемая от-
раженной волной, так как иначе не могут быть удовлетворены условия равенства напряжений или токов в месте сопряжения линий. Поэтому, отмечая индексами 1, 1 и 2 соответственно падающие, отраженные и преломленные вол-
ны, в месте сопряжения линий имеем
|
|
|
|
|
u1 |
|
u 1 |
|
u |
u |
2 |
u2 ; |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i1 u 1 u 1 / z1 u 2 / z2 i2 , |
|
|
|
|||||||||||||||||||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
2 |
|
|
|
|
2z2 |
|
u |
1 |
; |
u |
2 |
|
z2 z1 |
u |
1 |
; |
|||||||||||||||
z |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
2 |
|
z |
|
|
|
|
|
|
|
|
|
z |
2 |
z |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
|
i |
|
|
|
|
|
|
2z1 |
|
|
|
i |
|
; |
i |
|
|
z1 z2 |
i |
. |
|
|||||||||||
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
2 |
|
|
|
|
2 |
z |
|
1 |
|
2 |
|
|
z |
2 |
z |
|
|
1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||
Из этих отношений следует, что в данном случае преломленные и отраженные волны имеют ту же форму, что и падающие волны. Отношения (u 2 / u 1) и (i 2 / i 2 ) можно рассматривать как коэффициенты преломления, а
отношения u 1 / u 1 qu и i 1 / i 1 qi — как коэффициенты отражения.
Из выражений, полученных для преломленных и отраженных волн, следует, что преломленные волны напряжения и тока имеют тот же знак, что и па-

дающие, а из отраженных волн одна сохраняет знак падающей волны, а другая имеет обратный знак.
При z1 z2 , что, например, имеет место при переходе волны из кабельной
линии в воздушную, преломленная волна напряжения больше падающей, а преломленная волна тока меньше падающей. Что касается отраженных волн, то волна напряжения отражается без перемены знака, а волна тока — с переменой знака, причем по абсолютной величине обе эти волны меньше соответствующих падающих волн. При этом вследствие наложения отраженных волн на падающие ток в первой линии уменьшается, а напряжение возрастает, но не более чем в два раза. На рис. 9.2 показаны падающие, преломленные и отраженные волны при z2 z1 . Заметим, что даже при очень больших значениях z2 пре-
ломленная волна напряжения не может превысить падающую волну более чем в два раза.
При z1 z2 преломленная волна напряжения меньше падающей, а пре-
ломленная волна тока больше падающей. В этом случае при отражении знак изменяется для волны напряжения, а абсолютные величины обеих отраженных волн опять будут меньше, чем величины соответствующих падающих волн. Вследствие наложения отраженных волн на волны падающие напряжения в первой линии уменьшаются, а ток возрастает, но не более чем в два раза (рис. 9.3). Заметим, что даже при очень больших значениях z2 преломленная волна
тока не может превысить падающую волну более чем в два раза.
Рис. 9.2. Падающие, преломленные и отраженные волны при z1 z2
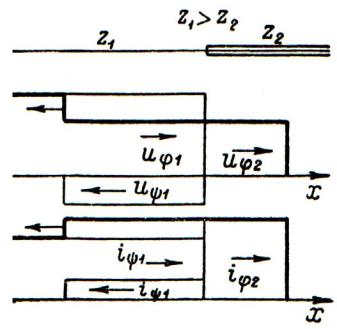
Рассматривая мощность p в месте сопряжения линий, имеем
|
|
|
|
p u1ii u2i2 |
|
|
|
|
||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u 1 |
u 1 |
|
u 1 u 1 |
|
u21 |
|
u21 |
|
u22 |
, |
||||||||
|
|
|
|
z1 |
|
|||||||||||||
|
|
|
|
z1 |
|
|
|
|
z1 |
|
|
|
|
z2 |
||||
и, следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u21 |
|
u21 |
|
|
u22 |
|
|
|
|
|||||
|
|
|
|
z |
z |
|
z |
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|||||
или
p 1 p 1 p 2 ,
где p 1, p 1, p 2 — мощности падающих отраженных и преломленных волн.
Отсюда следует, что часть мощности падающих волн, равная мощности преломленных волн, переходит во вторую линию, а остальная часть, равная мощности отраженных волн, возвращается обратно в первую линию.
Рис. 9.3. Падающие, преломленные и отраженные волны при z1 z2
Поэтому напряжение возрастает при переходе волны из кабельной линии в воздушную и из линий передачи в обмотки трансформаторов, которые представляют собой цепи, обладающие значительным волновым сопротивлением, превосходящим волновое сопротивление воздушных линий.
Волны, возникающие в линиях, распространяются с конечной скоростью и могут поэтому вызывать значительные перенапряжения между соседними точками цепи, в одну из которых волна напряжения уже пришла. Эти перенапряжения тем больше, чем круче фронт волны, и наиболее значительны при отвесном фронте волны. В связи с этим первые витки обмоток трансформаторов в соответствующих случаях выполняют со значительно усиленной изоляцией.
9.6. Отражение волн от конца линии
Пусть бегущие волны напряжения и тока достигли конца однородной линии, имеющей волновое сопротивление z и замкнутой на сколь угодно сложную цепь с сосредоточенными параметрами. В результате отражения падающих волн от конца линии возникнут отраженные волны , и для напряжения u и
тока i в конце линии, или, |
иными словами, для напряжения на зажимах око- |
|
нечной цепи и тока в ней получим |
|
|
u u u ; |
i i i u u / z ; |
z i u u , |
откуда |
|
|
|
2u zi u . |
|
Из этой простой зависимости следует, что ток i |
можно найти как ток, |
|
возникающий в эквивалентной схеме, включаемой под напряжение 2u и со-
стоящей из активного сопротивления, равного волновому сопротивлению z линии, и последовательно соединенной с ними оконечной цепью.
Определив ток i по заданным u , z |
и параметрам оконечной цепи, мож- |
||||||
но найти отраженные волны напряжения и тока из соотношений |
|||||||
u |
|
u |
|
z i ; |
i |
u |
. |
|
|||||||
|
|
|
|
z |
|
||
|
|
|
|
|
|
|
|
Рассмотрим, пользуясь этим способом, отражение волн от простейших оконечных цепей в предположении, что ЭДС источника падающих волн постоянна.
Пусть однородная линия с волновым сопротивлением z замкнута на сопротивление r0 . Тогда эквивалентная схема состоит из последовательно соеди-
ненных сопротивлений z и r0 , и мы имеем
|
2u |
|
|
|
|
|
r z |
|
|
|
|
|
u |
|
z r |
|
i |
|
; u |
|
u |
|
z i |
0 |
u |
|
; |
i |
|
|
|
0 |
i . |
z r |
|
|
r z |
|
z |
z r |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|

Таким образом, в рассматриваемом случае получены такие же соотношения между отраженными и падающими волнами, как и в случае отражения волн в месте сопряжения двух линий с той лишь разницей, что вместо волнового сопротивления второй линии вошло сопротивление r0 , на которое замкнута
линия.
При этом для мощности p u i в конце линии имеем
p ui u u |
u u |
|
u2 |
|
u2 |
p p , |
|
z |
z |
z |
|||||
|
|
|
|
т. е. эта мощность, поглощаемая приемником, равна разности мощностей падающих и отраженных волн. Если сопротивление r0 равно волновому сопро-
тивлению линии z , то отраженных волн не возникает и вся мощность падающих волн поглощается приемником.
Рис. 9.4. Отражение волн от конца линии
Из полученных выражений можно установить соотношение между падающими и отраженными волнами в случае отражения волн от конца разомкнутой или короткозамкнутой линии. При разомкнутой линии, полагая r0 , в конце линии имеем
u u ; |
i i , |
а при короткозамкнутой линии, полагая r0 0 , в конце линии получим
u u ; |
i i , |
т. е. в этих случаях отраженные волны имеют ту же величину, что и падающие, причем при разомкнутой линии с переменой знака отражается волна тока, а при короткозамкнутои линии с переменой знака отражается волна напряжения (рис. 9.4). Таким образом, в результате наложения отраженных волн напряжение на ее конце возрастает в два раза, а в короткозамкнутой линии ток в ее конце возрастает также в два раза, что можно получить из исследования отражения волн в месте сопряжения двух линий, полагая соответственно или z2 , или
z2 0.
Это можно пояснить следующим образом. И при холостом ходе, и при коротком замыкании падающие волны с присущей им энергией полностью отражаются от конца линии, так как в конце линии энергия не потребляется. Поэтому в той части линии, до которой дошли отраженные волны, энергия в два раза больше энергии падающих волн и, следовательно, в четыре раза больше энергии магнитного поля падающей волны тока, а также в четыре раза больше энергии электрического поля падающей волны напряжения, так как эти энергии равны друг другу.
При холостом ходе линии ток в ее конце должен равняться нулю. Поэтому, когда падающая волна тока придет к концу линии, то возникнет равная ей по величине и противоположная по знаку отраженная волна тока и ток в конце линии упадет до нуля, а энергия магнитных полей, связанных с падающей и отраженной волнами тока, перейдет в энергию электрического поля. Увеличение в конце линии энергии электрического поля в четыре раза повлечет за собой возрастание напряжения в конце линии в два раза. Это повышение напряжения, связанное с переходом энергии магнитного поля в энергию электрического поля, будет распространяться от конца линии к ее началу.
При коротком замыкании линии напряжение в ее конце должно равняться нулю. Поэтому, когда падающая волна напряжения придет к концу линии, то возникнет равная ей по величине и противоположная по знаку отраженная волна напряжения и напряжение в конце линии упадет до нуля, а энергия электрических полей, связанных с падающей и отраженной волнами напряжения, перейдет в энергию магнитного поля. Увеличение в конце линии энергии магнитного поля в четыре раза повлечет за собой возрастание тока в конце линии в два раза. Такое возрастание тока, связанное с переходом энергии электрического поля в энергию магнитного поля, будет распространяться от конца линии к ее началу.

Рассмотрим отражение волн в случае, когда конец однородной линии замкнут на цепь ( r0 , L0 ). Тогда эквивалентная схема состоит из последователь-
но соединенных сопротивления ( z r0 ) и индуктивности L0 , и при u const для тока i получим
|
|
|
|
|
|
|
|
|
|
|
i |
|
2u |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
exp |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
z r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
L0 |
|
, и для u |
|
и i найдём: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
z r0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
r |
z |
|
|
2 z |
|
|
t |
|
|
|
|
|
|
|
z r |
|
|
2 z |
|
|
t |
|
|||||||||
|
u |
|
|
|
0 |
|
|
|
exp |
|
|
|
u |
|
|
; |
i |
|
|
|
|
|
|
0 |
|
|
|
|
exp |
|
|
|
i . |
|||
|
|
r |
z |
r z |
|
|
|
r |
z |
r |
|
z |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|||||
Из этих выражений, положив t 0 , нетрудно усмотреть, что в первый момент отражение от цепи ( r0 , L0 ) происходит так же, как и от разомкнутого
конца линии. Полагая t , видим, что с течением времени напряжение и ток приближаются к значениям, которые ранее были получены для линии, замкнутой на сопротивление r0 . На рис. 9.5 показаны падающие и отраженные волны
для частного случая r0 0, когда:
|
|
|
z |
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
||
|
L |
|
L |
||||||
u 1 2exp |
t u ; |
i 1 2exp |
t i . |
||||||
|
|
|
0 |
|
|
|
|
0 |
|
Рассмотрим случай, когда волны отражаются от конца линии, замкнутой на цепь ( r0 , C0 ). Тогда эквивалентная схема состоит из последовательно
соединенных сопротивления ( z r0 ) |
и |
конденсатора емкостью C0 , и при |
|||||
u const для тока i мы имеем |
|
|
|
|
|
|
|
i |
2u |
|
|
t |
|
||
|
|
exp |
|
|
, |
||
z |
r0 |
|
|||||
|
|
|
|
|
|||
где (z r0 )C0 , и для u и i найдём:
u 1 r02 z z exp t u ; i 1 r02 z z exp t i .
Из этих выражений, положив t 0 , видим, что в первый момент времени отражение от цепи ( r0 ,C0 ) происходит так же, как в линии, замкнутой на со-
противление r0 . Полагая t , нетрудно убедиться, что с течением времени напряжение и ток приближаются к значениям, которые мы имели для случая

разомкнутой линии. На рис. 9.5 показаны падающие и отраженные волны для частного случая r0 0 , когда мы имеем
|
|
|
t |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
||||||
u 1 2exp |
|
u ; |
i 1 2exp |
|
i . |
||||
|
|
|
zC0 |
|
|
|
zC0 |
||
Так как до прихода отраженных волн к началу любой однородной линии напряжение на ее входных зажимах равно произведению тока в начале линии на ее волновое сопротивление, то изложенный способ определения отраженных волн пригоден и в тех случаях, когда к оконечной цепи с сосредоточенными параметрами присоединены те или иные однородные линии.
Рис. 9.5. Падающие и отраженные волны для случая r0 0
При этом, составляя соответствующую эквивалентную схему, каждую из линий, непосредственно присоединенных к оконечной цепи, следует заменить активным сопротивлением, равным ее волновому сопротивлению, независимо от того, что находится в конце этой линии. Необходимо, однако, иметь в виду, что составленная таким образом эквивалентная схема дает возможность производить расчеты лишь до момента прихода отраженных волн к началу хотя бы одной из линий, учтенных в этой схеме.
9.7. Процесс включения однородной линии
Рассмотрим процесс включения под синусоидальное напряжение однородной линии в предположении, что длина линии мала по сравнению с длиной волны. Тогда, как было указано выше, можно пренебречь затуханием волн в начальной стадии процесса включения, а также ограничиться рассмотрением включения линии под действие постоянного напряжения, равного мгновенному значению напряжения в начале линии в момент включения. Пусть, кроме того, внутреннее сопротивление генератора пренебрежимо мало, иными словами, мощность генератора весьма велика. При этом предположении волны напряжения и тока будут отражаться от генератора так, как они отражаются от короткозамкнутого конца линии.
Рассмотрим случай, когда включаемая линия разомкнута на приемном конце, и предположим, что до момента включения напряжение и ток по всей длине линии равны нулю. После включения от генератора вдоль линии начнут распространяться волны напряжения и тока, и, когда они дойдут до конца линии, напряжение вдоль линии будет равно напряжению генератора, а ток — напряжению генератора, деленному на волновое сопротивление линии. Дойдя до разомкнутого конца линии, эти волны отразятся, причем волна напряжения не изменит знака, а волна тока изменит знак. При движении к генератору отраженная волна напряжения, налагаясь на падающую волну, повышает напряжение в линии до удвоенного напряжения генератора, а отраженная волна тока уменьшает ток в линии до нуля. В тот момент, когда эти волны дойдут до генератора, ток по всей длине линии будет равен нулю, и вся линия будет заряжена до напряжения, равного удвоенному напряжению генератора. Волны, отразившиеся от разомкнутого конца, у генератора претерпят новое отражение, при котором волна напряжения изменит знак, а волна тока сохранит знак, так что получатся отрицательная волна напряжения и отрицательная волна тока, идущие от генератора к концу линии. Отрицательная волна напряжения при движении к концу линии понижает напряжение в линию до напряжения, равного напряжению генератора, и одновременно в линии возникает ток, противоположный по направлению первоначальному току. Дойдя до конца линии, отрицательные волны напряжения и тока претерпят третье отражение, в результате которого к генератору пойдет отрицательная волна напряжения, снижающая напряжение в линии до нуля, и положительная волна тока, уменьшающая ток в линии до нуля. Когда эти волны дойдут до генератора, линия будет полностью разряжена и

напряжение и ток по всей длине линии будут равны нулю. Этим и завершится полный цикл процессов, который при сделанных нами предположениях будет периодически повторяться. Отдельные характерные фазы рассмотренного цикла процессов представлены на рис. 9.6.
Полный цикл процесса движения и отражения волн в рассмотренном случае совершается в промежуток времени
T 4vl 4 l LC ,
где l — длина линии, a v — скорость распространения волн в ней. Этот промежуток времени Т называют периодом собственных колебаний линии. Если бы индуктивность и емкость линии были сосредоточены, то период T0 собствен-
ных колебаний такого контура из катушки с индуктивностью L l и конденсатора емкостью C l был бы
T 2 L l C l 2 l  LC ,
LC ,
т. е. в / 2 раза больше, чем Т.
Рис. 9.6. Фазы процесса включения однородной линии
Наличие потерь в линии ведет к тому, что волны напряжения и тока постепенно затухают, а величины напряжения и тока приближаются к тем значениям, которые они должны иметь при установившемся режиме холостого хода.
В случае включения линии, конец которой замкнут накоротко, волна напряжения, распространяющаяся от генератора, отражается от конца линии с пе-

ременой знака, а волна тока — без перемены знака. Отраженная волна напряжения, налагаясь на падающую волну, понижает напряжение в линии до нуля, а в результате наложения отраженной волны тока ток в линии удваивается.
Рис. 9.7. Процессы в однородной линии, замкнутой в конце накоротко
Когда отраженные волны дойдут до генератора, то напряжение во всей линии будет равно нулю, а ток — удвоенному первоначальному току. Так как при всех последующих отражениях и от генератора, и от коротко-замкнутого конца линии волна напряжения отражается с переменой знака, то напряжение в линии изменяется между нулем и напряжением генератора. Отражение волны тока и от генератора, и от короткозамкнутого конца линии каждый раз происходит без перемены знака. Поэтому ток в линии после каждого отражения возрастает на величину первоначального тока (рис. 9.7).
Наличие потерь в линии вызывает затухание волн и ограничивает нарастание тока. По мере затухания волн напряжение и ток приближаются к тем значениям, которые они должны иметь при установившемся режиме короткого замыкания.
Если длина линии сравнима с длиной волны, то за время каждого пробега волны вдоль линии напряжение на зажимах генератора в начале линии успевает заметно измениться. При рассмотрении процессов в линии это изменение должно быть принято во внимание.
9.8.Прохождение волн при наличии реактивного сопротивления
вместе сопряжения однородных линий

Пусть между двумя однородными линиями с волновыми сопротивлениями z1 и z2 включена последовательно реактивная катушка с индуктивностью
L0 . Тогда, пренебрегая емкостью между витками обмотки катушки, в месте сопряжения линий имеем
i1 i2 ; u1 L0 ddit2 u2
и в случае перехода волн напряжения и тока из первой линии во вторую можем написать:
|
|
|
|
|
|
|
u 1 u 1 |
|
|
u 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
d u 2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
u 1 u 1 |
0 |
|
|
|
|
|
|
|
|
|
|
u 2 , |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
z1 |
|
|
z2 |
|
|
|
|
|
|
z2 |
|
|
d t |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
d u 2 |
|
|
z |
2 |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2u 1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
u 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
d t |
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
При прямоугольной форме падающей волны имеем u 1 const |
|
и, следо- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2z |
2 |
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2z |
|
|
|
|
|
|
|
t |
|
|
|
||||||||||||||
u |
|
|
|
|
|
1 |
exp |
|
|
|
|
|
|
u |
|
|
|
; i |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 exp |
|
|
|
|
i |
|
, |
||||||||||||||||||||
|
z |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
z |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где L0 / z1 z2 , и тогда для u 1 |
и i 1 найдем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
z |
2 |
|
z |
|
|
|
|
|
|
|
2 z |
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
exp |
|
|
|
|
|
u |
|
|
; |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
z |
|
z |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
z |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
z |
2 |
|
|
|
|
|
|
2 z |
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
exp |
|
|
|
|
|
i |
|
. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
z |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
z |
2 |
|
z |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Из полученных выражений видно, что в рассматриваемом случае прелом- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ленные волны u 2 |
|
и i 2 нарастают постепенно от значений, равных нулю при |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
t 0 , до значений, которые мы имели в случае отсутствия реактивной катушки. Что же касается отраженных волн u 1 и i 1 , то в первый момент они имеют та-
кие же значения, как при отражении от разомкнутого конца линии, а затем постепенно приближаются к значениям, которые мы имели при отсутствии катушки. Таким образом, в результате включения реактивной катушки фронт преломленных волн приобретает пологий характер даже при отвесном фронте падающих волн. Быстрота нарастания напряжения и тока во второй линии тем

меньше, чем больше постоянная времени L0 / z1 z2 , т. е. тем меньше, чем
больше индуктивность катушки. Сглаживание фронта преломленных волн в данном случае объясняется тем, что энергия падающей волны частично переходит в энергию магнитного поля, связанного с реактивной катушкой. Применяя реактивные катушки для сглаживания фронта преломленных волн, следует иметь в виду, что в результате наложения отраженной волны на падающую волну напряжение в первой линии в первые моменты времени удваивается.
На рис. 9.8 показаны падающие, преломленные и отраженные волны для частного случая z1 z2 , когда мы имеем
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
t |
|
||||||
u 2 |
1 exp |
|
|
|
|
u 1 |
; |
i 2 |
1 |
exp |
|
|
i 1 |
; |
||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
u |
|
exp |
t |
u |
|
; |
|
i |
exp |
|
t |
|
i |
|
, |
|
|||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|||||||
где L0 / 2 z1 L0 / 2 z2 .
Пусть в месте сопряжения линий включено ответвление, содержащее конденсатор, емкость которого равна C0 . Тогда в месте сопряжения линий имеем
u1 u2 ; i C0 ddut2 i2
и в случае перехода волн напряжения и тока из первой линии во вторую можем написать:
u 1 u 1 u 2 ; |
|
|
u 1 u 1 |
C0 |
|
d u 2 |
|
u 2 |
, |
|||||||||
|
|
z |
|
|
|
|
d t |
|
z |
2 |
||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
и, следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d u 2 |
|
z |
2 |
z |
|
|
|
|
|
|
||||
2u |
1 |
z C |
|
|
|
|
|
|
1 |
u |
2 |
. |
|
|
|
|
||
|
|
d t |
|
|
|
|
|
|
|
|||||||||
|
1 |
0 |
|
|
|
|
z2 |
|
|
|
|
|
||||||

C0
Рис. 9.8. Падающие, преломленные и отраженные волны для |
|
|
|
|
част- |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ного случая z1 z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
При прямоугольной форме падающей волны и u 1 |
const , и мы получим |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2z |
2 |
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
2z |
|
|
|
|
|
|
|
|
t |
|
|
|
|
||||||||
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
1 |
exp |
|
|
|
|
u |
|
|
; |
i |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
exp |
|
|
|
i |
|
|
||||||||||||
|
|
|
|
|
|
|
z |
|
z |
|
|
|
|
|
|
|
|
|
z |
|
z |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где |
|
|
z1z2 |
|
|
C0 , и тогда для u 1 |
и i 1 найдем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
z1 z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
z |
2 |
z |
|
|
|
|
2 z |
2 |
|
|
|
t |
|
|
|
|
|
|
z z |
2 |
|
|
|
|
2 z |
2 |
|
|
|
|
t |
|
|
|||||||||||||||||
|
u |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
exp |
|
|
|
u |
|
|
; i |
|
|
|
1 |
|
|
|
|
|
|
|
|
exp |
|
|
i |
. |
||||||||||||||
|
|
z |
|
z |
z |
|
|
z |
|
|
|
|
|
|
z |
|
z |
|
z |
|
|||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
2 |
|
|
2 |
|
|
|
|
|
1 |
1 |
|
z |
2 |
|
|
|
2 |
|
|
|
|
1 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||
Выражения, полученные для u 2 и i 2 , аналогичны выражениям, полу-
ченным в предыдущем случае, и в соответствии с этим преломленные волны нарастают постепенно от нуля до тех значений, которые они имеют при отсутствии ответвления. При этом быстрота их нарастания, определяемая постоян-
ной времени |
z1z2 |
C0 , тем меньше, чем больше емкость конденсатора C0 . |
|
|
|||
|
z1 z2 |
|
|
Что касается отраженных волн u 1 |
и i 1 , то в первый момент времени они име- |
||
ют такие же значения, как при отражении от короткозамкнутого конца линии, а
затем постепенно приближаются к значениям, которые мы имели при отсутствии ответвления.
Таким образом, в результате наличия емкостного ответвления фронт преломленных волн, как и в предыдущем случае, приобретает пологий характер даже при отвесном фронте падающих волн. Сглаживание фронта преломленных волн в данном случае объясняется тем, что энергия падающей волны частично переходит в энергию электрического поля конденсатора.
При применении емкостного ответвления для сглаживания фронта преломленных волн отраженная волна напряжения в первый момент времени равна по величине и противоположна по знаку падающей волне, и напряжение в первой линии в момент прихода волны к месту сопряжения линий падает до нуля, а затем постепенно нарастает. На рис. 9.8 показаны падающие, преломленные и отраженные волны для частного случая z1 z2 , когда мы имеем
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
t |
|
||||||
u 2 |
1 exp |
|
|
|
u 1 |
; |
i 2 |
1 |
exp |
|
|
i 1 |
; |
||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
u |
|
exp |
|
t |
u |
|
; |
i |
|
exp |
|
t |
i |
. |
|
|||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
1 |
|
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
||||||||
9.9. Прохождение волн при наличии активного сопротивления в месте сопряжения однородных линий
Пусть между двумя однородными линиями с волновыми сопротивлениями z1 и z2 включено последовательно с ними активное сопротивление r0 . Тогда в месте сопряжения линий имеем
i1 i2 ; u1 r0i2 u2 ,
и в случае перехода волны u 1 из первой линии во вторую можем написать:
|
u 1 u 1 |
|
u 2 |
|
|
|
|
|
|
|
|
r |
|
d u 2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
; |
|
|
u 1 |
u 1 |
|
|
0 |
|
|
|
u 2 , |
|||||
|
|
|
z1 |
|
|
z2 |
|
|
z2 |
|
d t |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и, следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
2 |
|
|
|
2z2 |
|
u |
1 |
; |
u |
1 |
|
z2 z1 r0 |
u |
1 |
. |
||||||||
z |
|
z r |
|
|||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
z |
2 |
z |
r |
|
|
||||||||||
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|||
Из этих выражений видно, что наличие сопротивления r0 уменьшает пре-
ломленную волну напряжения и что даже при большом значении , увеличи-
z 2
вая r0 , ее можно довести до сколь угодно малой величины. Отраженная волна
u 1 при z2 z1 с увеличением r0 возрастает, но не может превзойти величину u 1.
Мощность, выделяющаяся в сопротивлении |
|
r , |
равна |
p r i2 |
|
r0 |
|
u2 |
, в то |
|||||||||||||
|
z22 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 2 |
|
2 |
|
||
время как мощность падающей волны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
p 1 |
|
u21 |
|
. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
z1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для отношения этих мощностей имеем |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
p |
|
|
r z |
u2 |
2 |
|
|
|
|
4r z |
|
|
|
|
|
|
||||
|
|
|
|
|
0 1 |
|
|
|
|
|
|
|
|
|
0 |
1 |
, |
|
|
|
|
|
|
|
p 1 |
z2 |
u2 |
|
|
z |
2 |
z r 2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2 |
|
1 |
|
|
|
|
1 |
0 |
|
|
|
|
|
|
||||
причем при |
r0 z2 z1 это |
|
отношение |
достигает |
максимума, |
равного |
||||||||||||||||
z1 /(z2 z1) . |
Таким образом, значительная часть мощности падающей волны |
|||||||||||||||||||||
может быть поглощена сопротивлением r0 лишь при z1 z2 , т. е. когда преломленная волна напряжения мала по сравнению с падающей. Однако при любом соотношении между z1 и z2 , взяв r0 z2 z1 , мы получим
u 2 |
|
|
z2 |
|
u 1, и тогда преломленная волна напряжения будет в два раза |
z |
z |
2 |
|||
|
1 |
|
|
||
меньше, чем при отсутствии сопротивления r0 (рис. 9.9).
Для того чтобы перенапряжения, возникшие на одном участке линии, не распространялись по всей ее длине, между отдельными участками линии включают активные сопротивления, уменьшающие, как мы только что видели, величину волн напряжения при их прохождении из одного участка в другой.

Рис. 9.9. Падающие, преломленные и отраженные волны для частного случая r0 z2 z1
Так как для эффективного действия эти сопротивления должны иметь величину порядка 500 − 600 Ом, то параллельно с ними включают реактивные катушки, имеющие незначительное сопротивление для тока нормальной частоты, но оказывающие в первые моменты значительное сопротивление волнам.
Пусть теперь в месте сопряжения линий включено ответвление, имеющее только активное сопротивление r0 . Тогда в этом месте
u1 u2 ; i1 u2 i2 , r0
и в случае перехода волны u 1 из первой линии во вторую можем написать:
|
|
u 1 u 1 u 2 ; |
|
u 1 |
u 1 |
|
|
|
u 2 |
|
u |
2 |
|
|
|
|
|||||||||||||||
|
|
|
|
z1 |
|
|
|
|
|
r0 |
|
z2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
и, следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
2 |
z |
|
z |
2 z1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
u |
|
|
|
|
2z2 |
|
|
|
u |
|
; |
|
u |
|
|
|
|
|
1 |
|
|
|
|
r0 |
u |
|
. |
||||
2 |
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
||||||||||||
|
|
|
z |
z |
|
|
|
|
|
|
|
|
|
|
|
z |
z |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
z |
2 |
z |
|
2 1 |
|
|
|
|
|
|
|
|
|
|
z |
2 |
z |
|
|
2 1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
1 |
|
r0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
r0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Из этих выражений вытекает, что наличие активного ответвления уменьшает преломленную волну напряжения, причем, уменьшая r0 , ее можно дове-
сти до сколь угодно малой величины. Отраженная волна u 1 с уменьшением r0 возрастает по абсолютной величине, но не может превзойти величину u 1.
Мощность, выделяемая в ответвлении, |
равна |
p |
|
u2 |
2 |
, в то время как |
||||||||||||
|
r |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
мощность падающей волны p 1 |
|
u21 |
|
. Для отношения этих мощностей имеем |
||||||||||||||
|
z1 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
p |
|
z |
|
u2 2 |
|
|
4z z2 |
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
1 2 |
|
|
|
|
|
, |
|
|
|
p 1 |
r0 |
|
u2 |
|
|
z1z2 |
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
r0 z2 |
z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
причем при r0 z1z2 /(z1 z2 ) |
это отношение достигает максимума, равного |
|||||||||||||||||
z1z2 /(z1 z2 ). Таким образом, в рассматриваемом случае при z1 z2 , когда
преломленная волна напряжения значительно превосходит падающую, большая часть мощности последней поглощается в активном ответвлении. При этом, взяв r0 z1z2 /(z1 z2 ) , мы получим u 2 z2 / z1 z2 u 1, и тогда при любом соотношении между z1 и z2 преломленная волна напряжения будет в два раза
меньше, чем при отсутствии ответвления (рис. 9.10).
Во избежание прохождения через ответвление сколь-нибудь значительного тока при нормальной работе линии последовательно с сопротивлением r0
включают конденсатор, не оказывающий существенного сопротивления прохождению через него волн, но имеющий достаточно большое сопротивление для тока нормальной частоты.
r0 z1z2 /(z1 z2 ) .

Рис. 9.10. Падающие, преломленные и отраженные волны для случая
В заключение отметим, что для анализа переходных процессов в линиях с распределенными параметрами можно воспользоваться операторным методом. В случае применения операторного метода к анализу переходных процессов в цепях с сосредоточенными параметрами, как мы видели, обыкновенные дифференциальные уравнения для оригиналов переходят в алгебраические уравнения для их изображений. Соответственно применение этого метода к исследованию процессов в линиях с распределенными параметрами приводит к замене дифференциальных уравнений в частных производных для действительных токов и напряжений обыкновенными дифференциальными уравнениями для их операторных изображений.
Тесты для самопроверки
1. Какие линии электропередач считаются линиями с распределенными параметрами? Это такие цепи, у которых:
а. Физическая длина меньше длины волны. б. Физическая длина больше длины волны. в. Расстояние между проводами меньше длины волны. г. Расстояние между проводами больше длины волны.
2. Укажите дифференциальное уравнение для мгновенного значения напряжения в любой точке линии.

|
u |
i |
|
i |
|
i |
u |
г. iC C |
uC |
||
а. |
x iR L t . |
б. uL |
L t . |
в. |
|
iG C |
t . |
|
|
||
x |
t |
|
|||||||||
3. |
Телефонная линия обладает |
параметрами R = 10 Ом/км; |
g = 5·10-6 ; |
||||||||
C = 5·10-9 Ф/км. Определите величину |
индуктивности L, Гн/км, |
если линия |
|||||||||
является неискажающей. |
|
|
|
|
|
|
|
|
|||
|
0,1. |
0,01. |
0,001. |
0,2. |
|
|
|
|
|
|
|
|
а. |
б. |
в. |
г. |
|
|
|
|
|
|
|
4. При переходе волны из кабельной линии в воздушную линию возникает преломленная волна напряжения, которая распространяется…
а. По кабельной линии по направлению к воздушной.
б. По кабельной линии по направлению от ее конца к ее началу. в. По воздушной линии от места соединения с кабельной линией.
г. По воздушной линии от ее конца к месту соединения с кабельной ли-
нией
5. Величина |
L |
называется: |
|
C |
|||
|
|
а. Коэффициентом затухания; б. Коэффициентом фазы;
в. Коэффициентом распространения; г. Волновым сопротивлением.
6. Какие линии называются однородными?
а. Линии, у которых параметры распределены равномерно по их длине. б. Линии, у которых параметры распределены неравномерно по их длине.
в. Линии, которые описываются однородными дифференциальными уравнениями.
г. Линии, у которых параметры все линейные.
7. Если однородная линия с волновым сопротивлением z замкнута на сопротивление r0 , которое равно волновому сопротивлению линии z , то…
а. Отраженных волн не возникает и вся мощность падающих волн поглощается приемником.
б. Мощность, поглощаемая приемником, равна разности мощностей падающих и отраженных волн.
в. Мощность, поглощаемая приемником, равна мощности отраженных волн.
