
- •ГЛАВА 2. НЕЛИНЕЙНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА
- •ГЛАВА 3. НЕЛИНЕЙНЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- •ГЛАВА 8. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ЦЕПЯХ
- •Введение
- •ГЛАВА 11. Моделирование процессов в электрических цепях
- •Правильные ответы на вопросы тестов к главам 1 –9
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •Предметный указатель
СЕВЕРО-ЗАПАДНЫЙ ГОСУДАРСТВЕННЫЙ ЗАОЧНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
С.М. Аполлонский, А.Л. Виноградов
Теоретические основы электротехники. Линейные и нелинейные цепи.
Переходные процессы
Санкт-Петербург
2010
Министерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего профессионального образования
СЕВЕРО-ЗАПАДНЫЙ ГОСУДАРСТВЕННЫЙ ЗАОЧНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
С.М. Аполлонский, А.Л. Виноградов
Теоретические основы электротехники. Линейные и нелинейные цепи.
Переходные процессы
УЧЕБНОЕ ПОСОБИЕ
Санкт-Петербург Издательство СЗТУ
2010
Утверждено редакционно-издательским советом университета
УДК 621.3.011(075.8)
Аполлонский С. М. Теоретические основы электротехники. (Линейные и нелинейные цепи. Переходные процессы). учебное пособие /С.М.
Аполлонский, А.Л. Виноградов. – СПб.: Изд-во, 2010. – 377 с.
Учебное пособие разработано в соответствии с требованиями государственных образовательных стандартов высшего профессионального образования для специальностей: 140601.65 – «Электромеханика», 140602.65 – «Электрические и электронные аппараты», 140211.65 – «Электроснабжение», 210106 – «Промышленная электроника» и направлениям подготовки бакалавра: 140200.62 – электроснабжение, 140600.62 – электротехника, электромеханика и электротехнологии, 210100.62. – электроника и микроэлектроника.
Рецензенты: Ю.П. Коськин, д-р техн. наук, засл. деят. науки и техники РФ, проф. кафедры электромеханики и электромеханотроники ГЭТУ (ЛЭТИ); К.Р. Малаян, канд. техн. наук, проф. кафедры безопасности
жизнедеятельности СПбГПУ; В.Л. Беляев, д-р техн. наук, проф. кафедры электротехники и электромеханики СЗТУ.
©Северо-Западный государственный заочный технический университет, 2010
©Аполлонский С.М., Виноградов А.Л., 2010
ПРЕДИСЛОВИЕ
Учебное пособие "Теоретические основы электротехники. Линейные и нелинейные цепи» состоит из следующих основных разделов: теория линейных электрических цепей при периодических несинусоидальных напряжениях и токах; магнитные цепи; теория переходных процессов в линейных цепях, теория установившихся и переходных процессов в нелинейных цепях; компьютерное моделирование электрических цепей.
Цель дисциплины - формирование системы научных знаний по этим разделам дисциплины ТОЭ, умения использовать полученные знания для решения практических задач электротехники.
В результате изучения дисциплины ТОЭ студент должен знать: теорию линейных электрических цепей при периодических несинусоидальных напряжениях и токах, и в переходных процессах при различных видах входного воздействия; теорию установившихся и переходных процессов в нелинейных цепях постоянного и переменного токов; методы расчета установившихся и переходных процессов в линейных и нелинейных цепях, в том числе с применением ЭВМ.
Уметь- рассчитывать установившиеся режимы в линейных цепях при несинусоидальных токах и напряжениях на базе комплексного метода расчета; проводить инженерный расчет переходных процессов классическим, операторным, частотным методами, а также методом переменных состояния с численным интегрированием дифференциальных, уравнений с помощью ЭВМ; рассчитывать нелинейные электрические и магнитные цепи постоянного тока графическими и аналитическими методами; рассчитывать нелинейные цепи при периодических процессах и в переходных режимах аналитическими и численными методами с применением ЭВМ и уметь анализировать устойчивость установившихся режимов.
Связь с другими дисциплинами. При изучении курса ТОЭ необходимы знания следующих дисциплин и их разделов:
по физике - электричество и магнетизм, колебания и волновое движение, физика твердого тела, физические величины и единицы их измерения; по высшей математике - дифференциальное и интегральное исчисления, диф-
ференциальные уравнения и методы их решения; операционное исчисление, ряды, функции комплексной переменной, элементы теории устойчивости;
по метрологии и стандартизации - Международная система единиц (СИ); методы и средства измерения электрических и магнитных величин; оценка погрешности; условные графические изображения электрических, магнитных и полупроводниковых элементов; схемы и их выполнение; по экономике - экономические критерии в электротехнике, повышение коэф-
фициента полезного действия и коэффициента мощности электротехнических устройств, надежность.
ВВЕДЕНИЕ
Впредлагаемом учебном пособии рассматриваются вопросы, связанные с теорией и методами расчета установившихся несинусоидальных процессов, линейных и нелинейных цепей в установившимся и переходном процессах, цепей
сраспределенными параметрами; компьютерными технологиями моделирования электрических цепей.
Учебное пособие включает три части и содержит 11 глав, расположенных в последовательности, соответствующей возрастающей сложности.
Впервой части, включающей четыре главы, рассмотрены несинусоидальные периодические процессы в линейных электрических цепях, а также статические и квазистатические процессы в нелинейных электрических цепях с сосредоточенными параметрами.
Во второй части, включающей пять глав, рассмотрены переходные процессы в электрических цепях с сосредоточенными и распределенными параметрами.
Рассмотрение материала в первых двух частях пособия приводится традиционным способом, как это принято в электротехнической литературе. Не все из этих глав обязательны к изучению в полном объеме. В зависимости от специальности некоторые из них моно изучать частично.
Втретей части пособия, включающей две главы, студентам предлагается материал по компьютерному моделированию электрических цепей. Поскольку книга имеет учебный характер, в качестве основного инструментария авторами выбрана программа Multisim, отличающаяся простым и легко усвояемым пользовательским интерфейсом. Многие студенты уже знакомы с этой программой по материалам отечественных и зарубежных авторов, использующих в своих
пособиях учебных пособиях программу Multisim. Следует отметить, что более ранние версии этой программы назывались Elektronics Workbench (EWB).
Все главы пособия заканчиваются тестами для самопроверки. При количестве правильных ответов не менее 60 % уровень подготовки по изученной главе можно считать удовлетворительным. Ответы на вопросы теста по каждой главе приведены в конце пособия.
Отобранный для пособия учебный материал дает студенту возможность в дальнейшем успешно осваивать специальные дисциплины. Все теоретические выкладки имеют подробные пояснения, что помогает студенту самостоятельно разобраться в их последовательности и оценить полученный результат. Большое внимание в пособие уделено на связь между теоретическими результатами и их практическим применением в промышленности.
ЧАСТЬ I. НЕСИНУСОИДАЛЬНЫЕ ПЕРИОДИЧЕСКИЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЦЕПЯХ.
ТЕОРИЯ НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ СТАТИЧЕСКИХ ПРОЦЕССАХ
ГЛАВА 1. ЛИНЕЙНЫЕ ЦЕПИ ПРИ НЕСИНУСОИДАЛЬНЫХ ТОКАХ 1.1. Основные понятия о приемах расчета цепей
Несинусоидальные ЭДС, напряжения и токи. Несинусоидальными ЭДС, напряжениями и токами принято называть такие из упомянутых величин, которые изменяются во времени по произвольному периодическому закону, отличающемуся от синусоидальной функции.
Несинусоидальные токи могут возникнуть в электрических цепях или вследствие несинусоидальности ЭДС источников энергии, или из-за нелинейности отдельных элементов электрической цепи. В пределах настоящей главы мы остановимся на анализе только линейных цепей, несинусоидальные токи в которых возникают лишь под воздействием несинусоидальных ЭДС или несинусоидальных питающих напряжений.
Эксплуатация электрических цепей при несинусоидальных напряжениях и токах, как правило, является нежелательной, так как влечет за собой снижение эффективности использования электротехнического оборудования. Тем не
менее, с такими режимами нередко приходится встречаться на практике, поскольку обеспечить строго синусоидальные ЭДС или напряжения источников удается далеко не всегда. Поэтому вопросы расчета линейных цепей при действии в них несинусоидальных ЭДС или напряжений представляют большой интерес.
Идея расчета линейных цепей при несинусоидальных ЭДС. Из курса математики известно, что всякую периодическую функцию определенной частоты можно разложить в гармонический ряд (ряд Фурье), то есть на сумму синусоидальных функций кратных частот. Если такое разложение применить к несинусоидальной ЭДС источника, питающего линейную цепь, то задачу о ее расчете можно, прибегая к методу наложения, расчленить на ряд частичных задач, в каждой из которых в цепи будет действовать лишь одна синусоидальная ЭДС той или иной частоты. После решения отдельных частичных задач результирующие токи в ветвях определяются путем суммирования соответствующих частичных токов, представляющих собой также синусоидальные токи кратных частот. Этим приемом удается свести расчет электрической цепи при несинусоидальной ЭДС или несинусоидальном питающем напряжении к уже известным методам расчета таких цепей при синусоидальных ЭДС или напряжениях. Естественно, что точное решение задачи таким приемом возможно лишь в случае, когда ЭДС источника или питающее напряжение разлагаются в ряд Фурье с конечным и притом с относительно небольшим числом членов. Если же разложение питающего напряжения приводит к бесконечному ряду, то расчет цепи приходится ограничивать определенной точностью, обрывая ряд на том или ином члене.
1.2. Основы гармонического анализа
Ряды Фурье. В электротехнике наиболее удобной формой гармонического ряда, в который может быть разложена всякая практически встречающаяся периодическая функция времени v f t , является форма с начальными фазами
v V0 V1m sin t v |
V2m sin 2 t v |
... Vkm sin |
k t v ..., (1.1) |
|
|
1 |
2 |
|
k |
в |
которой член |
V0 называют |
постоянной |
составляющей, член |
v1 |
V1m sin t v1 , имеющий частоту, равную частоте разлагаемой функции, |
|||
именуют основной волной, или первой гармоникой, а все остальные члены вида vk Vkm sin k t vk , частота которых в целое число k раз больше частоты

данной функции, носят названия высших гармоник и в наименовании отличаются друг от друга порядковым номером k (вторая гармоника, третья гармоника и т. д.).
Если в выражениях для гармоник развернуть синусы сумм по известной формуле тригонометрии
sin x y sin xcos y sin y cos x ,
то общий член ряда представится в виде
vk Vkm sin k t vk Vkm cos vk sin k t Vkm sin vk cosk t
или, вводя обозначения
Ak Vkm cos vk , |
Bk Vkm sin vk , |
(1.2) |
получим
vk Ak sin k t Bk cosk t .
Используя полученное выражение, весь ряд, в целом, можно записать в форме без начальных фаз:
v V0 A1 sin t A2 sin 2 t ... |
Ak sin k t... |
B1 cos t B2 cos2 t ... |
Bk cosk t ..., |
|
(1.3) |
получившей распространение в математике.
Обратный переход от второй формы ряда Фурье к первой выполняется по формулам
V |
A2 |
B2 |
, |
tg |
vk |
|
Bk |
, |
(1.4) |
|
|||||||||
km |
k |
k |
|
|
|
Ak |
|
|
|
|
|
|
|
|
|
|
|
|
вытекающим из ранее принятых формул (1.2) перехода от первой формы ряда ко второй.
Формулы разложения. Математикой предлагаются следующие формулы для определения коэффициентов разложения периодической функции v f t в ряд Фурье при второй форме его записи:
|
1 T |
|
2 T |
2 T |
||||
V0 |
|
v d t , Ak |
|
|
vsin k td t , Bk |
|
vcosk td t , |
|
T |
T |
T |
||||||
|
0 |
|
0 |
0 |
||||
|
|
|
|
|
|
|||
причем угловая частота первой гармоники выражается через частоту f или период Т разлагаемой функции известной формулой:
2 f 2 T1 .
Если в разлагаемой функции за аргумент принять не время t, а пропорциональный ему угол t , то формулы разложения представятся в виде

|
1 T |
1 T |
1 T |
|
V0 |
|
v d , Ak |
vsin k d , Bk |
vcosk d , |
2 |
||||
|
0 |
0 |
0 |
|
являющемся в ряде случаев более удобным при практическом вычислении коэффициентов.
Приближенный метод разложения. Часто периодическая функция,
подлежащая разложению в ряд Фурье, задается не аналитическим выражением, а в виде графика. В этих случаях прибегают к приближенным методам вычисления коэффициентов ряда. Один из наиболее распространенных методов этого рода заключается в замене интегралов, определяющих коэффициенты Ak и Bk ,
соответствующими конечными суммами (метод Перри).
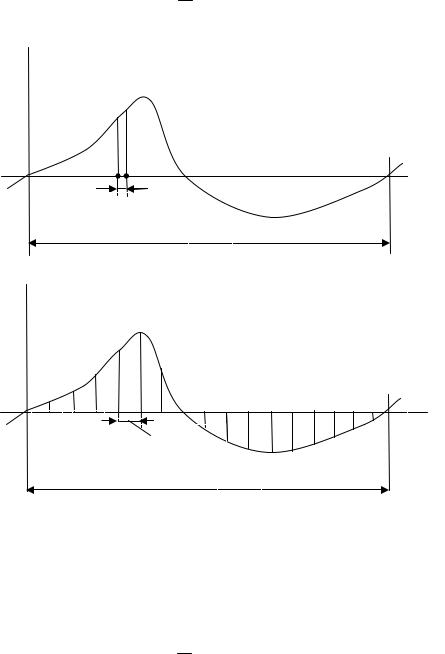
Представим разлагаемую кривую (рис. 1.1) как функцию угла , положив ее период равным 2 . Точное определение постоянной составляющей V0 предполагало бы вычисление интеграла
V0 21 20 v d ,
что соответствует суммированию в пределах всего периода бесконечно большого числа бесконечно малых слагаемых вида v d , каждое из которых представляет собой произведение ординаты v кривой в некоторой точке на бесконечно малое приращение аргумента d (рис. 1.1, а). Мы же, вместо деления периода на бесконечно большое число частей, осуществим его деление на ко-
нечное число p равных отрезков длиной |
2 / p (рис. 1.1, б) и перейдем к |
|||||||
приближенному вычислению коэффициента V0 , заменяя интегрирование сум- |
||||||||
мированием конечного числа слагаемых вида vi |
, собранных в пределах все- |
|||||||
го периода: |
|
|
|
|
|
|
||
|
1 2 |
1 |
p |
1 |
p |
2 |
||
V0 |
|
v d |
|
vi |
|
|
vi |
p |
2 |
2 |
2 |
||||||
0 |
|
1 |
|
|
1 |
|
||
или, вынося общие множители из-под знака суммы,
V0 1 p vi , p 1
где vi – ордината разлагаемой кривой в точках деления.
Таким образом, приближенное значение постоянной составляющей равно среднему арифметическому из ординат кривой в точках деления периода этой кривой на р равных частей.
Рассуждая аналогично, можно получить приближенное выражение и для коэффициентов Ak ряда Фурье:
|
1 |
2 |
1 |
p |
|
1 |
p |
2 |
Ak |
vsin k d |
vi sin k i |
|
vi sin k i |
||||
|
|
0 |
1 |
|
1 |
p |
||
или окончательно
Ak 2 p vi sin k i . p 1
a)v
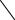 d
d
2
б) v
1 2 |
|
i |
d |
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
p |
2 |
|
|
|
|
|
Рис. 1.1. Разложение периодической несинусоидальной функции графическим методом
Соответствующее выражение для коэффициентов Bk будет выглядеть в
виде
Bk 2 p vi cos k i .
p 1
Иными словами, значения Ak и Bk равны удвоенным значениям средних арифметических произведений ординат vi во всех точках деления на значения sin k i и cosk i при соответствующих углах i .
Очевидно, что точность приближенных вычислений коэффициентов ряда Фурье будет тем выше, чем больше точек деления, и зависит от сложности разлагаемой кривой. При этом, как правило, вполне достаточная для инженерных расчетов точность достигается при делении периода на 15–20 частей.
О других методах разложения. Наряду с только что описанным, широко распространенным способом, существует множество других приемов приближенного разложения функций в ряд Фурье, построенных на основе аналитической, графоаналитической или чисто графической обработке заданной кривой.
В тех случаях, когда гармоническому анализу должны быть подвергнуты реальные напряжения и токи, кроме упомянутых косвенных методов, требующих наличия графиков этих величин, возможно применение гармонических анализаторов, в которые исследуемые напряжения и токи вводят непосредственно как физические величины. Следует подчеркнуть, что точность таких приборов часто намного превосходит точность косвенных методов.
Разложение функций, обладающих симметрией. Встречающиеся на практике переменные напряжения и токи в подавляющем большинстве случаев представляют собой периодические функции времени, отличающиеся той или иной симметрией, что приводит к заметному упрощению их разложения в ряд Фурье.
Рассмотрим три важных случая симметрии функции.
1) Наиболее часто мы встречаемся с кривыми напряжения и тока, симметричными относительно оси абсцисс, и обычно кратко называемых симметричными кривыми. Условие такой симметрии, математически выражающееся в виде f t f t 0,5T , заключается в том, что нижняя полуволна кривой, бу-
дучи смещенной вдоль оси абсцисс на полпериода, оказывается зеркальным отображением в этой оси верхней полуволны (рис. 1.2, а).
Не останавливаясь на доказательстве, обратим внимание на то, что в разложении таких кривых всегда отсутствуют постоянная составляющая и все четные гармоники (вторая, четвертая и т. д.).
Рис. 1.2. Разные виды симметрии функции
Иными словами, ряд Фурье, в который разлагается симметричная функция v f t , будет иметь вид
vk V1m sin t v1 V3m sin 3 t v3 V5m sin 5 t v5 ....
Очевидно, что при разложении такой функции нет необходимости обращаться к вычислению коэффициентов V0 , а также Ak и Bk с чётными индекса-
ми, так как они заведомо равны нулю.
2) Если функция симметрична относительно начала координат (рис. 1.2, б), то есть удовлетворяет условию f t f t , то в ее разложении будут от-
сутствовать постоянная составляющая V0 и все коэффициенты Bk при косину-
сах, то есть, как принято говорить, такая функция разлагается только по синусам:
vA1 sin t A2 sin 2 t ... Ak sin k t....
3)Если функция симметрична относительно оси ординат (рис. 1.2, в), то
есть удовлетворяет условию f t f t , то в ее разложении будут отсутствовать все коэффициенты Ak при синусах, то есть такая функция, в которой не исключено наличие постоянной составляющей V0 , изобразится рядом, состоящим из одних косинусов:
v V0 B1 cos t B2 cos 2 t ... Bk cos k t ...
В заключение заметим, что в практически встречающихся напряжениях и токах возможны совмещения первого случая симметрии со вторым или третьим случаем. Так, например, приведенная на рис. 1.2, г кривая, симметричная относительно оси абсцисс, является одновременно и симметричной относительно начала координат 0 или симметричной относительно оси ординат O v . При разложении такой кривой в ряд относительно начала O в нем будут присутствовать только синусы нечетных гармоник
vk A1 sin t A3 sin 3 t A5 sin 5 t ...,
а при разложении относительно начала O ряд будет содержать только косинусы нечетных гармоник
v B1 cos t B3 cos 3 t ... B5 cos 5 t ...
Разложение трапеции. Приведем в качестве примера разложение в ряд Фурье часто встречающейся в электротехнике симметричной функции v f t F t , графически изображающейся в виде равнобочной трапеции
(рис. 1.3, а) с высотой Vm и проекциями боковых сторон на ось абсцисс t , равными .
При выборе начала отсчета углов t в точке пересечения функции с
осью абсцисс, как показано на рис. 1.3, б, к условию симметрии этой функции относительно оси абсцисс добавляется условие симметрии относительно начала координат, то есть разложение будет содержать одни синусы нечетных гармоник и выглядеть в виде
|
4Vm |
1 |
|
1 |
|
||
v |
|
sin sin t |
|
sin 3 sin 3 t ... |
|
sin k sin k t ... . |
|
|
9 |
k 2 |
|||||
|
|
|
|
||||
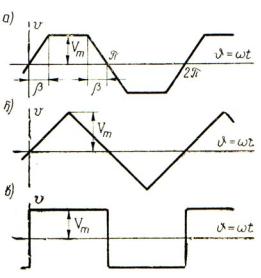
Характерным в разложении является присутствие в амплитудах гармоник множителя 1/ k 2 , свидетельствующего об их быстром уменьшении по мере возрастания номера гармоники. Из приведенного ряда следует также, что амплитуды гармоник зависят от формы трапеции (множителя sin k ).
Рис. 1.3. Трапецеидальная форма периодической кривой
В частном случае 0,5 (пилообразная функция, рис. 1.3, б) имеет
вид |
|
|
|
|
|
|
|
|
|
|
|
8V |
|
|
1 |
|
|
|
1 |
|
|
v |
m sin t |
|
sin 3 t |
|
|
sin 5 t ... . |
||||
9 |
25 |
|||||||||
|
2 |
|
|
|
|
|||||
При 0 (прямоугольная функция, рис. 1.3, в) разложение приобретает |
||||||||||
вид |
|
|
|
|
|
|
|
|
|
|
|
4V |
m |
|
1 |
|
|
1 |
|
||
v |
|
sin t |
|
|
sin 3 t |
|
sin 5 t ... . |
|||
|
3 |
5 |
||||||||
|
|
|
|
|
||||||
Влияние высших гармоник на форму кривой периодической функции.
На практике нередко встречаются случаи, когда на синусоидально изменяющиеся ток и напряжение по тем или иным причинам накладывается всего одна какая-либо высшая гармоника. При этом наблюдается сильное искажение результирующей кривой по сравнению с синусоидальной функцией. На рис. 1.4 в качестве примеров приведены формы кривых результирующих функций (показаны только положительные полуволны) при наложении на синусоиду третьей (рис. 1.4, а) и пятой (рис. 1.4, б) гармоник, составляющих по величине четвер-
тую часть от основной волны, но по-разному сдвинутых по фазе относительно первой гармоники.
Кривые на рис. 1.4, а отвечают уравнению
vsin t 14 sin 3 t 3 ,
акривые на рис. 1.4, б соответствуют выражению
vsin t 14 sin 5 t 5 .
Из рисунка следует, что на форму кривой результирующей функции сильно влияет не только порядок гармоники, но и ее расположение по фазе относительно основной волны.
Ряды ЭДС, напряжения и тока. В качестве примеров приводим общие случаи записи разложения несинусоидальных ЭДС, напряжения и тока в гармонические ряды:
e E0 E1m sin t e1 E2m sin 2 t e2 ... Ekm sin(k t ek ) ..., u U0 U1m sin t u1 U2m sin 2 t u2 ... Ukm sin(k t uk ) ..., i I0 I1m sin t i1 I2m sin 2 t i2 ... Ikm sin(k t ik ) ... .
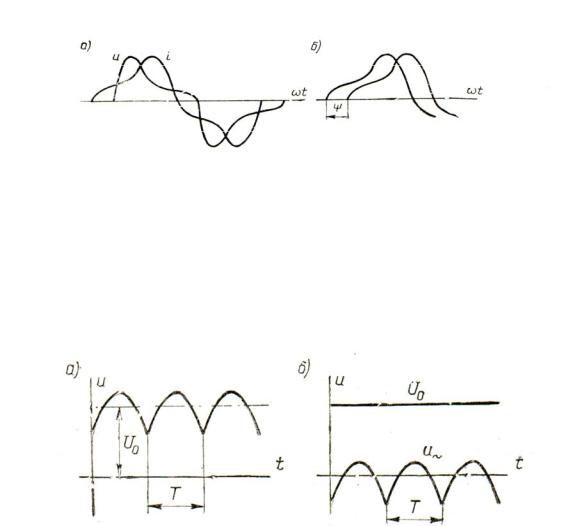
О сдвиге несинусоидальных функций во времени. При сопоставлении двух синусоидальных функций времени мы широко пользовались понятием разности фаз, в частности разности фаз напряжения и тока. Обратим внимание, что аналогичного понятия для несинусоидальных функций ввести в общем случае, когда две функции выражаются разными законами, не представляется возможным. Наиболее ярко это можно продемонстрировать на примере несинусоидальных кривых напряжения и тока, представленных на рис. 1.5, а. Здесь невозможно определить не только числовые значения угла сдвига этих кривых, но даже и его знак: если судить по точкам пересечения этих кривых с осью абсцисс, то опережающей кажется кривая тока i ; если же ориентироваться по положениям максимумов рассматриваемых кривых, то опережающей следует признать кривую напряжения u .
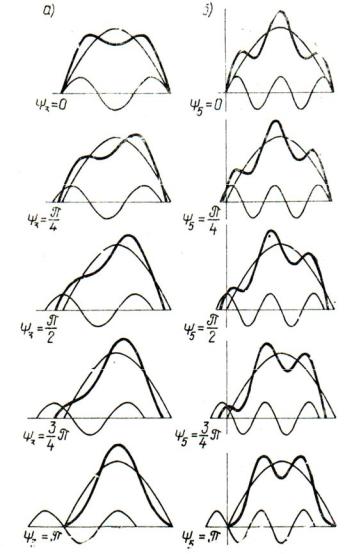
Рис. 1.4. Наиболее распространенные в электротехнике формы кривых периодических функций
Лишь в частном случае точного совпадения законов изменения двух величин во времени (рис. 1.5, б) возможно употребление понятия угла сдвига между этими величинами.
О векторных диаграммах и символическом методе при несину-
соидальных токах и напряжениях. Следует особо подчеркнуть, что при несинусоидальных токах и напряжениях нельзя прибегать к векторным диаграммам, так как с помощью векторов можно изображать только синусоидально меняющиеся величины. Соответственно этому при несинусоидальных токах и напряжениях неприменим и символический метод расчета электрических цепей, поскольку он является логическим продолжением метода векторных диаграмм.
Ри
с. 1.5. Виды несинусоидальных периодических функций
Пульсирующие напряжения и токи. В некоторых областях электро-
техники мы встречаемся с пульсирующими напряжениями и токами, которые, не меняясь по направлению, периодически колеблются по величине (рис. 1.6,а). Поскольку в подобных случаях практический интерес
Рис. 1.6. Пульсирующие периодические напряжения
в основном представляет среднее значение величины, то ее мгновенное значение принято оценивать суммой только двух слагаемых. Например, напряжение u можно представить суммой постоянной составляющей U0 , равной среднему
значению, и переменной составляющей u~
u U0 u~
(см. также рис. 1.6, б), часто не раскрывая гармонический состав второго слагаемого.
Период T пульсирующих величин (рис. 1.6), равный периоду их переменной составляющей, обычно называют периодом пульсаций.
1.3. Характеристики несинусоидальных токов

Действующее значение несинусоидального тока определяется общим выражением:
|
|
1 |
T |
|
I |
i2 d t , |
|||
T |
||||
|
0 |
|||
|
|
|
||
справедливым при любом периодическом законе изменения переменного тока. Представляя мгновенное значение i несинусоидального тока как сумму
мгновенных значений гармоник (включая и постоянную составляющую)
i i0 |
i1 i2 |
i3 |
... ik |
... ik , |
|
|
|
|
k |
для квадрата тока путем почленного перемножения двух одинаковых рядов получим
i2 ik2 2iqis ,
k q,s
где первое слагаемое представляет собой сумму квадратов мгновенных значений токов всех гармоник, а второе слагаемое объединяет собой удвоенные произведения двух токов с различными индексами в различных комбинациях
( q s ).
Тогда для квадрата действующего значения тока имеем
|
|
1 |
T |
|
1 |
T |
|
1 |
T |
|
I 2 |
|
i2 d t |
ik2d t |
2iqis d t . |
||||||
T |
T |
T |
||||||||
|
|
|
0 |
k |
0 |
q,s |
0 |
|||
Рассмотрим определенный интеграл:
T |
T |
q t q sin s t s d t , |
2iqis d t Iqm Ism 2sin |
||
0 |
0 |
|
памятуя, что q и s - целые положительные числа.
Преобразуя в подынтегральном выражении произведение синусов в разность косинусов по известной формуле тригонометрии
sin xsin y 0,5 cos x y cos x y ,
для рассматриваемого интеграла получим
T |
T |
T |
2iqis d t Iqm Ism{ cos q s t q s d t cos q s t q s d t}. |
||
0 |
0 |
0 |
При q s |
оба интеграла, представленные в правой части равенства, рав- |
|
ны нулю как интегралы синусоидальных функций, взятые за целое число периодов. Отсюда будет равен нулю и рассматриваемый интеграл:
T
2iqis d t 0,
0
то есть квадрат действующего значения тока запишется короче:
|
|
1 |
T |
|
1 |
T |
|
I 2 |
|
i2 d t |
ik2d t . |
||||
T |
T |
||||||
|
|
|
0 |
k |
0 |
||
В выражении под знаком суммы нетрудно узнать квадрат действующего значения тока k -й гармоники, а потому
I 2 Ik2
k
или
I |
Ik2 |
|
I02 I12 I22 ... Ik2 ... , |
(1.5) |
|
k |
|
|
|
то есть действующее значение несинусоидального тока равно корню квадратному из суммы квадратов действующих значений гармоник. При этом постоянная составляющая рассматривается как частный случай гармоники с угловой частотой, равной нулю (нулевая гармоника).
Аналогично определяются действующие значения несинусоидальных напряжений и ЭДС.
U |
Uk2 |
U02 U12 |
U22 |
... Uk2 |
... , |
(1.6) |
|
k |
|
|
|
|
|
E |
Ek2 |
E02 E12 |
E22 |
... Ek2 |
... . |
(1.7) |
|
k |
|
|
|
|
|
Следует иметь в виду, что в формировании действующего значения несинусоидальной величины высшие гармоники, как правило, играют второстепенную роль. Например, высшая гармоника, составляющая по величине пятую часть от основной волны (20 %), увеличивает действующее значение результирующей величины всего на 2 % по сравнению с действующим значением первой гармоники:
V V 2 |
V 2 |
|
12 (0,2)2 |
|
1,04 1,02 . |
1 |
5 |
|
|
|
|
Обращаем внимание также на то, что действующее значение несинусоидальной функции определяется только величиной гармоник и не зависит от их фазы, в то время как форма кривой претерпевает резкие изменения с изменением фазы гармоник.

Активная мощность цепи при наличии высших гармоник в токе и напряжении определяется по общему правилу как среднее значение мгновенной мощности за период
|
|
1 |
T |
1 |
T |
|
P |
p d t |
ui d t . |
||||
T |
T |
|||||
|
0 |
0 |
||||
|
|
|
|
|||
Представляя напряжение и ток в виде рядов u u0 u1 u2 ... uk ...,
i i0 i1 i2 ... ik ...
и перемножая их, мгновенную мощность цепи представим в виде двух сумм: p ui uk ik uqis ,
kq,s
впервую из которых входят произведения напряжения и тока одинаковых гармоник, а во вторую - собраны все произведения с разными индексами у напряжения и тока ( q s ).
Подставляя полученное выражение под интеграл, для активной мощности получим
|
1 |
T |
|
1 |
T |
|
P |
uk ik d t |
uqis d t |
||||
T |
T |
|||||
k |
0 |
q,s |
0 |
|||
или
P 1 T uk ik d t ,
k T 0
так как при q s второй интеграл обращается в нуль, что нетрудно доказать
приемом, приведенным для аналогичного случая в предыдущем пункте. Под знаком же суммы в последнем выражении легко усмотреть активную мощность k-й гармоники. Следовательно, активная мощность цепи при несинусоидальных токах и напряжениях определяется суммой активных мощностей отдельных гармоник:
|
P Pk P0 P1 P2 ... Pk .... |
(1.8) |
|
k |
|
Выражая здесь отдельные слагаемые по известным формулам мощности |
||
при постоянных и синусоидальных токах и напряжениях, получим |
|
|
|
P U0 I0 U1I1 cos 1 U2 I2 cos 2 ... Uk Ik cos k ..., |
(1.9) |
где k |
uk ik – разность фаз напряжения и тока k -й гармоники. |
|
Полная мощность цепи при несинусоидальных напряжениях и токах определяется через их действующие значения U и I тем же выражением
S UI ,
что и при синусоидальных величинах. При этом подчеркиваем, что в общем случае полная мощность цепи при наличии высших гармоник напряжения и тока не может быть выражена простым путем через полные мощности отдельных гармоник.
Реактивная мощность. К реактивной мощности цепи при несинусоидальных напряжениях и токах обращаются сравнительно редко, определяя ее
формально как сумму реактивных мощностей отдельных гармоник: |
|
|
Q Qk Q1 Q2 |
... Qk ... |
(1.10) |
k |
|
|
или в развернутом виде
Q U1I1 sin 1 U 2 I 2 sin 2 ... U k I k sin k .... (1.11)
При этом понятия реактивной мощности постоянной составляющей, естественно, не существует.
О соотношении между мощностями. При несинусоидальных токах и напряжениях нарушается привычная связь между полной, активной и реактивной мощностями цепи, и даже при отсутствии постоянных составляющих в напряжении и токе имеет место неравенство
S P2 Q2 .
Поэтому при несинусоидальных напряжениях и токах иногда наряду с реактивной мощностью, вводят понятие о мощности искажения Т, определяемой из соотношения
S P 2 Q 2 T 2 .
Коэффициент мощности при несинусоидальных напряжениях и токах обозначают греческой буквой («хи») и определяют отношением активной мощности цепи к ее полной мощности:
|
P . |
(1.12) |
|
S |
|
Обозначение коэффициента мощности цепи при несинусоидальных напряжениях и токах в виде cos не употребляется, поскольку разность фаз в
этих условиях не имеет смысла.
Как и при синусоидальных напряжениях, коэффициент мощности чисто активной цепи, то есть цепи, не содержащей катушек и конденсаторов, при ус-

ловии ее линейности равен единице. В остальных случаях он оказывается меньше единицы.
Критерии формы кривых. Для оценки формы кривых несинусоидальных токов и напряжений в электротехнике пользуются рядом коэффициентов. Ниже приведены понятия о наиболее важных из этих коэффициентов, которые используются, правда, для оценки формы кривой только при отсутствии в них постоянной составляющей.
Коэффициент амплитуды представляет собой отношение максимального значения Vm данной величины к ее действующему значению V:
ka Vm /V . |
(1.13) |
Как следует из ранее изученного материала, коэффициент амплитуды для
синусоиды равен  2 . Для величин с прямоугольной формой волны (см. рис. 1.3, в), когда понятия максимального Vm , действующего V, а кстати, и среднего
2 . Для величин с прямоугольной формой волны (см. рис. 1.3, в), когда понятия максимального Vm , действующего V, а кстати, и среднего
VCP значения совпадают, коэффициент амплитуды равен единице. При пилообразном законе изменения величины (см. рис. 1.3, б) коэффициент амплитуды принимает значение  3 .
3 .
В общем случае коэффициент амплитуды может принимать любые значения больше единицы, причем он становится тем больше, чем острее форма кривой данной величины.
Коэффициент амплитуды обычно используют для выражения максимального значения величины через ее действующее значение или, наоборот, действующего значения через максимальное.
Коэффициент формы устанавливает связь между действующим V и
средним VCP значениями данной величины |
|
kф V /VCP |
(1.14) |
и широко используется для вычисления одной из упомянутых величин через другую.
Обращаясь к ранее полученным связям между средним, действующим и максимальным значениями синусоидальной функции
V |
|
2 |
V |
|
, |
V Vm |
, |
|
|
||||||
CP |
|
|
m |
|
2 |
|
|
нетрудно определить коэффициент формы для синусоиды:
kФ |
V |
|
1 |
: |
2 |
|
|
|
1,11. |
|
VCP |
2 |
|
2 |
2 |
||||||
|
|
|
|
|

Для функции с прямоугольной формой волны, когда V VCP , коэффици-
ент формы равен единице. В общем случае коэффициент формы, оставаясь большим единицы, принимает тем большее значение, чем острее форма кривой тока.
Коэффициент гармоник служит для оценки относительного содержания высших гармоник в несинусоидальной функции по сравнению с основной волной и определяется отношением действующего значения всех высших гармоник вместе взятых к действующему значению первой гармоники
|
|
V 2 |
V 2 |
|
|
кГ |
|
|
1 |
. |
(1.15) |
|
|
||||
|
|
V1 |
|
||
Соответствие числителя в этом выражении приведенному выше определению становится очевидным, если вспомнить полученную ранее формулу для действующего значения V несинусоидальной функции (при отсутствии постоянной составляющей):
V 2 V12 V22 V32 ... Vk2 ....
Из этой формулы следует, что разность V 2 V12 определяет собой сумму
квадратов действующих значений всех высших гармоник, то есть квадрат действующего значения всех гармоник выше первой.
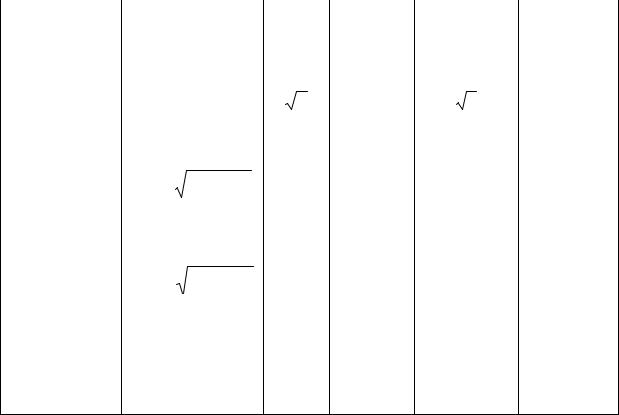
Коэффициент гармоник для синусоиды, естественно, равен нулю (синусоида при разложении в ряд Фурье дает самое себя без каких-либо гармоник). Из табл. 1.1, где приведены значения коэффициента гармоник для волны прямоугольной и треугольной форм, следует, что содержание высших гармоник в первом случае ( kГ 0,483) значительно больше, чем вo втором ( k Г 0,122 ).
Заметим, что на практике коэффициент гармоник часто выражают в процентах, увеличивая результат вычисления по формуле (1.15) в 100 раз.
Коэффициент искажения также оценивает содержание высших гармоник в разложении данной величины в ряд Фурье и отличается от коэффициента гармоник только тем, что оценка эта делается не по отношению к первой гармонике, а по отношению к действующему значению V всей величины в целом:
|
V 2 |
V 2 |
|
|
кИ |
|
1 |
. |
(1.16) |
|
|
|||
|
V |
|
||
При незначительном отклонении формы кривой от синусоиды различие в числовых значениях коэффициента искажения и коэффициента гармоник едва заметное (см. табл. 1.1), и поэтому практически не возникает необходимости
одновременно пользоваться этими коэффициентами. В сильноточной электротехнике чаще оперируют коэффициентом гармоник, а в радиотехнике предпочитают пользоваться коэффициентом искажения.
Коэффициент синусоидальности оценивает степень приближения формы кривой к синусоиде и определяется отношением действующего значения V1
первой гармоники разложения к действующему значению V всей величины в целом:
V1 /V . |
(1.17) |
Для синусоиды, когда V1 V , этот коэффициент принимает наибольшее
значение, равное единице, а при искаженных формах кривых он становится меньше единицы (см. табл. 1.1).
Коэффициент синусоидальности широко используется в энергетике при вычислении мощности в нелинейных цепях переменного тока.
Заметим, что в русском техническом языке коэффициент синусоидальности часто неудачно называется коэффициентом искажения. Во-первых, это название не соответствует смысловому содержанию этого коэффициента, так как по величине он становится тем меньше, чем больше искажения формы кривой. Во-вторых, при употреблении этого термина, занятого в радиотехнике другим понятием (см. коэффициент искажения), возможны недоразумения при оценке степени искажения кривых.
Примеры числовых значений коэффициентов, характеризующих форму кривой, приведены в табл. 1.1 для синусоиды кривой с прямоугольной формой волны и пилообразной функции.
Практически синусоидальные кривые. Хотя при конструировании гене-
раторов переменного тока и стремятся к получению от них синусоидальных напряжений, добиться этого в полной мере не удается. Поэтому на практике мы встречаемся с напряжениями, а следовательно, и токами, форма которых лишь в той или иной степени приближается к синусоидальной. Если отклонения действительных кривых напряжения или тока от строгой синусоиды незначительны, то говорят о практически синусоидальных величинах.
|
|
|
|
|
Таблица 1.1 |
|
|
Коэффициенты, характеризующие формы кривых |
|||||
|
|
|
|
|
|
|
Наименова- |
Обозначение и |
Числовые значения |
Область |
|
||
ния коэффи- |
коэффициентов |
|
||||
циентов |
определение |
|
|
|
значений |
|
|
Сину- |
Прямо- |
Треуголь- |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
соида |
уголь- |
ная форма |
|
|
|
|
|
|
|
|
|
|
|
ная |
|
|
|
|
|
|
|
|
|
|
|
|
форма |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Амплитуды |
ka Vm / V |
|
2 |
1 |
3 |
ka 1 |
||||||
Формы |
kф V / VCP |
|
1,11 |
1 |
1,15 |
kФ 1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V 2 V |
2 |
|
|
|
|
|
|
|
Гармоники |
кГ |
|
1 |
0 |
0,483 |
0,122 |
0 кГ |
|
||||
|
V1 |
|
||||||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V 2 V 2 |
|
|
|
|
|
|
|
|
Искажения |
кИ |
|
|
|
1 |
|
0 |
0,435 |
0,120 |
0 к |
|
1 |
|
V |
|
|
И |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Синусои- |
|
|
|
V1 /V |
1 |
0,90 |
0,99 |
0 1 |
||||
дальности |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Согласно ГОСТу практически синусоидальным напряжением называется такое напряжение, у которого коэффициент гармоник, то есть отношение действующего значения всех высших гармоник к действующему значению основной волны, не превышает 5 % ( кГ 0,05 ). Однозначного определения практи-
чески синусоидального тока пока нет.
1.4. Расчет цепей при несинусоидальных токах
Этапы расчета. Выше подчеркивалось, что в линейных электрических цепях несинусоидальные токи могут возникнуть только под действием источников с несинусоидальными ЭДС. Поэтому наиболее естественной постановкой задачи о расчете таких цепей является определение токов в этих цепях по заданным ЭДС источников. Однако в ряде практических задач, относящихся к расчету отдельных участков цепи, заданной величиной может оказаться как несинусоидальное напряжение, так и несинусоидальный ток.
Вне зависимости от постановки задачи ее решение в соответствии с основной идеей расчета линейных цепей при синусоидальных токах будет состоять из трех этапов:
1) разложение заданной несинусоидальной величины, характеризующей режим работы цепи (ЭДС, напряжения или тока), на гармонические составляющие;

2)расчет цепи для каждой из гармоник в отдельности;
3)определение интегральных характеристик режима цепи (действующих значений токов и напряжений, мощности и коэффициента мощности в отдельных ветвях и всей цепи в целом).
Ограничиваясь приведенными выше замечаниями по первому этапу, представляющему собой скорее математическую, чем электротехническую задачу, остановимся подробнее на двух последующих этапах. При этом в первую очередь обратим внимание на зависимость параметров цепи от номера гармоники заданной несинусоидальной величины.
Сопротивления и проводимости гармоник. Параметры элементов элек-
трических цепей переменного тока в общем случае зависят от частоты. В частности, зависят от нее сопротивления и проводимости этих элементов, приобретающие вследствие этого при каждой гармонике свое особое значение. Различают их в названиях и обозначениях по номерам гармоник, например полное сопротивление первой гармоники ( z1 ), активное сопротивление третьей гармо-
ники ( r1), комплексная проводимость пятой гармоники (Y5 ) и т. д.
Естественно, что все известные соотношения между сопротивлениями и проводимостями сохраняются лишь в пределах данной k -й гармоники. В частности, имеем
z |
k |
r2 |
x2 |
, |
y |
k |
|
g 2 |
b2 |
, |
|
k |
k |
|
|
|
k |
k |
|
||
|
Zk rk jxk , |
Yk gk jbk . |
|
|||||||
Сопротивления и проводимости идеальных элементов. Поскольку ин-
дуктивное сопротивление идеальной катушки с индуктивностью L пропорционально частоте, оно для k -й гармоники определяется произведением
xLk |
k L , |
(1.18) |
||
где – угловая частота основной волны. |
|
|||
Емкостное сопротивление идеального конденсатора с емкостью С, обрат- |
||||
но пропорциональное частоте, выразится для k -й гармоники в виде |
|
|||
x |
|
1 |
. |
(1.19) |
|
||||
Ck |
|
k C |
|
|
|
|
|
||
Активное сопротивление идеального резистора не зависит от частоты и всегда равно его электрическому сопротивлению R:
rk R . |
(1.20) |
Для полного сопротивления k -й гармоники идеальной последовательной цепи RLC (рис. 1.7, а) получим
|
|
2 |
|
1 |
2 |
|
|
zk |
R |
|
k L |
|
|
. |
(1.21) |
|
|
||||||
|
|
|
|
k C |
|
|
|
а) |
|
|
|
|
|
б) |
|
R |
L |
G |
L |
|
|
C |
C |
||
|
|
|
Рис. 1.7. Электрические цепи с идеальными элементами Проводимости k-й гармоники идеальных катушки, конденсатора и рези-
стора соответственно представятся в виде |
|
|
|
|
|||||
b |
Lk |
|
1 |
, |
b |
k C , |
g |
k |
G , |
|
|||||||||
|
|
k L |
|
Ck |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
и поэтому для полной проводимости k -й гармоники идеальной параллельной цепи GLC (рис. 1.7, 6) будем иметь
|
|
2 |
|
1 |
|
2 |
yk |
G |
|
|
|
k C . |
|
|
|
|||||
|
|
|
k L |
|
|
|
По приведенным формулам можно вычислять сопротивления и проводимости идеальных элементов и для постоянной составляющей тока, если условно принять постоянную составляющую за гармонику нулевого порядка ( k 0), что соответствует приравниванию постоянного тока переменному с бесконечно малой частотой его изменения. При этом получим
xL0 0, xC0 , r0 R , bL0 ,bC0 0, g0 G .
Параметры реальных элементов. В действительности, зависимость параметров элементов цепи переменного тока от номера гармоники выглядит значительно сложнее приведенных выше формул, и поэтому расчет по ним является в той или иной мере приближенным. Это объясняется тем, что с повышением номера гармоники, то есть с увеличением частоты тока, наблюдается более яркое проявление многих сложных электромагнитных явлений в электрических
устройствах, которые не были учтены при установлении упомянутых простых зависимостей. И если при основной частоте пренебрежение этими явлениями было вполне допустимо, то на высших гармониках, то есть при повышенных частотах, такое пренебрежение может повлечь заметные погрешности в расчете.
Впервую очередь это относится к активному сопротивлению цепи, которое лишь до определенных границ можно считать независимым от номера гармоники. С повышением номера, а следовательно, и частоты гармоники начинает более ярко проявляться поверхностный эффект, приводящий к увеличению активного сопротивления проводов. Кроме того, с повышением частоты наблюдается усиление вихревых токов, индуктирующихся в конструктивных элементах устройств, также влекущее за собой увеличение активного сопротивления электрических контуров. К этому же результату ведет возрастание с частотой и потерь энергии в конденсаторах, и потерь энергии в магнитопроводах индуктивных катушек. Одним словом, активное сопротивление реальных устройств цепи переменного тока увеличивается по мере возрастания номера гармоники, причем это увеличение, весьма трудно оцениваемое расчетным путем,
вотдельных случаях при высоких гармониках может играть существенную роль.
Изменяются с частотой, то есть с порядком гармоники, и эквивалентные индуктивности реальных катушек и обмоток. Кроме того, на эти индуктивности оказывают влияние поверхностный эффект и вихревые токи, по мере увеличения номера гармоники все сильнее сказывается емкость между витками катушек, которая вызывает уменьшение их эквивалентной индуктивности.
Вконденсаторах при больших частотах, то есть на высоких гармониках, иногда приходится считаться с изменением их эквивалентной емкости за счет индуктивности подводящих проводов, и даже самих обкладок конденсаторов.
Расчет простых цепей переменного тока для каждой гармоники заданного напряжения или тока ничем не отличается от аналогичных задач, рассмотренных ранее, и может быть выполнен как с применением символического метода, так и без его помощи. В общих случаях в основе расчета лежит закон Ома, которым в зависимости от поставленной задачи можно связать или амплитуды тока или напряжения
Ukm Zk Ikm , |
Ukm zk Ikm , |
или их действующие значения
Uk Zk Ik , |
Uk zk Ik . |
В первом случае по окончании расчета цепи при всех выбранных гармониках необходимо по полученным максимальным значениям токов и напряжений отдельных гармоник определить их действующие значения, необходимые для вычисления интегральных значений искомых несинусоидальных величин. Во втором случае расчет начинают с вычисления действующих значений гармоник заданной несинусоидальной величины, ориентируясь на коэффициенты ее разложения в гармонический ряд.
При необходимости записать ряды искомых несинусоидальных величин наряду с максимальными значениями гармоник необходимо определить начальные фазы гармоник этих величин. В этом случае особенно удобным является символический метод расчета, так как при соответствующей записи комплексных амплитуд гармоник заданной величины (с учетом их начальных фаз) каждая из полученных в результате расчета величин будет нести в себе информацию и о начальной фазе.
Активная мощность цепи или ее отдельных элементов рассчитывается как сумма мощностей отдельных гармоник, причем для каждой составляющей остаются справедливыми известные выражения:
Pk Uk Ik cos k rk Ik2 gkUk2 .
Полная мощность находится по действующим значениям соответствующих напряжения и тока:
SUI ,
адля определения коэффициента мощности используется формула
PS .
Расчет сложных цепей при несинусоидальных ЭДС источников и приложенных к цепи напряжений включает в себя те же три ранее упомянутых этапа и отличается от аналогичной задачи для простых цепей только техникой выполнения второго этапа, то есть приемами расчета цепи при заданных синусоидальных величинах отдельных гармоник. Все расчеты второго этапа проводят символическим методом.
1.5. Метод эквивалентных синусоид
Идея метода. В ряде случаев приближенных расчетов цепей с несинусоидальными токами и напряжениями в целях упрощения задачи прибегают к

методу эквивалентных синусоид, заключающемуся в том, что вместо заданных несинусоидальных величин вводят эквивалентные синусоиды, под которыми понимают синусоидально изменяющиеся величины с действующим значением, равным действующему значению данных несинусоидальных функций. Весь дальнейший расчет проводится обычным методом расчета цепи при синусоидальных токах и напряжениях.
Приближенное определение эквивалентной синусоиды. Вычисление действующего значения заданной несинусоидальной функции можно выполнить, не разлагая эту функцию в гармонический ряд, а пользуясь общим выражением для действующего значения периодической функции:
|
|
1 |
T |
|
V |
v2 d t . |
|||
T |
||||
|
0 |
|||
|
|
|
||
Если функция v f t задана графически, с чем мы чаще всего встреча-
емся в электротехнической практике, то вычисления ведут приближенным методом, переходя от интеграла к конечной сумме. Для этого период исследуемой функции делят на конечное число n равных частей (рис. 1.8) продолжительно-
стью t T / n , определяют ординаты vi |
кривой во всех точках деления и, об- |
||||||
ращаясь к приближенному равенству |
|
|
|
|
|
||
|
|
|
|
|
|
i n |
|
|
1 i n |
|
|
t i n |
vi2 |
|
|
V |
|
vi2 |
t |
|
vi2 |
i 1 |
, |
|
T |
n |
|||||
|
T i 1 |
|
i 1 |
|
|||
вычисляют действующее значение по последнему выражению:
i n
vi2
V |
i 1 |
. |
(1.22) |
|
|||
|
n |
|
|
Максимальное значение эквивалентной синусоиды будет в  2 раз больше полученного действующего значения.
2 раз больше полученного действующего значения.
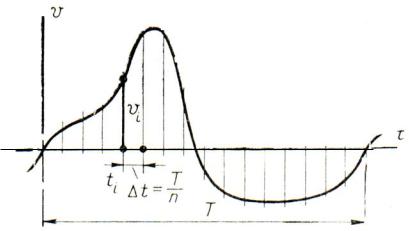
Рис. 1.8. Исследуемая периодическая несинусоидальная функция
Точность результата в общем случае будет тем выше, чем больше точек деления, при выборе числа которых приходится ориентироваться также на сложность периодической функции. Как правило, деление периода на 15–20 частей удовлетворяет требованиям точности инженерного расчета.
Векторное изображение эквивалентных синусоид. Оперирование экви-
валентными синусоидами взамен действительных несинусоидальных величин возвращает нас к возможности их векторного изображения, то есть к иллюстрации режима работы цепей даже с несинусоидальными токами и напряжениями с помощью векторных диаграмм. Этим широко пользуются на практике, часто не оговаривая факт построения диаграммы именно для эквивалентных синусоид.
Разность фаз эквивалентных синусоид напряжения и тока. В тех слу-
чаях, когда на диаграмме должны фигурировать векторы, изображающие эквивалентные синусоиды напряжения и тока, возникает вопрос об угле сдвига между этими векторами, то есть, иначе говоря, о разности фаз эквивалентных синусоид напряжения и тока. С целью наиболее полного отражения эквивалентными синусоидами энергетического режима исследуемой цепи их принято сдвигать друг относительно друга на угол , определяемый из соотношения
P UI cos ,
где P – активная мощность цепи при несинусоидальных токах и напряжениях. Таким образом, эквивалентные синусоиды напряжения и тока, а следовательно, и их векторы сдвигают друг относительно друга на угол, обеспечивающий при приближенных расчетах по эквивалентным синусоидам действитель-
ную мощность цепи.
1.6. Воздействие линейной цепи на гармоники тока
Влияние характера цепи на форму кривой тока. Как показывает опыт,
при питании электрической цепи несинусоидальным напряжением форма кривой тока в ней в общем случае отличается от формы кривой напряжения, то есть цепь оказывает определенное влияние на форму кривой тока при заданной форме кривой питающего напряжения. Остановимся на этом вопросе подробнее, рассмотрев несколько простейших примеров.
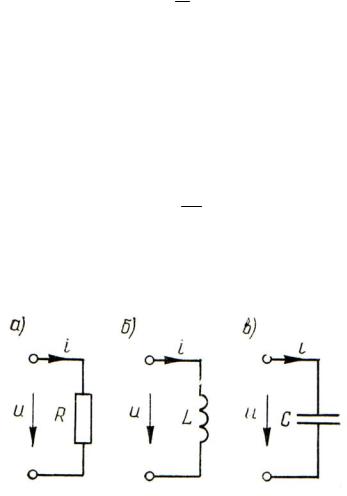
а) В частном случае цепи, состоящей из идеального резистора с сопротивлением R (рис. 1.9, а), форма кривой тока в точности совпадает с формой кривой напряжения, что непосредственно вытекает из пропорциональности мгновенного значения тока в такой цепи мгновенному значению приложенного к ней напряжения:
i Ru .
Это обстоятельство часто используется в измерительной технике, когда взамен технически более сложной задачи и осциллографирования кривой тока обращаются к более легкой задаче снятия кривой напряжения на резисторе, по которому протекает исследуемый ток.
б) В цепи с идеальной катушкой (рис. 1.9, б) напряжение и ток связаны дифференциальной зависимостью
u L dd ti ,
и поэтому, за исключением случая чисто синусоидальных величин, кривые напряжения и тока будут различаться по форме.
Рис. 1.9. Простые электрические цепи с идеальными элементами

Нетрудно убедиться, что такая цепь будет приводить к уменьшению содержания высших гармоник в кривой тока по сравнению с их содержанием в кривой питающего напряжения. Действительно, чем выше номер гармоники, иначе говоря, ее частота, тем больше индуктивное сопротивление катушки для этой гармоники, и следовательно, тем меньше будет проявлена эта гармоника в кривой тока. Иными словами, форма кривой тока в катушке будет ближе к синусоиде, чем форма кривой напряжения.
Строго это можно показать, сравнив ток и напряжение в простейшей индуктивной цепи по коэффициенту гармоник, полагая для простоты, что напряжение, кроме основной волны, содержит только одну высшую гармонику. При этом коэффициент гармоник напряжения выразится в виде
kГu Uk , U1
где Uk и U1 - действующие напряжения k -й гармоники и основной волны.
Токи k –й гармоники и основной волны определятся соответственно выражениями
Ik Uk |
Uk |
|
Uk |
и I1 |
U1 |
U1 |
U1 |
, |
|
k L |
|||||||||
zk |
xLk |
|
|
z1 |
xL1 |
L |
|
откуда для коэффициента гармоник тока получим
kГi |
Ik |
|
Uk |
kГu , |
|
I1 |
kU1 |
||||
|
|
k |
то есть он будет в k раз меньше, чем коэффициент гармоник напряжения, что и свидетельствует о меньшем искажении кривой тока по сравнению с кривой напряжения.
Обобщая рассмотренный пример, можно прийти к выводу о том, что всякая индуктивная цепь сглаживает форму кривой тока по сравнению с кривой питающего напряжения.
в) В идеальном конденсаторе ток и напряжение связаны интегральной зависимостью
u iCd t ,
и они при несинусоидальном законе изменения также будут отличаться друг от друга по форме. Однако в этом случае ток конденсатора окажется более искаженным, чем приложенное к нему напряжение, так как емкостное сопротивление конденсатора падает с повышением частоты и, следовательно, с увеличени-
ем номера гармоники. Поэтому гармоники высших порядков будут проявлены в токе относительно более ярко, чем в приложенном к конденсатору напряжении.
Для строгого доказательства этого положения обратимся к примеру, когда на конденсаторе (рис. 1.9, в), как и в предыдущем случае, действует напряжение, содержащее, кроме основной волны, одну высшую, например k-ю гармонику. Токи этой гармоники и основной волны определяются выражениями
I |
k |
Uk Uk |
U |
k |
k C и I |
1 |
U1 |
|
U1 |
U C , |
|
|
|||||||||||
|
zk |
xCk |
|
|
z1 |
|
1 |
||||
|
|
|
|
|
|
|
xC1 |
||||
где Uk и U1 - действующие напряжения k-й гармоники и основной волны. Отсюда для коэффициента гармоник тока получим
kГi |
Ik |
Uk k kГu k , |
|
I1 |
|||
|
U1 |
то есть он будет в k раз больше коэффициента гармоник приложенного напряжения, что и свидетельствует о большем искажении кривой тока по сравнению с кривой напряжения.
Обобщая полученный результат, можно сказать, что емкостная цепь усиливает искажение кривой тока по сравнению с кривой приложенного к цепи напряжения.
Понятия о частотных фильтрах. Зависимость формы кривой тока в электрической цепи при ее питании несинусоидальным напряжением от содержащихся в цепи элементов и схемы их соединения широко используется на практике для преднамеренного управления гармоническим составом тока, или напряжением, приемников. С этой целью между источником и приемником включают промежуточное устройство, представляющее собой четырехполюсник со специально подобранными схемами и называемыми частотными электрическими фильтрами. Обладая определенными частотными характеристиками, такие фильтры осуществляют подавление или, наоборот, усиление отдельных гармоник тока и напряжения, а также распределение их по различным участкам цепи.
Наиболее типичными задачами, решающимися с помощью фильтров в области сильноточной электротехники, являются или улучшение формы кривой тока и напряжения, то есть возможное приближение ее к синусоидальной форме, или сглаживание пульсирующих токов и напряжений, заключающееся в подавлении их переменных составляющих.
Ниже приведены несколько примеров прозрачных и заграждающих фильтров, первые из которых служат для выделения той или иной гармоники из несинусоидальной величины, а вторые - предназначены для подавления определенной гармоники. Сглаживающие фильтры, служащие для подавления переменной составляющей пульсирующих величин, получили основное применение в выпрямительных устройствах.
Исключительно важную роль частотные электрические фильтры играют в радиотехнике, где с их помощью решаются значительно более разнообразные задачи. Однако с этой областью их применения и существующей специальной теорией частотных фильтров в настоящем пособии учащиеся не знакомятся.
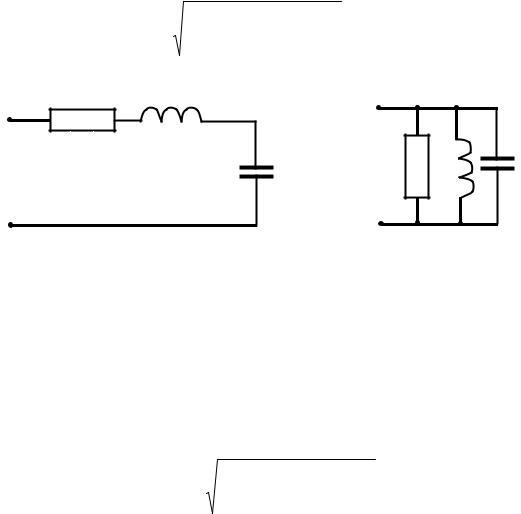
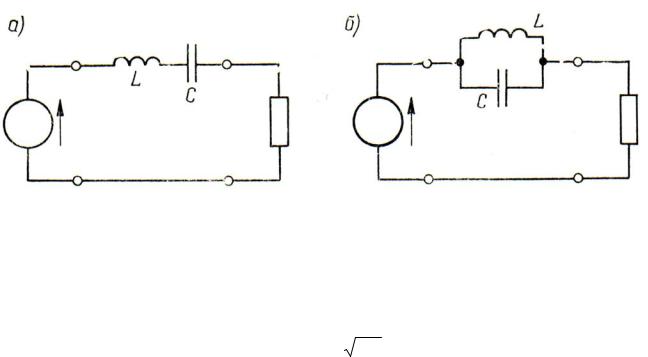
Прозрачный фильтр k -й гармоники представляет собой устройство, свободно пропускающее ток k -й гармоники и препятствующее прохождению через него токов других гармоник. Простейшим из таких фильтров является последовательный резонансный контур, включенный между источником и приемником (рис. 1.10, а) и настроенный на частоту k -й гармоники.
Рис. 1.10. Фильтры, используемые в цепях между источником и приёмником
При идеальных катушке и конденсаторе, индуктивность L и емкость С которых удовлетворяют условию резонанса при частоте k -й гармоники
k |
1 |
, |
|
LC |
|||
|
|
полное сопротивление фильтра для k -й гармоники будет равно нулю:
zk xk xLk X Ck k L |
1 |
0 , |
|
k C |
|||
|
|
и он совершенно не будет препятствовать прохождению тока этой гармоники. Для всех других гармоник фильтр будет обладать конечным реактивным сопро-

тивлением, абсолютная величина которого будет тем больше, чем дальше отстоит по номеру данная гармоника от k -й гармоники.
Действительно, реактивное сопротивление фильтра для произвольной n -
й гармоники можно представить в виде |
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
1 |
n |
|
k |
|
|
||
x |
n |
n L |
|
n L |
|
|
|
|
x |
Lk |
. |
|
n C |
1 |
|||||||||||
|
|
|
k |
|
n |
|
||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
k 2 2 L |
|
|
|
|
|
||
Например, для гармоники n , в два раза превосходящей по номеру k -ю гармонику или в два раза меньше ее, реактивное сопротивление фильтра будет в 1,5 раза больше индуктивного сопротивления xLk катушки для k -й гармоники, а для
гармоник, у которых n 4k или n k / 4, сопротивление фильтра возрастает до величины xn 3,75 xLk . При этом для всех гармоник выше
k -й ( n k ) фильтр будет иметь индуктивный характер ( xn 0 ), а для гармоник с n k он приобретет емкостный характер ( xn 0 ).
Реальный фильтр, элементы которого (в первую очередь катушка) характеризуются потерями энергии, уступает идеальному фильтру, поскольку его полное сопротивление k -й гармоники уже не будет равно нулю, а станет равным активному сопротивлению фильтра, практически равному активному сопротивлению катушки. Правда, при высокой добротности последней это сопротивление остается значительно меньше полного сопротивления фильтра токам прочих гармоник.
Заграждающий фильтр k -й гармоники должен, не препятствуя прохождению других гармоник, преградить путь для k -й гармоники тока. С этой целью в качестве фильтра используют параллельный резонансный контур, настроенный на частоту k -й гармоники и включаемый последовательно с приемником (рис. 1.10, б).
В случае идеальных элементов фильтра, удовлетворяющих условию
k |
1 |
, |
|
LC |
|||
|
|
его полная проводимость для k -ой гармоники будет равна нулю:
y |
k |
b b |
Lk |
b |
|
1 |
k C 0 , |
|
|||||||
|
k |
Ck |
|
k L |
|
||
|
|
|
|
|
|
|
то есть фильтр совершенно не пропустит ток этой гармоники. Для всех других гармоник фильтр будет обладать конечной реактивной проводимостью, абсо-
лютная величина которой будет тем больше, чем дальше отстоит по номеру данная гармоника от k -й гармоники.
Действительно, реактивную проводимость фильтра для произвольной n - й гармоники можно представить в виде
b |
|
|
1 |
n C |
1 |
|
k |
|
n |
|
|
|
n |
|
|
|
|
|
n C |
|
b |
, |
|||
n L |
1 |
|
||||||||||
|
|
|
|
n |
|
k |
Ck |
|
||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
k 2 2C |
|
|
|
|
|
|
|
повторяющем собой зависимость реактивного сопротивления прозрачного фильтра от номера гармоники. При этом для всех гармоник выше k -й ( n k ) фильтр будет иметь емкостный характер (bn 0), а для гармоник с n k он
приобретет индуктивный характер (bn 0 ).
Таким образом, рассмотренный идеальный фильтр, вполне успешно решая первую задачу — препятствовать прохождению тока гармоники, на которую он настроен, не вполне удовлетворительно справляется со второй задачей, так как он в какой-то мере препятствует прохождению токов и всех остальных гармоник.
Фильтр, составленный из реальных элементов, в которых наблюдается потеря энергии, уступает идеальному фильтру, поскольку его полная проводимость k -й гармоники уже не будет равна нулю, а окажется равной активной проводимости фильтра, практически равной активной проводимости катушки. Иными словами, такой фильтр все же будет пропускать ток k -й гармоники, хотя при достаточно высокой добротности катушки его полное сопротивление этому току будет оставаться много больше полных сопротивлений фильтра токами прочих гармоник.
Составные фильтры. С целью повышения эффективности действия реальных прозрачных и заграждающих фильтров прибегают к усложнению их схем, используя комбинацию из последовательных и параллельных резонансных контуров.
Например, для усиления действия простейшего прозрачного фильтра k -й гармоники (см. рис. 1.10, а) на его выходе параллельно приемнику включают параллельный резонансный контур L2C2 (рис. 1.11, а), настроенный на ту же
гармонику. На k-ю гармонику, для которой сопротивление этого контура будет весьма велико, такая ветвь практически не окажет влияния.
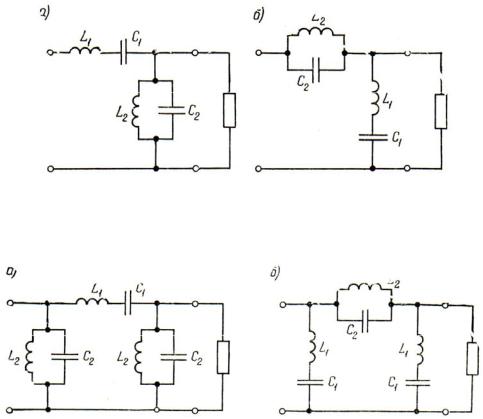
Токи же других гармоник, „просочившиеся" сквозь контур L1C1 , будут
замыкаться через нее относительно свободно, что приведет к уменьшению доли этих токов в приемнике.
Для усиления действия простейшего заграждающего фильтра k -й гармоники (см. рис. 1.10, б) параллельно приемнику на выходе фильтра включают настроенный на эту же гармонику последовательный контур L1C1 (рис. 1.11, б).
Обладая для k -й гармоники весьма незначительным сопротивлением, такая ветвь замкнет на себя почти весь „просочившийся" через контур L2C2 ток этой гармоники, дополнительно защитив от нее приемник.
Рис. 1.11. Составные фильтры в цепях несинусоидального |
пе- |
риодического тока |
|
Рис. 1.12. Дополнительные фильтры в цепях несинусоидального периодического тока
В том случае, когда питающий цепь источник обладает достаточным внутренним сопротивлением, параллельные ветви в заграждающем фильтре имеет смысл включить не только на выходе, но и на его входе (рис. 1.12). В отличие от фильтров, показанных на рис. 1.11 и называемых Г-образными, такие фильтры получили название П-образных фильтров.
В прозрачных фильтрах первой гармоники, когда ставится цель отсеить в кривой тока все высшие гармоники, пропустив в приемник только основную
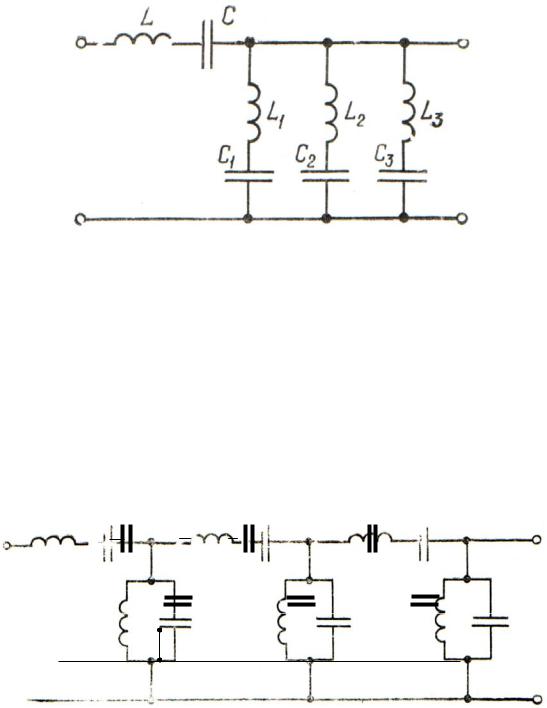
гармонику, нередко прибегают к включению на выходе фильтра параллельно приемнику нескольких прозрачных фильтров (рис. 1.13). Настраивая их на наиболее резко выраженные в кривой питающего напряжения гармоники, удается более эффективно оградить от них приемник.
Рис. 1.13. Прозрачные фильтры для нескольких гармоник тока
Цепные фильтры. Дальнейшего усиления действия фильтров возможно добиться путем последовательного соединения нескольких одинаковых фильтров. Такие фильтры получили название цепных фильтров, а отдельные повторяющиеся по схеме составные части в этом случае называют их звеньями. На рис. 1.14 для примера приведена схема трехфазного прозрачного фильтра k -й гармоники с Г-образными звеньями. Все резонансные контуры этого фильтра настроены на одну и ту же частоту.
Рис. 1.14. Пример цепного фильтра
ё
1.7. Высшие гармоники в трехфазных цепях
Последовательности гармоник. При возникновении несинусоидальных токов и напряжений в трехфазных цепях наблюдается ряд своеобразных явлений, объясняющихся тем, что различные гармоники трехфазной системы образуют собой системы с различной последовательностью фаз. Остановимся на этом вопросе подробнее.
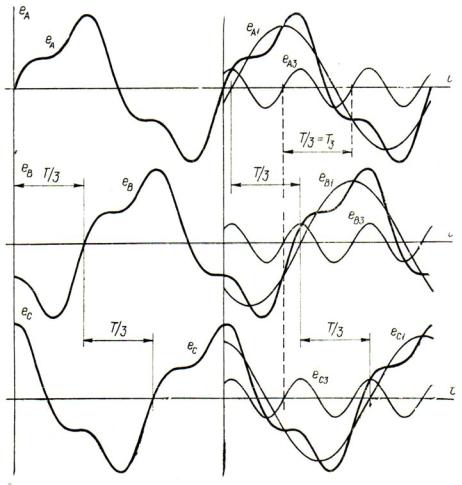
Пусть трехфазный генератор дает симметричную систему несинусоидальных ЭДС, совпадающих по форме кривой и сдвинутых друг относительно друга во времени на треть периода (см. левую половину рис. 1.15).
Рис. 1.15. Система трехфазных периодических несинусоидальных ЭДС
Предположим для простоты, что в разложении ЭДС каждой фазы, представленном в правой части рис. 1.15, кроме основной волны, имеется только одна третья гармоника. Естественно, что система eA1, eB1, eC1 первых гармоник
ЭДС также будет являться симметричной системой, в которой каждая последующая по обозначению ЭДС будет отставать от предыдущей на треть периода.
Что же касается ЭДС eA3 , eB3 , eC3 третьей гармоники, то, как следует из пра-
вой части рис. 1.15, они оказываются совпадающими друг с другом по фазе. Это обстоятельство, кажущееся на первый взгляд неожиданным, легко объяснимо, если учесть, что период T3 третьей гармоники в три раза короче периода
основной гармоники или, что то же, периода Т исходных несинусоидальных ЭДС. Поэтому сдвиг несинусоидальной функции, то есть всей совокупности соответствующих ей гармоник на одну треть периода Т соответствует в масштабе третьей гармоники сдвигу на ее полный период T3 , то есть, по существу,
отсутствию сдвига во времени отдельных ЭДС.
Распространяя полученный результат на системы любых симметричных несинусоидальных величин, приходим к выводу, что их третьи гармоники составляют в трехфазных цепях нулевые симметричные системы.
Рис. 1.16. Системы симметричных составляющих векторов
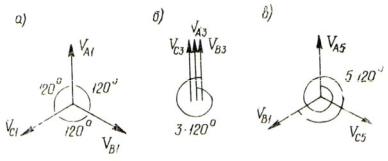
К такому же заключению нетрудно прийти, обращаясь при оценке сдвига гармоник по фазе к векторным диаграммам. Если векторы VA1, VB1, VC1 первой гармоники (рис. 1.16, а) сдвинуты друг относительно друга на углы 120° (треть периода в угловой мере), то векторы VA3 , VB3 , VC3 должны быть сдвинуты друг
относительно друга на втрое большие углы, то есть на углы 3 1200 3600 (рис. 1.16, б), или, иначе говоря, совпадать друг с другом по фазе.
Пользуясь последним приемом, мы придем к заключению, что векторы VA5 , VB5 , VC5 пятой гармоники с периодом в пять раз короче периода первой
гармоники должны быть смещены на углы 5 1200 6000 и в результате, как это следует из построений на рис. 1.16, в, составить обратную систему.
Седьмые гармоники симметричной системы несинусоидальных величин составят, как и первые гармоники, прямую систему, девятые - нулевую, одиннадцатые - обратную и т. д.
Подчеркиваем, что своеобразие явлений в трехфазных цепях при несинусоидальных токах в основном связано с особенностью проявления третьей гармоники и всех более высоких гармоник, кратных трем, составляющих, как было показано, системы нулевой последовательности.
Вращающиеся поля высших гармоник. Одним из своеобразных явлений в трехфазных цепях при несинусоидальных токах является возникновение в электрических машинах переменного тока нескольких вращающихся магнитных полей от различных гармоник тока. При этом весьма характерно, что третья и кратные ей гармоники, образующие нулевые системы, вообще не могут создавать вращающегося поля, так как последнее возникает только при условии временного сдвига между токами различных фаз.
Пятая, а также одиннадцатая, семнадцатая и т. д. гармоники с интервалом через шесть, как гармоники, образующие обратные системы, создают в машине так называемые инверсные поля, вращающиеся в противоположную сторону по сравнению с полем основной гармоники. Очевидно, что в двигателе под влиянием этих полей образуются тормозные моменты, снижающие его основной вращающий момент и тем самым ухудшающие работу двигателя. Приведенные примеры являются яркой иллюстрацией высказанного ранее положения о том, что искажение форм кривых тока влечет за собой снижение эффективности работы электротехнических устройств, и поэтому наиболее целесообразно эксплуатировать эти устройства при синусоидальных напряжениях и токах.
Особенности гармонического состава напряжений трехфазных гене-
раторов. Как уже упоминалось, ЭДС, индуктирующиеся в фазах реальных генераторов переменного тока, являются несинусоидальными и в общем случае содержат в разложении, кроме основной гармоники, полный набор нечетных высших гармоник (напомним, что четные гармоники в силу симметрии конструкций генераторов и вытекающей отсюда симметричности кривых индуктированных ЭДС в их разложении отсутствуют). При этом амплитуды гармоник, как правило, убывают по мере возрастания их номера, то есть наибольшей из всех высших гармоник в кривой фазной ЭДС генератора обычно бывает третья гармоника. Вместе с тем именно эта гармоника, а также все кратные ей гармоники полностью исчезают из линейного напряжения симметричного трехфазного генератора, как бы ярко они ни были представлены в его фазной ЭДС. Это благоприятное явление проистекает из того, что все гармоники, кратные трем, образуют нулевые симметричные системы. Однако объясняется оно по-разному в
зависимости от способа соединения обмоток генератора (звездой или треугольником).
Подчеркнем, что исчезновение третьей гармоники в линейном напряжении генератора имеет место только в случае симметричной системы его несинусоидальных ЭДС.
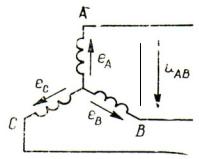
Напряжения генератора, соединенного звездой. При соединении фаз генератора звездой (рис. 1.17) линейное напряжение равно разности фазных ЭДС, например, eAB eA eB .
Рис. 1.17. Обмотки генератора соединены звездой
Поскольку фазные ЭДС третьей гармоники eA3 , eB3 , eC3 , а также все ос-
тальные гармоники, кратные трем, совпадают по фазе, их разность при симметрии системы ЭДС обращается в нуль, и линейное напряжение не содержит этих гармоник.
Таким образом, отсутствие гармоник, кратных трем, в линейном напряжении генератора при соединении его фаз звездой объясняется взаимной компенсацией ЭДС этих гармоник внутри генератора.
Напряжение генератора, соединенного треугольником. При соедине-
нии фаз генератора треугольником (рис. 1.18) линейное напряжение, равное фазному, определяется ЭДС только одной фазы, поэтому ни о какой взаимной компенсации ЭДС различных фаз аналогично предыдущему случаю на этот раз говорить нельзя. Причина исчезновения из линейного напряжения генератора всех гармоник, кратных трем, здесь кроется в другом и может быть вскрыта, если принять во внимание внутренние сопротивления фаз генератора.
Действительно, напряжение генератора каждой из гармоник, в частности, третьей гармоники, пользуясь символическим методом, в этом случае можно представить в виде уравнения источника напряжения:
U AB3 EBA3 Z И3 I BA3 ,
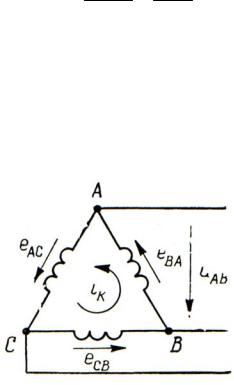
где ZИ3 – внутреннее сопротивление фазы генератора для третьей гармоники; I BA3 – ток третьей гармоники в фазе ВА.
Обращаясь к контуру генератора, нетрудно убедиться, что в нем действует сумма ЭДС всех фаз, которая для прямой и обратной систем этих ЭДС равна нулю, а для нулевой системы, какой является система совпадающих по фазе ЭДС третьей гармоники, превращается в утроенную ЭДС фазы:
EAC3 EBA3 ECB3 3EBA3 .
Под действием этой суммы в контуре генератора циркулирует ток третьей гармоники
I3 I BA3 3EBA3 EBA3 Ik3 ,
3ZИ3 Z И3
являющийся током короткого замыкания генератора, поскольку он равен ЭДС генератора, деленной на его внутреннее сопротивление. В режиме же короткого замыкания, как известно, напряжение генератора равно нулю:
U AB3 |
EBA3 Z И3 I BA3 |
EBA3 Z И3 |
EBA3 |
0 . |
|
||||
|
|
|
Z И3 |
|
Рис. 1.18. Обмотки генератора соединены треугольником
Таким образом, отсутствие гармоник, кратных трем, в линейном напряжении генератора при соединении его фаз треугольником объясняется режимом короткого замыкания генератора по этим гармоникам, когда внутреннее падение напряжения полностью компенсирует фазную ЭДС упомянутых гармоник.
Небезынтересно заметить, что к соединению фаз генераторов треугольником на практике прибегают весьма редко. И объясняется это, главным образом, именно возникновением в его контуре упомянутого выше тока короткого
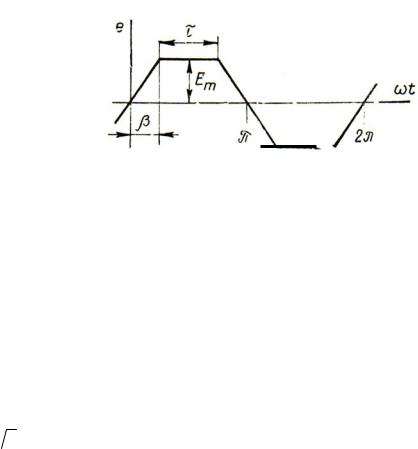
замыкания третьей гармоники, который хотя и не представляет аварийной опасности, но заметно нагружает обмотки, вызывая их дополнительный нагрев.
О возможности уменьшения пятой гармоники в напряжении генера-
тора. Форма кривой фазной ЭДС реального генератора переменного тока приближается к равнобочной трапеции (рис. 1.19), причем длина ее малого основания определяется шириной магнитного полюса машины. Разложение трапецеидальной функции в гармонический ряд имеет вид (рис. 1.3, б)
|
4E |
|
|
1 |
|
1 |
|
e |
|
m sin sin t |
|
sin 3 sin 3 t |
|
sin 5 sin 5 t ... . |
|
|
9 |
25 |
|||||
|
|
|
|
|
|||
Таким образом, выбором определенного значения угла , иначе говоря, изменением ширины полюса машины представляется возможность исключить из разложения одну из гармоник. Например, при 2 / 3 обращается в нуль sin 3 и исчезает третья гармоника, а при 2 / 5 пропадает пятая гар-
моника (sin 5 0 ).
Рис. 1.19. Форма кривой ЭДС реального генератора
Поскольку в линейном напряжении трехфазного генератора третья гармоника не проявляется, конструкторам представляется возможность, не заботясь о ней, принять меры к устранению следующей по величине 5-й гармоники. В этом случае наибольшей из гармоник будет являться седьмая, которая в разложении трапеции выражена уже сравнительно слабо.
Соотношение между действующими линейным и фазным напряже-
ниями в случае симметрии их систем в четырехпроводной трехфазной сети при наличии высших гармоник в общем случае может отличаться от привычного
значения  3 . Если фазная ЭДС генератора содержит гармоники, кратные трем, то они будут присутствовать и в фазном напряжении сети, действующее значе-
3 . Если фазная ЭДС генератора содержит гармоники, кратные трем, то они будут присутствовать и в фазном напряжении сети, действующее значе-
ние которого определится через действующие значения его гармоник выражением
UФ  Uф21 Uф23 Uф25 Uф2 7 Uф29 Uф211 ... .
Uф21 Uф23 Uф25 Uф2 7 Uф29 Uф211 ... .
В линейном же напряжении гармоники, кратные трем, будут отсутствовать и его действующее значение представится через действующее значение гармоник в виде
U Л 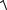 U Л2 1 U Л2 5 U Л2 7 Uф211 ... .
U Л2 1 U Л2 5 U Л2 7 Uф211 ... .
Поскольку между действующими фазными и линейными напряжениями в пределах каждой гармоники остаются справедливыми соотношения
U Л1 3UФ1 , |
U Л5 3UФ5 и т. д., |
то отношение действующего линейного напряжения к действующему фазному напряжению
U |
Л |
|
U Л2 |
1 |
U Л2 5 |
U Л2 7 |
U Л2 11 ... |
|
UФ |
UФ21 UФ2 3 |
UФ2 5 |
UФ2 7 |
UФ2 9 UФ211 ... |
||||
|
||||||||
окажется меньше чем  3 (U Л /UФ
3 (U Л /UФ  3 ).
3 ).
Высшие гармоники в приемниках. Переходя к особенностям проявления высших гармоник в трехфазных приемниках, подчеркнем, что, как и в генераторах, основное своеобразие наблюдается в поведении третьей и остальных кратных ей гармоник, которые образуют системы нулевой последовательности. Напомним, что последние характеризуются лишь плоскостной симметрией и резко отличаются по своим свойствам от систем с центральной симметрией, которые образуются всеми прочими гармониками. Рассмотрим несколько наиболее важных, связанных с этим обстоятельством явлений.
Ток в нейтральном проводе. Известно, что при синусоидальных линейных токах ток в нейтральном проводе в случае симметричного режима приемника равен нулю. При несинусоидальных токах это привычное положение может быть нарушено и в нейтральном проводе даже в симметричном режиме иногда появляется достаточно большой ток. Это случается, когда в фазных напряжениях сети присутствуют гармоники, кратные трем, вызывающие соответствующие токи в фазах приемника. При этом ток в нейтральном проводе (рис. 1.20), равный сумме линейных токов
inN iA iB iC ,
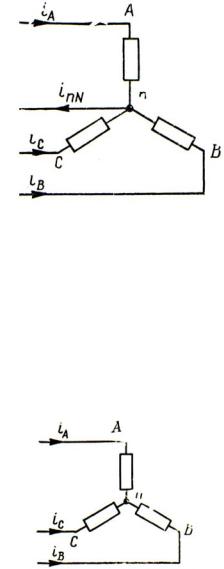
будет целиком состоять из гармоник, кратных трем, так как токи всех остальных гармоник, включая и основную волну, образующие системы с центральной симметрией, складываясь, дадут ноль. Токи третьей и всех кратных ей гармоник, образующие нулевые симметричные системы с плоскостной симметрией, при сложении дадут утроенные значения токов отдельных фаз. Таким образом, в нейтральном проводе будет протекать несинусоидальный ток
inN 3iФ3 3iФ9 3iФ15 ...,
состоящий из утроенных значений токов третьей, девятой, пятнадцатой и т. д. гармоник фаз приемника. Так как первой гармоники тока в нейтральном проводе не будет, то третья гармоника приобретает в нем роль основной волны, то есть ток в нейтральном проводе будет иметь утроенную частоту по сравнению с токами фаз.
Рис. 1.20. Трехфазный приемник, включённый звездой с нулевым |
про- |
водом |
|
Линейные токи в цепи без нейтрального провода при симметричном режиме не могут содержать гармоник, кратных трем, что непосредственно вытекает из уравнения, записанного в этом случае по первому закону Кирхгофа для нейтральной точки n (рис. 1.21).
iA iB iC 0 .
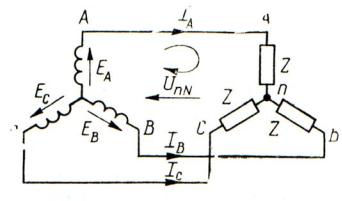
Рис. 1.21. Трехфазная цепь без нейтрального провода
Действительно, прибегая к доказательству „от противного", предположим, что гармоники, кратные трем, существуют. Тогда как токи, совпадающие по фазам в трех проводах цепи, они должны были бы дать в сумме результат, отличный от нуля. Поскольку же сумма линейных токов все же равна нулю, мы должны прийти к выводу об отсутствии токов третьей и всех кратных ей гармоник в линейных проводах цепи без нейтрального провода.
Подчеркнем, что сформулированное положение, которое мы только что доказали для приемника, соединенного звездой, остается справедливым и в случае приемника, соединенного треугольником, так как для последнего сохраняется равенство нулю трех линейных токов.
Напряжение между нейтральными точками приемника и источника в симметричном режиме при синусоидальных токах даже при отсутствии нейтрального провода равно нулю. При наличии же в фазных ЭДС источника гармоник, кратных трем, они полностью проявятся в напряжении между нейтральными точками, в частности, и при симметричном режиме. Для доказательства этого положения обратимся к контуру одной фазы цепи, например фазы А (рис. 1.22), и, используя второй закон Кирхгофа, составим по этому контуру уравнение для третьей гармоники напряжений и ЭДС:
Z3I A3 UnN 3 EA3 .
Рис. 1.22. Схема трехфазной электрической цепи
Так как в звезде без нейтрального провода токи третьей гармоники существовать не могут, то из предыдущего уравнения получим
UnN 3 EA3 .
Аналогичный результат мы получим для всех гармоник, кратных трем, в то время как остальные гармоники, образующие, как и основная гармоника, системы с центральной симметрией, ничего не внесут в это напряжение. Таким
образом, напряжение между нейтральными точками будет содержать только гармоники, кратные трем, равные соответствующим фазным ЭДС генератора:
unN eФ3 eФ9 eФ15 ....
Так как первая гармоника в этом напряжении будет отсутствовать, то третья гармоника примет в этом напряжении роль основной гармоники, и, следовательно, это напряжение, являясь несинусоидальным, будет иметь тройную частоту по сравнению с частотой ЭДС генератора.
Фазные токи треугольника, в принципе, могли бы содержать гармоники, кратные трем, однако в линейном приемнике при симметричном режиме они не могут возникнуть из-за отсутствия этих гармоник в линейных напряжениях источника, которые при соединении приемника треугольником одновременно являются и его фазными напряжениями.
Тесты для самопроверки
1. Мгновенное значение несинусоидального напряжения представлено в виде ряда
u 4 3 2sin( t 3) 1,41sin(2 t 4). Чему равно действующее значение
2sin( t 3) 1,41sin(2 t 4). Чему равно действующее значение
напряжения?
а. 5,1 В. б. 3 В. в. 1,41 В. г. 8 В.
2. Известны несинусоидальные ток i и напряжение u на входе цепи:
i 2 4  2sin( t 20 ) 2
2sin( t 20 ) 2  2sin( 2 t 13 )
2sin( 2 t 13 )  2 sin (3 t 17 ), u 2 8
2 sin (3 t 17 ), u 2 8 2sin( t 35 ) 4
2sin( t 35 ) 4 2sin( 2 t 63 ) 2
2sin( 2 t 63 ) 2 2sin(3 t 37 ).
2sin(3 t 37 ).
Чему равна полная |
мощность? |
|
|
|
а. 23 В·А. |
б. 46 В·А. |
в. 0 В·А. |
г. 4 В·А. |
|
3. Для цепи дано X L L 3Ом, |
R 4, |
X C 1 |
С 4 Ом; |
|
u 10 5 2sin t 2
2sin t 2 2sin3 t . Определите постоянную составляющую тока на входе цепи.
2sin3 t . Определите постоянную составляющую тока на входе цепи.
а. 2,5 А |
i |
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
u |
L |
|
|
|
R |
||||||
|
|
|
|||||||||
б. 0,9 А. |
|
|
|
||||||||
в. 1,4 А. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г. 0 А. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Для цепи дано X L L 3 Ом, R 4 Ом, |
X C 1 С 4 Ом, |
||||||||||
u 10 5 2 sin t 2
2 sin t 2 2 sin 3 t . Определите постоянную составляющую тока на входе цепи.
2 sin 3 t . Определите постоянную составляющую тока на входе цепи.
а. 2,5 А |
|
|
i |
L |
|
||||
б. 0,9 А. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в. 1,4 А. |
u |
|
|
C |
R |
|
|
||
|
|
|
|
||||||
|
|
|
|
||||||
г. 0 А. |
|
|
|
|
|
|
|
|
|
5. Мгновенное значение несинусоидального напряжения представлено в виде ряда
u 8 3 2sin( t 3) 1,41sin(2 t 4). Чему равно действующее значение
2sin( t 3) 1,41sin(2 t 4). Чему равно действующее значение
напряжения? |
|
|
|
а. 5,1 B. |
б. 3 B. |
в. 1,41 B. |
г. 8,6 B. |
6.Чему равна активная мощность в цепи при несинусоидальных токе и напряжении?
а. Сумме постоянной мощности и активных мощностей всех гармоник. б. Активной мощности первой гармоники.
в. Сумме активных мощностей всех гармоник. г. Постоянной мощности.
7.Известны несинусоидальные ток i и напряжение u на входе цепи:
i 2 sin( t 20 ) 2
2 sin( t 20 ) 2 2 sin(2 t 13 ) 2
2 sin(2 t 13 ) 2 2 sin(3 t 17 ),
2 sin(3 t 17 ),
u 2  2 sin(4 t 35 ) 2
2 sin(4 t 35 ) 2 2 sin(5 t 63 ) 2
2 sin(5 t 63 ) 2 2 sin(6 t 37 ).
2 sin(6 t 37 ).
Чему равна полная |
мощность? |
|
|
а. 15 В·А. |
б. 9 В·А. |
в. 0 В·А. |
г. 8 В·А. |
8.Если ток емкости i 2sin ωt 2sin 2ωt , то амплитуда первой гармоники напряжения будет больше амплитуды второй гармоники напряжения в… а. 2 раз. б. 8 раз. в. 4 раза. г. 1,5 раза.
9.Чему равно комплексное сопротивление цепи на частоте второй гармоники,
если на частоте первой гармоники R=10 Ом, |
X L (ω) 5 Ом, XC (ω) 20 Ом… |
|||||||
а. 10e j90 |
L |
|||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
б. |
|
L |
|
|
|
|||
в. 10e j450 |
|
|
R |
|||||
С |
|
|
|
|
|
|||
г. 35e j45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. Если ток индуктивности L=0,1 Гн, i 5sin(100t 60 ) 1sin(200t 30 ) , то напряжение u равно…
а. u 50sin(100t 150 ) 20sin(200t 120 )
б. u 50sin(100t 150 ) 10sin(200t 60 )
в. u 10sin(100t 30 ) 10sin(200t 30 )
г. u 50sin(100t 30 ) 20sin(200t 60 )
11.Линейные токи в цепи без нейтрального провода при симметричном режиме не могут содержать гармоник… а. Кратных двум. б. Кратных трем. в. Кратных четырем. г. Кратных пяти.
12.Напряжение между нейтральными точками симметричных приемника и ис-
точника при наличии фазных ЭДС источника гармоник, кратных трем … |
|
а. Равно нулю б. Не равно нулю в. Для ответа недостаточно данных. |
г. |
Фазному напряжению |
|
ГЛАВА 2. НЕЛИНЕЙНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА
2.1. Нелинейные элементы цепи
Электрическая цепь, в которую входит хотя бы один нелинейный элемент, обтекаемый током, называется нелинейной цепью. В отличие от элементов линейных цепей с постоянными параметрами параметры нелинейных элементов зависят от токов и напряжений. Свойства таких элементов нельзя определить с помощью одного постоянного параметра, а необходимо задавать зависимости между переменными (током и напряжением), называемые характеристиками элементов, во всем диапазоне изменения переменных. Характеристики элементов обычно определяются экспериментально и изображаются в виде графиков. Графики могут быть приближенно представлены аналитически, обычно в виде полиномов.
Как и линейные элементы, нелинейные подразделяются на резистивные, индуктивные и емкостные элементы. По числу внешних выводов различают элементы двухполюсные, четырехполюсные и многополюсные. Далее характеристики элементов могут быть неизменными во времени (инвариантными) или
изменяющимися во времени (переменными). Основное внимание при дальнейшем рассмотрении уделим двухполюсным элементам.
Относительность границ между линейными и нелинейными элемен-
тами. Следует иметь в виду, что деление элементов электрических цепей на линейные и нелинейные в известной степени относительно. На практике мы весьма редко встречаемся со строго линейными характеристиками. Чаще они лишь в той или иной мере приближаются к прямой линии. На рис. 2.1 (кривые 2, 3, 4) приведены примеры вольт-амперных характеристик нелинейных резистивных приемников, а примеры внешних характеристик нелинейных источников представлены на рис. 2.2 (кривые 2,3,4).
а) б)
Рис. 2.1. Вольт-амперные характеристики нелинейных приемников
Рис. 2.2. Внешние характеристики нелинейных источников
Поэтому решение вопроса о принадлежности таких элементов к одной или другой группе зависит от того, насколько строго мы подходим к оценке формы характеристик. Строгость же определяется желаемой точностью расчета режима в рассматриваемом элементе, и, следовательно, один и тот же элемент при грубых прикиданных расчетах может считаться линейным, а в случае точных расчетов его следует отнести к нелинейным элементам. Так как исследова-
ние и расчет нелинейных цепей сопряжены, как правило, с большими трудностями, чем аналогичные задачи линейных цепей, то во всех случаях, когда линейный закон достаточно близко отражает действительную вольт-амперную характеристику данного приемника, предпочитают рассматривать его как линейный элемент.
В тех случаях, когда на электрической схеме необходимо подчеркнуть нелинейность того или иного элемента электрической цепи, его графическое изображение перечеркивают ломаной линией, как показано на рис. 2.1, а и б, на первом из которых приведено общее графическое изображение нелинейного приемника, а на втором — нелинейного источника.
Нелинейные резистивные элементы. Поскольку в нелинейных рези-
стивных элементах линейная связь между током и напряжением отсутствует, понятия о сопротивлении и проводимости этих элементов, как коэффициентах пропорциональности между током и напряжением, строго говоря, теряют смысл. Однако на практике указанные понятия искусственно сохраняют, определяя, в частности, сопротивление нелинейного резистора (приёмника) как отношение напряжения U на приемнике к его току I и называют его статическим сопротивлением:
R |
|
U . |
(2.1) |
||
СТ |
|
I |
|
||
|
|
|
|
||
Отношение бесконечно малых приращений напряжения и тока называют |
|||||
дифференциальным сопротивлением: |
|
||||
R |
|
dU |
. |
(2.2) |
|
|
|||||
d |
|
|
d I |
|
|
|
|
|
|
||
Оба из упомянутых сопротивлений не являются для данного нелинейного приемника постоянными величинами, а изменяются, и иногда в весьма широких пределах, в зависимости от режима работы приемника, то есть от его напряжения или протекающего по нему тока. Для уяснения этого важного обстоятельства обратимся к графической интерпретации обоих сопротивлений на вольт-амперной характеристике приемника (рис. 2.3).
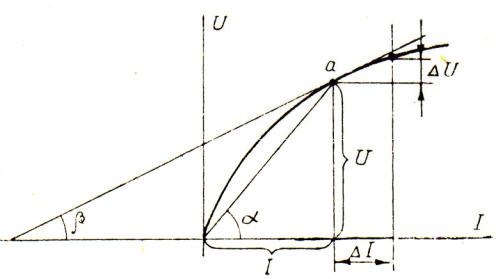
Рис. 2.3. Вольт-амперная характеристика нелинейного приёмника
Если остановиться на каком-либо определенном режиме работы нелинейного приемника, соответствующем некоторой рабочей точке а на его вольтамперной характеристике, то понятие интегрального сопротивления RСТ легко
связать с тангенсом угла между лучом, проведенным из начала координат в рабочую точку, и осью тока:
R U k tg , |
(2.3) |
СТ I
где k — коэффициент, зависящий от принятых на чертеже масштабов напряжения и тока.
Аналогично понятие о дифференциальном сопротивлении нетрудно связать с тангенсом угла между касательной, проведенной к вольт-амперной характеристике в рабочей точке, и осью тока (см. рис. 2.3):
R |
dU |
|
lim |
U |
k tg |
|
|
|
|
|
|
|
|
||||
d |
d I |
|
|
I |
, |
(2.4) |
||
|
|
|
|
|||||
|
|
|
|
I 0 |
|
|
||
причем значение коэффициента k |
в этом соотношении совпадает с его значе- |
|||||||
нием в предыдущем выражении. |
|
|
|
|
|
|
|
|
Предположим теперь, что режим работы приемника изменяется и рабочая точка перемещается вдоль его характеристики (см. рис. 2.3). Тогда в силу нелинейности этой характеристики будет меняться положение упомянутых луча и касательной, что вызовет изменения углов и и, следовательно, изменения статического и дифференциального сопротивлений приемника. В частности, в
приемнике с вольт-амперной характеристикой, представленной на рис. 2.3, отклонение от рассмотренного режима, соответствующего рабочей точке а, в сторону увеличения тока вызовет уменьшение обоих сопротивлений, а изменение режима в сторону уменьшения тока приведет к увеличению этих сопротивлений.
К понятию статического сопротивления, то есть к выражению (2.1), прибегают в тех случаях, когда необходимо определить ток в нелинейном приемнике по известному напряжению или, наоборот, рассчитать напряжение по заданному току приемника. Если же возникает задача найти приращение тока в приемнике, вызванное незначительным приращением напряжения, или, наоборот, определить изменение напряжения по небольшому изменению тока приемника, то в этом случае необходимо обратиться к дифференциальному сопротивлению, используя выражение (2.2).
Заметим, что в линейных приемниках понятия статического и дифференциального сопротивлений совпадают и необходимость оперирования двумя понятиями сопротивлений отпадает.
Проводимости нелинейных резистивных приемников. Наряду со ста-
тическим и дифференциальным сопротивлениями для нелинейных приемников вводят понятия статической и дифференциальной проводимостей, определяемых соотношениями
G |
I |
|
1 |
; G |
|
|
d I |
|
I |
, |
U |
R |
|
dU |
R |
||||||
СТ |
|
|
d |
|
|
|
||||
|
|
|
СТ |
|
|
|
|
|
d |
|
однако они находят весьма ограниченное применение.
Нелинейные индуктивные элементы. Условное обозначение нелиней-
ного двухполюсного индуктивного элемента изображено на рис. 2.4, а. Основной характеристикой элемента является вебер-амперная характеристика — зависимость потокосцепления от тока или тока от потокосцепления
Ψ fL i ; |
i fL 1 Ψ . |
(2.5) |
Потокосцепление и напряжение связаны соотношениями
t |
u d Ψ . |
|
Ψ u d t ; |
(2.6) |
|
|
d t |
|
|
|
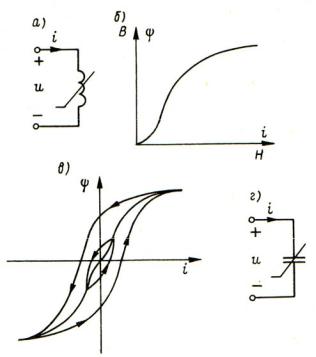
Рис. 2.4. Нелинейная индуктивная катушка
Из соотношений (2.5) и (2.6) следует очень важный вывод о непрерывности потокосцепления в индуктивном элементе: при конечном напряжении потокосцепление в индуктивности не может изменяться скачком — является непрерывной величиной. Действительно, для момента t t0
Ψ t0 Ψ t0 |
t0 |
|
u d t Ψ t0 . |
(2.7) |
t0
B случае пассивного индуктивного элемента вебер-амперная характеристика располагается в первом и третьем квадрантах. Энергия, потребляемая таким элементом, положительна:
t |
|
W t u i d t i d 0 |
|
|
0 |
в силу совпадения знаков обеих переменных.
Обычным нелинейным индуктивным элементом является катушка индуктивности, расположенная на замкнутом ферромагнитном сердечнике. Веберамперная характеристика определяется кривой намагничивания стали сердечника — зависимостью индукции от напряженности магнитного поля. На рис. 2.4, б изображена кривая начального намагничивания, снимаемая при медленном нарастании индукции в предварительно размагниченном материале. При
симметричном периодическом намагничивании получаются гистерезисные петли (рис. 2.4, в), вершины которых располагаются на основной кривой намагничивания. Вебер-амперная характеристика обычного индуктивного элемента получается многозначной, сложным образом зависящей от предыстории процессов. При несимметричном намагничивании получаются несимметричные кривые намагничивания, называемые частными петлями.
При наличии нескольких катушек на ферромагнитном сердечнике получим нелинейный многополюсный элемент.
Нелинейные емкостные элементы. Условное обозначение нелинейного емкостного элемента показано на рис. 2.4, г. Основная кулон-вольтная характе-
ристика элемента выражается так: |
u fC 1 q . |
|
q fC u ; |
(2.8) |
|
Заряд и ток элемента связаны соотношениями |
|
|
t |
i d q . |
|
q i d t ; |
(2.9) |
|
|
d t |
|
|
|
|
Отсюда следует также очень важный вывод о непрерывности заряда в емкостном элементе: при конечном токе заряд представляет собой непрерывную
функцию, т. е. не может изменяться скачком; для момента t t0 |
имеем |
||
q t0 q t0 |
t0 |
|
|
i d t q t0 |
. |
(2.10) |
|
t0
Если кулонвольтная характеристика элемента располагается в первом и третьем квадрантах, в которых знаки заряда и напряжения совпадают, то имеем пассивный элемент. Энергия, потребляемая элементом, здесь неотрицательна:
t |
q |
W t i u dt u d q 0 . |
|
|
0 |
Обычными нелинейными емкостными элементами являются электрический конденсатор из диэлектрика (диэлектрическая проницаемость которого зависит от напряженности электрического поля), а также барьерная емкость обратно смещенного p n -перехода полупроводникового диода. Важное досто-
инство барьерной емкости состоит в применимости ее до очень высоких частот.
2.2. Нелинейные элементы в цепях постоянного тока при исследовании статических процессов
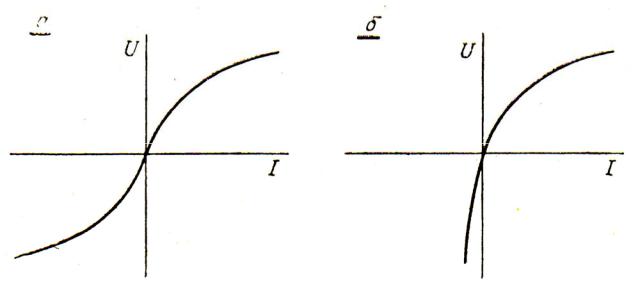
В цепях постоянного тока при исследовании статических процессов наибольший интерес представляют резистивные элементы, которые являются потребителями электрической энергии. Индуктивные и емкостные элементы не потребляют электрической энергии, а поэтому в дальнейшем остановимся лишь на рассмотрении резистивных элементов.
Симметричные и несимметричные приемники. Нелинейные приемни-
ки по их реакции на изменение направления тока разделяют на симметричные и несимметричные приемники.
Симметричными приемниками называют такие приемники, свойства которых не зависят от направления тока в них. Поэтому вольт-амперные характеристики симметричного приемника, снятые при разных направлениях тока в нем, будут одинаковы и при построении в двух квадрантах, соответствующих разным направлениям тока (рис. 2.5, а), изобразятся двумя ветвями, симметричными относительно начала координат.
Заметим попутно, что все линейные приемники относятся к симметричным приемникам.
Несимметричные приемники реагируют на токи различного направления по-разному, а поэтому их вольт-амперные характеристики являются относительно начала координат несимметричными кривыми (рис. 2.5, б).
Рассмотрим несколько характерных примеров симметричных и несимметричных приемников.
Рис. 2.5. Симметричные и несимметричные источники
Лампа накаливания. Наиболее знакомым для учащихся симметричным нелинейным приемником является лампа накаливания, графическое изображе-
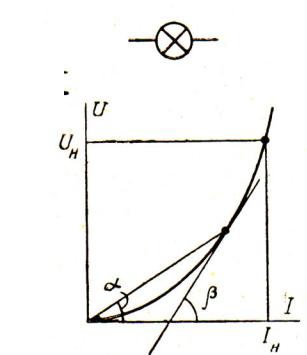
ние которой на схемах приведено на рис. 2.6, а. Вольт-амперная характеристика лампы, представленная на рис. 2.6, б, показывает, что по мере увеличения тока ее интегральное сопротивление увеличивается. Как известно из курса физики, последнее объясняется увеличением температуры нити лампы по мере усиления тока в ней и происходящим в связи с этим возрастанием удельного сопротивления металла (вольфрама), из которого сделана нить. Различие в интегральных сопротивлениях горячей (при номинальном напряжении) и холодной ламп (при весьма малом токе) довольно значительно и иногда достигает десятикратного значения.
а)
б)
Рис. 2.6. Вольт-амперная характеристика лампы накаливания
Дифференциальное сопротивление лампы увеличивается с возрастанием тока еще быстрее (см. изменение угла на рис. 2.6, б), оставаясь всегда больше интегрального сопротивления ( ). Лишь при весьма малых токах, когда рабочая точка располагается на характеристике вблизи начала координат, можно говорить о равенстве интегрального и дифференциального сопротивлений, так как направления луча и касательной в этом случае совпадают.
Бареттор. Оригинальной модификацией лампы накаливания является бареттор — прибор, конструктивно отличающийся от лампы накаливания тем, что вместо вольфрамовой в нем использована стальная нить, а баллон баретто-
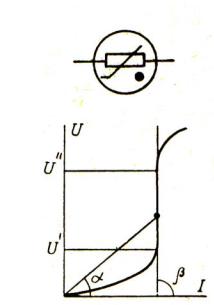
ра заполнен не инертным газом, а водородом. Этим достигают того, что в вольт-амперной характеристике бареттора образуется практически вертикальныйучасток (рис. 2.7, б), в пределах которого (от напряжения U до напряжения U ) изменение напряжения не вызывает заметного изменения тока. Именно это свойство бареттора и используется на практике в тех случаях, когда требуется поддержать неизменное значение тока в цепи при колеблющемся питающем напряжении.
а)
б)
Рис. 2.7. Вольт-амперная характеристика бареттора
Графическое изображение бареттера на электрических схемах приведено на рис. 2.7, а, где прямоугольник, перечеркнутый ломаной линией, поясняет, что бареттер, по существу, является нелинейным резистором, окружность указывает на конструктивное оформление бареттера в баллоне, а точка свидетельствует о наполнении этого баллона газом.
С теоретической точки зрения бареттер интересен тем, что его дифференциальное сопротивление на участке стабилизации тока весьма велико и в идеальном случае (при строго вертикальном участке характеристики) обращается в бесконечность 0,5 .
Варистор. Значительной нелинейностью вольт-амперной характеристики (рис. 2.8, б) обладают полупроводниковые резисторы, получившие особое название – варисторы. Сопротивление варисторов зависит главным образом от напряженности электрического поля в полупроводнике и, следовательно, от на-
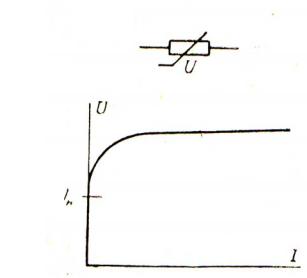
пряжения на зажимах прибора, резко уменьшаясь при достижении определенных значений. Поэтому в условном обозначении варистора (рис. 2.8, а) фигурирует буква U (зависимость сопротивления от напряжения).
а)
б)
UН
Рис. 2.8. Вольт-амперная характеристика варистора
Применяются варисторы чаще всего в качестве приборов, защищающих электрические установки от перенапряжений. Так как при нормальном напряжении U H на варисторе его ток ничтожно мал (рис. 2.8, б), то включение вари-
стора параллельно защищаемому устройству практически не изменяет его режима. При возрастании же напряжения выше определенных границ ток варистора резко увеличивается, вызывая соответствующее увеличение падения напряжения в других участках цепи, ограничивая тем самым чрезмерное повышение напряжения на защищаемом устройстве.
Полупроводниковый терморезистор. Весьма своеобразно выглядит вольт-амперная характеристика полупроводникового терморезистора, представляющего резистор, сопротивление которого зависит от температуры, резко уменьшаясь с ее увеличением. Температурная зависимость сопротивления терморезистора является его основной эксплуатационной характеристикой, в связи с чем к графическому обозначению терморезистора в виде нелинейного рези-
стора (рис. 2.9, а) добавлен буквенный символ температуры t0 . Однако здесь остановимся только на вольт-амперной характеристике терморезистора, показанной на рис. 2.9, б и отличающейся от всех ранее рассмотренных характеристик наличием так называемого падающего участка (вправо от точки а), на ко-
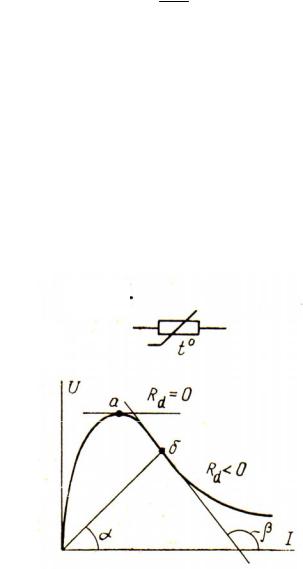
тором увеличению тока соответствует не увеличение напряжения, как обычно, а его уменьшение. Характерно, что дифференциальное сопротивление терморезистора на падающем участке приобретает отрицательное значение:
Rd ddUI 0 ,
поскольку при положительном приращении d I тока имеет место отрицательное приращение d U напряжения. В точке а дифференциальное сопротивление обращается в нуль, так как касательная к характеристике терморезистора принимает горизонтальное положение ( 0 ). При увеличении тока от этого режима дифференциальное сопротивление сначала (до режима, соответствующего точке б перегиба на характеристике) по абсолютной величине возрастает, а затем, оставаясь отрицательным, монотонно падает. Интегральное сопротивление терморезистора в пределах всей характеристики положительно, меняется монотонно и имеет наибольшее значение при бесконечно малом токе.
а)
б)
Рис. 2.9. Вольт-амперная характеристика полупроводникового |
термо- |
резистора |
|
Полупроводниковый вентиль. Примером несимметричного нелинейного элемента может служить полупроводниковый вентиль, резко меняющий свою проводимость при изменении направления прикладываемого к нему напряжения. В прямом направлении вентиль сравнительно легко проводит ток, и даже относительно большому прямому току (в мощных вентилях до сотен амперов) соответствует весьма незначительное прямое напряжение (порядка десятых до-
лей вольта). Наоборот, в обратном направлении ток встречает большое сопротивление, и даже при относительно высоких обратных напряжениях (несколько сот вольтов) обратный ток вентиля остается крайне малым (миллиамперы). В связи с этим вольт-амперную характеристику полупроводниковых вентилей принято при различных направлениях тока и напряжения строить в различных масштабах по обеим осям, как это показано, например, на рис. 2.10, в. Если же характеристику вентиля построить в одинаковых масштабах в области прямых (положительных) и обратных (отрицательных) токов и напряжений, то ее положительная и отрицательная ветви практически сольются соответственно с осью тока и осью напряжения (рис. 2.10, б). Характеристикой, точно совпадающей с осями координат, обладает так называемый идеальный вентиль, абсолютно свободно пропускающий ток в одном направлении и совершенно не пропускающий его в обратном направлении. К понятию идеального вентиля часто прибегают при анализе работы сложных -вентильных схем, содержащих большое количество вентилей.
Обратим внимание на то, что вольт-амперную характеристику вентиля принято изображать, откладывая по оси абсцисс напряжение, а по оси ординат ток, как это показано на рис. 2.10.
Графическое изображение полупроводникового вентиля представляет собой треугольник с чертой у одной из вершин (рис. 2.10, а), причем прямое, то есть легко проводящее направление вентиля, соответствует направлению стрелки, образованной сочетанием треугольника и подводящего провода (на рис. 2.10, а слева направо).
С теоретической точки зрения на характеристике диода интересно отметить две точки. В точке а, где луч, проведенный из начала координат, касается характеристики диода, его интегральное сопротивление принимает минимальное значение. А в точке б, являющейся точкой перегиба вольт-амперной характеристики, минимальным становится дифференциальное сопротивление диода.
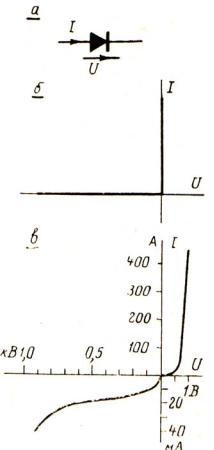
Рис. 2.10. Вольт-амперная характеристика полупроводникового вентиля
Параметры нелинейных источников. Обращаясь к нелинейным источ-
никам, заметим, что такие важные параметры, как электродвижущая сила Е и исходный ток J источника, и в нелинейных источниках принято считать постоянными величинами, соответственно равными напряжению U0 холостого
хода и току I K короткого замыкания, |
|
E U0 ; |
J IK . |
Что же касается внутреннего сопротивления или внутренней проводимости нелинейных источников, то в связи с нелинейностью их внешней характеристики, как и в приемниках, приходится вводить понятия о двух внутренних сопротивлениях или двух внутренних проводимостях — статических и дифференциальных. При этом каждая из упомянутых величин не является для данного источника постоянной, а меняется в зависимости от режима его работы.
Под статическим внутренним сопротивлением понимают величину, на которую следует умножить ток источника, чтобы после вычитания полученного произведения из ЭДС получился результат, равный напряжению источника в

данном режиме. Иначе говоря, статическое внутреннее сопротивление должно удовлетворять знакомому нам уравнению источника
U E RСТ.Н I
при любом режиме его работы, то есть определяться выражением
RСТ.H E I U .
При этих условиях статическое внутреннее сопротивление будет графически отражаться тангенсом угла (рис. 2.11) между направлением оси тока и лучом, проведенным из точки холостого хода в рабочую точку внешней характеристики источника, соответствующую заданному режиму работы источника,
RСТ.H k tg ,
где k — коэффициент, зависящий от выбора масштабов по осям. Дифференциальным внутренним сопротивлением источника называют
взятую с обратным знаком производную от напряжения источника по его току
RИd ddUI k tg
и пропорциональную тангенсу угла наклона касательной, проведенной к внешней характеристике источника в рабочей точке (рис. 2.11).
Понятием статического внутреннего сопротивления на практике пользуются, когда с помощью уравнения источника хотят вычислить его напряжение по заданному току или рассчитать ток при известном напряжении источника. К понятию же дифференциального внутреннего сопротивления прибегают в тех случаях, когда возникает необходимость рассчитать изменение напряжения источника при небольшом изменении его тока:
U RИd I .
Рис. 2.11. Источник с опускающейся начальной частью характеристики
Рис. 2.12. Источник с поднимающейся начальной частью характеристики
Заметим, что для источников с поднимающейся начальной частью характеристики (рис. 2.12), с чем нередко приходится встречаться на практике, статическое и дифференциальное внутренние сопротивления на приподнятом участке приобретают отрицательное значение (статическое на участке от точки холостого хода до точки б, а дифференциальное — от точки холостого хода до точки а). В точке а дифференциальное, а в точке б статическое внутренние сопротивления обращаются в нуль.
Понятиями статической и дифференциальной внутренних проводимостей на практике пользуются очень редко, и поэтому здесь на них подробно останавливаться не будем.
Эквивалентные схемы нелинейных источников. При расчетах цепей с нелинейными источниками часто прибегают к их представлению согласно эквивалентным схемам линейных источников в виде совокупности двух элементов — идеального источника и резистора. В зависимости от избранной эквивалентной схемы можно говорить или о последовательном соединении идеального источника напряжения Е (рис. 2.13, а) с ЭДС, равной напряжению холостого хода нелинейного источника, и резистора RИ , отражающего внутреннее сопро-
тивление источника, или о параллельном соединении идеального источника тока J (рис. 2.13, б) с исходным током, равным току короткого замыкания нелинейного источника, и резистора GИ как эквивалента внутренней проводимости
источника. Очевидно, оба резистора будут являться в этом случае нелинейными. Идеальные же источники окажутся источниками с постоянными парамет-
рами Е или J , то есть линейными элементами. Таким образом, указанный прием позволяет любой нелинейный источник заменить в схеме идеальным источником и нелинейным резистором (приемником).
а)
б)
Рис. 2.13. Идеальные источники с нелинейными приемниками
Нелинейный источник напряжения. Останавливаясь на последовательной эквивалентной схеме, нашедшей преимущественное распространение, представим напряжение U нелинейного источника в виде
U E RСТ.И I E U И ,
сосредоточив внимание на внутреннем напряжении U И RСТ.И I , которое в данном случае удобно рассмотреть как напряжение на нелинейном резисторе
RИ .
На характеристике источника (рис. 2.14, а) зависимость этого напряжения U И E U от тока определяется совокупностью ординат, показанных на рис.
2.14, а штриховкой.
а)
б)
Рис. 2.14. Нелинейный источник напряжения
Аналогичной зависимостью должен характеризоваться и нелинейный резистор RИ , вольт-амперная характеристика которого, как вытекает из рис. 2.14,
а, может быть построена по характеристике нелинейного источника путем параллельного переноса оси тока в точку холостого хода с последующим опрокидыванием кривой относительно новой оси (рис. 2.14, б). При этом, как видно из сопоставления углов и на рис. 2.14, а и б, введенные ранее понятия статического и дифференциального внутренних сопротивлений источника совпадут с понятиями статического
RСТ.И UIИ k t g
и дифференциального
RИd ddUIИ k t g
сопротивлений нелинейного резистора RИ , отражающего в эквивалентной схе-
ме роль внутреннего сопротивления источника.
Расширенная область характеристик источников. Обратим внимание,
что все источники, как линейные, так и нелинейные являются примерами не-
симметричных элементов электрической цепи, поскольку их характеристики несимметричны относительно начала координат. До сих пор мы не рассматривали характеристик источников в области отрицательных токов, то есть токов, направленных навстречу действию источников. Однако в ряде задач, например при расчетах сложных нелинейных цепей, с этой областью характеристик источников приходится встречаться, ибо в таких цепях отдельные источники могут оказаться в режиме, при котором токи в них под действием остальной части цепи будут протекать навстречу действию этих источников.
На рис. 2.15, а показаны характеристики линейного 1 и нелинейного 2 источников в расширенной области, включая также область при токах больше тока I K короткого замыкания, в которую может перейти режим работы источни-
ка под воздействием других источников цепи. Соответствующие характеристики резисторов, отражающих внутренние сопротивления этих источников, приведены на рис. 2.15, б.
2.3. Графический метод расчёта простых нелинейных цепей
Графический метод. Простейшим приемом расчета нелинейных цепей является графический метод, опирающийся на графическое изображение вольтамперных характеристик элементов цепи.
а)
б)
Рис. 2.15. Характеристики линейного 1 и нелинейного 2 источников При непосредственном соединении нелинейных источника и приемника
для нахождения режима их совместной работы достаточно на одном графике совместить внешнюю характеристику И источника и вольт-амперную характе-
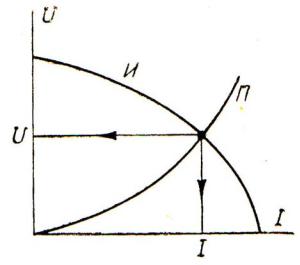
ристику П приемника (см. рис. 2.16). Точка пересечения этих характеристик определит напряжение U и ток I рассматриваемой цепи.
Рис. 2.16. Простейшая электрическая цепь: работа нелинейного источника на нелинейный приёмник
Переходя к расчету простых нелинейных цепей с несколькими приемниками, остановимся только на случае их питания от идеального источника напряжения, так как при неидеальном, и в частности нелинейном источнике, имеется возможность представить такой источник в виде последовательного соединения идеального источника напряжения и нелинейного резистора. Относя резистор к группе приемников, приходим к упомянутой упрощенной формулировке задачи.
Последовательное соединение. Порядок расчета цепи, состоящей из последовательного соединения нелинейных приёмников (на рис. 2.17 для определенности приведена схема цепи с тремя приемниками, один из которых взят линейным), зависит от постановки задачи, в частности от того, является ли заданным ток I в цепи и требуется ли найти суммарное напряжение U, или, наоборот, задано напряжение на всей цепи, а ее ток является предметом расчета.
В первом случае, то есть при заданном токе I , являющемся общим для всех включенных приемников, по заданным характеристикам последних (рис. 2.18) определяют напряжения U1,U2 ,U3 на каждом из приемников и, складывая их, получают искомый результат:
U U1 U2 U3 .
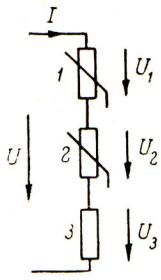
Рис. 2.17. Последовательная цепь с одним линейным и двумя |
нели- |
нейными приёмниками |
|
В случае, когда задано напряжение U на всей цепи, непосредственно использовать характеристики отдельных приемников не представляется возможным, так как не известны ни ток, ни напряжения U1,U2 ,U3 отдельных прием-
ников. Здесь приходится обращаться к понятию эквивалентного нелинейного приемника, заменяющего группу из последовательно соединенных приемников, и строить его эквивалентную вольт-амперную характеристику. Очевидно, напряжение на эквивалентном приемнике при любом токе должно равняться сумме напряжений на каждом из отдельных приемников при том же токе. Поэтому для построения характеристики эквивалентного приемника достаточно, задавшись произвольным рядом токов, несколько раз решить предыдущую задачу (для каждого из выбранных токов) и получить соответствующий ряд суммарных напряжений.
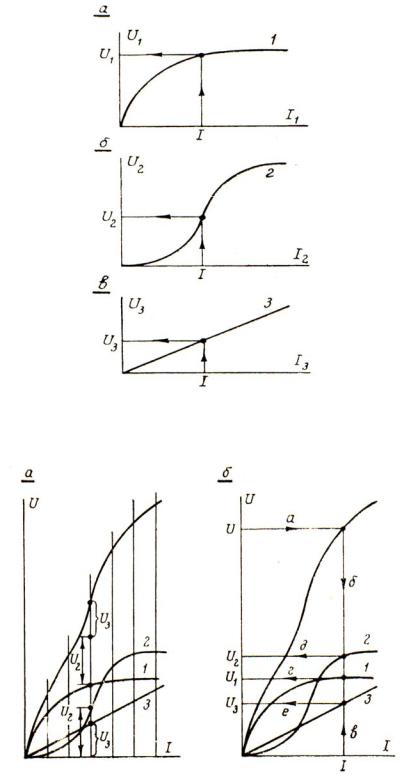
Рис. 2.18. Вольт-амперные характеристики элементов |
после- |
довательной цепи |
|
Рис. 2.19. Суммарная вольт-амперная характеристика |
по- |
следовательной цепи |
|
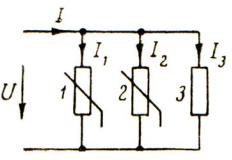
Подобную операцию проще всего можно выполнить графически, совмещая характеристики отдельных приемников на одном чертеже и складывая ординаты кривых при нескольких произвольно выбранных токах, как показано на рис. 2.19, а. Очевидно, чем плотнее ряд выбранных токов, тем точнее будет построение характеристики эквивалентного приемника. Условимся в дальнейшем называть рассмотренную операцию суммированием характеристик.
Располагая полученным графиком (на рис. 2.19, б он повторен без вспомогательных построений), можно для любого заданного напряжения U по характеристике эквивалентного приемника найти ток I в цепи (операция а – б), после чего, используя характеристики отдельных приемников, определить напряжения U1,U2 ,U3 на этих приемниках (операции в– г, в – д и в – е).
Параллельное соединение. При параллельном соединении нелинейных приемников (рис. 2.20) проще решается задача по определению токов I1, I2 , I3
приемников по заданному напряжению U на зажимах цепи. Являясь общим для всех приемников, оно позволяет по заданным характеристикам приемников найти их токи (рис. 2.21), суммируя которые нетрудно рассчитать ток в неразветвленной части цепи:
I I1 I2 I3 .
Рис. 2.20. Параллельное соединение приёмников
В случае, если заданной величиной в цепи будет суммарный ток I , а требуется определить приложенное к цепи напряжение U и токи I1, I2 , I3 каждого
приемника, необходимо прибегать к понятию эквивалентного нелинейного приемника, заменяющего группу из отдельных параллельно соединенных приёмников.
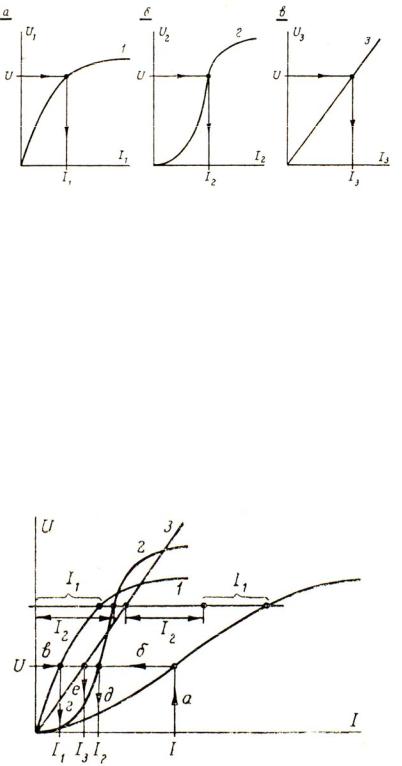
Рис. 2.21. Вольт-амперные характеристики элементов параллельной цепи
Поскольку ток эквивалентного приемника при любом напряжении должен равняться сумме токов отдельных приемников при том же напряжении, то для построения вольт-амперной характеристики эквивалентного приемника необходимо осуществить суммирование характеристик отдельных приемников, но не в направлении оси напряжения, как это делалось выше, а в направлении оси тока, как показано на рис. 2.22. Выполненные построения позволяют для любого заданного тока I по характеристике эквивалентного приемника найти питающее цепь напряжение U (операция а – б), после чего, используя характеристики отдельных приемников, определить их токи I1 , I 2 , I3 (операции в–г, в–д
и в–е).
Рис. 2.22. Суммарная вольт-амперная характеристика параллельной цепи
Смешанное соединение. Владея приемами расчета нелинейных цепей при последовательном и параллельном соединениях приемников, можно решить и более сложные задачи расчета цепей при смешанном соединении приемников.
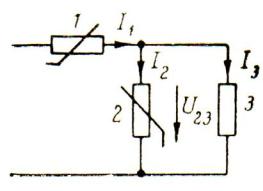
При этом обратные задачи, связанные с нахождением напряжения на всей цепи по заданному току в наиболее отдаленном от источника приемнике, решаются непосредственно по характеристикам отдельных приемников без ка- ких-либо дополнительных построений.
Рис. 2.23. Смешанное соединение приёмников
Например, для цепи, показанной на рис. 2.23, при заданном токе I3
третьего приемника, прежде всего по его характеристике (см. рис. 2.21), находят напряжение на третьем приемнике. Так как это напряжение в силу параллельного соединения второго и третьего приемников является одновременно и напряжением на втором приемнике, то, воспользовавшись его характеристикой, определяют ток I2 второго приемника, который в сумме с третьим током I3
даст ток I1 первого приемника. По последней величине с помощью характери-
стики первого приемника находят напряжение на (первом приемнике, складывая с которым напряжение на третьем приемнике, получают искомое напряжение U цепи.
Для решения прямых задач, в которых заданной величиной является напряжение на всей цепи, приходится прибегать к 'построению эквивалентных характеристик различных групп приемников. В только что рассмотренном примере цепи (рис. 2.23) при заданном питающем напряжении U необходимо прежде всего построить эквивалентную вольт-амперную характеристику 23 (рис. 2.24) группы параллельно соединенных второго и третьего приемников, для чего следует суммировать их характеристики 2 и 3 в направлении оси токов.
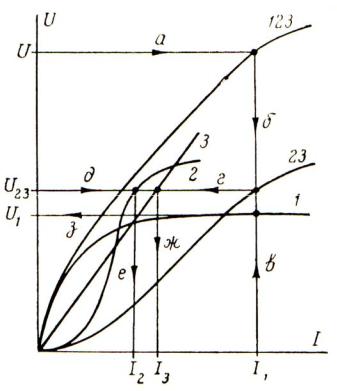
Рис. 2.24. Суммарная вольт-амперная характеристика смешанной цепи
Теперь возможно построение эквивалентной характеристики 123 всей цепи в целом. Для этого, принимая во внимание последовательное соединение группы 23 с первым приемником, необходимо суммировать характеристику 23 с характеристикой 1 первого приемника в направлении оси напряжений.
Полученная эквивалентная характеристика позволяет при заданном напряжении U на всей цепи найти ток в ее неразветвленной части (операция а–б). Так как упомянутый ток одновременно является током группы второго и третьего приемников, то, воспользовавшись эквивалентной характеристикой 23, получаем возможность по току I1 I23 определить напряжение U23 на этой
группе (операция в–г). Последнее с помощью характеристик 2 и 3 второго и третьего приемников позволяет получить их токи I2 и I3 (операции д–е и д–
ж). Напряжение U1 на первом приемнике в случае необходимости может быть найдено по характеристике 1 и току I1 (операция в–з).
Возможности графического расчета. Рассмотренные приемы позволя-
ют осуществить расчет любой простой цепи, но при громоздкой ее конфигурации графические построения будут выглядеть довольно запутанно.
2.4. Графический метод расчёта ограниченно сложных |
нели- |
нейных цепей |
|
Рассмотренные в предыдущем параграфе приемы расчета простых нелинейных цепей можно использовать и для расчета ограниченно сложных цепей, образованных смешанным (последовательно-параллельным) соединением ветвей, если ввести понятие о вольт-амперной характеристике ветви, представляющей зависимость напряжения между концами ветви от протекающего по ней тока. В этом случае каждая ветвь будет выступать как один нелинейный элемент, а вся цепь будет представлять собой смешанное соединение таких элементов.
Вольт-амперная характеристика ветви может быть построена, если известны характеристики всех входящих в нее элементов, причем последние в общем случае должны быть заданы для двух направлений токов. Это объясняется тем, что при расчете сложных цепей, и в частности ограниченно сложных, мы не можем заранее предвидеть направления токов в ветвях, и поэтому построение вольт-амперных характеристик ветвей приходится выполнять как для области положительных, так и для области отрицательных токов. При этом в случае несимметричных элементов следует позаботиться о строгом согласовании их положительных токов на вольт-амперных характеристиках и в схеме цепи, с тем чтобы в положительном направлении оси тока располагалась именно та ветвь характеристики данного нелинейного элемента, которая соответствует выбранному положительному направлению тока через рассматриваемый элемент в цепи.
Рассмотрим построение вольт-амперной характеристики для простейшего случая, когда в ветвь между узлами k и m (рис. 2.25) входят один идеальный источник напряжения с ЭДС Ekm , действующей от узла k к узлу m , и один не-
линейный приемник, представленный своей вольт-амперной характеристикой (кривая П на рис. 2.26). Зададимся положительным направлением тока Ikm в ветви, совпадающим с направлением ЭДС источника, и аналогичным направлением напряжения Ukm между ее концами.
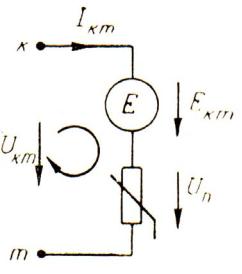
Рис. 2.25. Ветвь цепи между узлами k и m
На основании второго закона Кирхгофа, записанного для контура, проходящего через рассматриваемую ветвь (см. рис. 2.25), имеем
Ukm U П Ekm ,
откуда следует, что для построения вольт-амперной характеристики ветви Ukm f Ikm необходимо из характеристики приемника вычесть в направлении
оси напряжение ЭДС источника. Поскольку последняя величина является постоянной, указанное действие эквивалентно переносу характеристики приемника параллельно самой себе вниз на расстояние, соответствующее (в масштабе напряжений) ЭДС Ekm источника, как показано на рис. 2.26.
Нетрудно убедиться, что к рассмотренному простейшему случаю легко приводится любая задача о построении характеристики ветви, содержащей произвольное количество нелинейных источников и приемников. Действительно, каждый из нелинейных источников может быть представлен как последовательное соединение идеального источника напряжения и нелинейного резистора. В свою очередь, все идеальные источники напряжения легко объединяются в один источник, а все нелинейные резисторы с нелинейными приемниками ветви можно заменить одним эквивалентным нелинейным приемником.
Однако при небольшом количестве источников в ветви прибегать к их расчленению на идеальные источики и нелинейные резисторы нецелесообразно. В этом случае при построении вольт-амперной характеристики ветви проще использовать исходные внешние характеристики нелинейных источников, как это проделано в следующем пункте на частном примере расчета цепи.
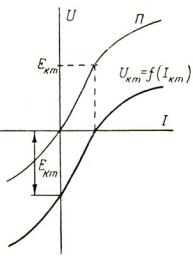
Рис. 2.26. Вольт-амперная характеристика ветви k m
Пример расчета. Графический расчет ограниченно сложных нелинейных цепей на основе характеристик их ветвей рассмотрим для цепи, приведенной на рис. 2.27, а и соответствующей параллельной работе двух источников И1 и И2 через линии передачи Л1 и Л2 на общий приемник П. При этом нелинейными будем считать только источник И2 и приемник П, полагая остальные элементы цепи линейными. Пусть линейный источник И1 задан его ЭДС E1 и внутрен-
ним сопротивлением RИ1, линии передачи определены их сопротивлениями RЛ1 и RЛ2 , а для нелинейных элементов представлены вольт-амперные харак-
теристики И2 и П (рис. 2.27).
Построим характеристики первой и второй ветвей, включающих источники И1 и И2, задавшись направлениями токов I1 и I2 в них и напряжением
U12 между узлами 1 и 2 так, как это показано на рис. 2.27, а. Представив первую ветвь в виде эквивалентного линейного источника с ЭДС E1 и внутренним сопротивлением RИ1 RЛ1 , ее характеристику 1 (см. рис. 2.28) построим но уравнению
U E1 (RИ1 RЛ1) I .
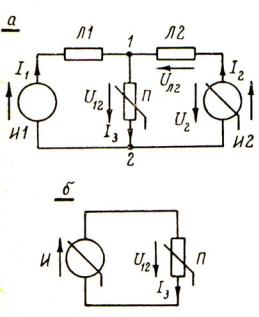
Рис. 2.27. Ограниченно сложная нелинейная цепь
Для построения характеристики второй ветви выберем на схеме рис. 2.27, а в соответствии с обычными правилами направления напряжений U2 на ис-
точнике И2 и U Л2 на линии Л2 и составим уравнение по второму закону Кирхгофа для правого контура схемы. Из этого уравнения получим
U12 U2 U Л2 ,
откуда следует, что для построения характеристики 2 второй ветви необходимо из заданной характеристики источника И2 (рис. 2.28) вычесть в направлении оси напряжения характеристику линии Л2, которую нетрудно предварительно построить по уравнению
U RЛ2 I .
Рассматривая далее первую и вторую ветви как параллельно соединенные эквивалентные источники, объединим их в один эквивалентный источник (рис. 2.27, б), характеристику И которого (рис. 2.28) можно найти суммированием характеристик 1 и 2 первой и второй ветвей в направлении оси тока, поскольку ток нового эквивалентного источника равен сумме токов первой и второй ветвей:
I3 I1 I2 .

Рис. 2.28. Вольт-амперные характеристики источника И2 и приёмника П
Представление двух ветвей в виде одного эквивалентного источника И привело исходную схему к схеме непосредственного соединения этого источника с приемником П (рис. 2.27, б), режим в которой определяется точкой k пересечения характеристик упомянутых элементов (рис. 2.28). Таким образом, находим ток I3 приемника (операция а) и напряжение U12 между узлами цепи
(операция б), которое в свою очередь позволяет с помощью характеристик 1 и 2 первой и второй ветвей получить токи I1 и I2 (операции в–г и д–е).
RСТ
RСТ
Рис. 2.29. Суммарная вольт-амперная характеристика ограниченно сложной цепи
Отрицательное значение тока I2 свидетельствует, что в рассмотренном
примере ток во второй ветви течет навстречу первоначально выбранному нами направлению, то есть против направления действия второго источника.
Об отрицательном интегральном сопротивлении. Вольт-мперная ха-
рактеристика ветви, содержащей источники, например характеристику Ukm f Ikm , построенная на рис. 2.27, не проходит через начало координат,
что обязывает рассматривать такую ветвь как некоторый эквивалентный источник. Если же к ветви формально подходить как к эквивалентному приемнику, что иногда практикуется, то в этом случае приходится столкнуться с понятием отрицательного статического сопротивления
RСТ UI 0 ,
которое имеет место на участке аб характеристики (рис. 2.29), где положительному току I соответствует отрицательное напряжение U.
С отрицательным сопротивлением двухполюсника можно встретиться и в линейных цепях, если, несмотря на имеющиеся внутри него источники, формально будем считать этот двухполюсник приемником.
2.5. Расчёт сложной цепи с одним нелинейным элементом
Если в сложной цепи присутствует только один нелинейный элемент, то ее расчет не представляет существенных затруднений и может быть выполнен на основе метода эквивалентного источника.
Пусть в некоторой сложной цепи (рис. 2.30, а) таким единственным нелинейным элементом будет приемник П. Представив всю остальную цепь по отношению к нему в виде эквивалентного источника, приходим к эквивалентной схеме непосредственного соединения источника с нелинейным приемником (рис. 2.30, б). При этом эквивалентный источник является линейным элементом, так как часть сложной цепи, которую заменили эквивалентным источником (рис. 2.30, в), не содержит нелинейных элементов.
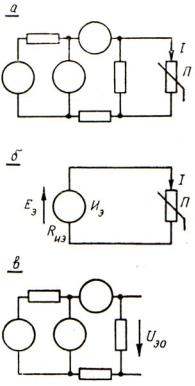
Рис. 2.30. Сложная цепь с нелинейным элементом
Таким образом, расчет эквивалентных параметров такого источника, в частности ЭДС EЭ , равной напряжению U Э0 на разомкнутой ветви нелинейного
приемника, и внутреннего сопротивления RИ Э , представляющего сопротивле-
ние цепи относительно точек разрыва этой ветви, может быть выполнен по правилам, изложенным при описании метода эквивалентного источника для расчета линейных цепей. Определение же режима в цепи при непосредственном соединении линейного источника и нелинейного приемника элементарно осуществляется графическим путем, изложенным в п. 2.3.
После нахождения тока I и напряжения U на нелинейном приемнике последний можно заменить линейным приемником с сопротивлением R U / I и для определения остальных токов цепи продолжить расчет уже целиком линейной цепи.
Рассмотренный прием расчета сложной нелинейной цепи можно распространить и на цепь с несколькими нелинейными приемниками, если только они образуют одну простую группу, соединенную с остальной линейной частью цепи двумя зажимами. Заменив тогда указанную группу приемников одним эквивалентным нелинейным приемником, сведем более сложную задачу к только что рассмотренному варианту. К нему приводится и задача, в которой единственным нелинейным элементом сложной цепи будет источник, так как согласно
изложенному выше (п. 2.3) всякий нелинейный источник можно заменить совокупностью идеального источника и нелинейного резистора.
2.6. Аналитические методы расчёта и исследования нелинейных цепей
Рассмотренные в предыдущих параграфах графические методы расчета нелинейных цепей весьма наглядны и достаточно просты, но страдают, как и всякие графические методы, ограниченной точностью расчета. Кроме того, они вообще не допускают проведения общего анализа закономерностей в электрических цепях. Поэтому в ряде случаев приходится прибегать к аналитическим методам расчета и анализа нелинейных цепей.
Эти методы основаны на выражении вольт-амперных характеристик нелинейных элементов в виде аналитических зависимостей
Uk f Ik
с последующей их подстановкой в уравнения, записанные для исследуемой цепи по методу токов в ветвях, в частности в уравнения, составленные по второму закону Кирхгофа:
Uk |
En |
k |
n |
для системы независимых контуров цепи. |
|
Успех решения такой задачи определяется, с одной стороны, точностью, с которой удастся подобрать аналитическую функцию Uk f Ik , изображаю-
щую заданную (обычно графически или в виде таблицы) вольт-амперную характеристику того или иного нелинейного элемента, а с другой стороны, — простотой подобранной аналитической функции с точки зрения возможности последующего решения полученной системы уравнений. Необходимость удовлетворения двум указанным, как правило, противоречивым требованиям делает задачу о подборе аналитической зависимости для вольт-амперных характеристик одним из самых ответственных этапов аналитического расчета нелинейной цепи, а невозможность предложить в этом направлении каких-либо стандартных решений требует от расчетчиков большого искусства и изобретательности.
Линейная аппроксимация. Как известно из курса математики, любая непрерывная функция может быть разложена в ряд Маклорена, то есть представлена степенным полиномом, который применительно к вольт-амперной характеристике будет выглядеть в виде
U a0 a1I a2 I 2 ... an I n ,
Причем, чем больше членов будет взято в этом полиноме, тем ближе окажется аналитическая аппроксимация к исходной вольт-амперной характеристике. Однако с увеличением числа членов полинома возрастает порядок уравнений, описывающих процессы в данной электрической цепи, и соответственно затрудняется задача решения такой системы уравнений. Поэтому при инженерных расчетах практически не пользуются полиномами со степенью выше третьей и по возможности предпочитают ограничиваться лишь первыми двумя членами разложения, прибегая к линейной аппроксимации вольт-амперных характеристик. Несмотря на кажущуюся на первый взгляд неприемлемость замены при сколь-нибудь ответственных расчетах криволинейной характеристики прямой линией, такая аппроксимация позволяет получить решение нелинейной задачи с высокой степенью точности. Это объясняется тем, что в большинстве практических случаев бывает известна область вольт-амперной характеристики, в пределах которой ожидается работа того или иного нелинейного элемента. В ограниченной же области нелинейной характеристики линейная аппроксимация может дать весьма высокое совпадение с действительной кривой. Так, например, вольт-амперная характеристика варистора, представленная на рис. 2.31, с высокой степенью точности заменяется прямой 1 на начальном участке Оа или прямой 2 на последнем участке вг.
При этом в первом случае уравнение прямой приобретает простейший
вид:
U a1I RСТ I ,
где RСТ k tg α — среднее статическое сопротивление варистора на участке 0 – а, а во втором случае уравнение прямой записывается в форме
U a0 a1I U H Rd I ,
где U H — напряжение, соответствующее отрезку, отсекаемому на оси ординат прямой 2 (начальное напряжение), a Rd k tg β — среднее дифференциальное сопротивление варистора на участке вг.
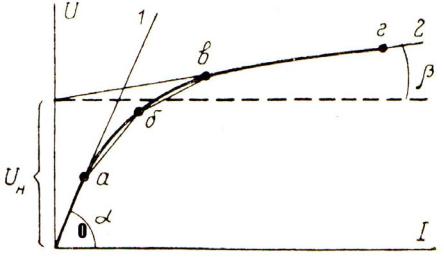
Рис. 2.31. Вольт-амперная характеристика варистора
При этом в первом случае уравнение прямой приобретает простейший
вид:
U a1I RСТ I ,
где RСТ k tg α — среднее статическое сопротивление варистора на участке 0– а, а во втором случае уравнение прямой записывается в форме
U a0 a1I U H Rd I ,
где U H — напряжение, соответствующее отрезку, отсекаемому на оси ординат прямой 2 (начальное напряжение), a Rd k tg β — среднее дифференциальное
сопротивление варистора на участке вг.
На резко закругленном участке ав спрямление характеристики приводит к большим погрешностям, однако они также могут быть сведены до желаемого минимума дроблением этого участка на более мелкие части (на рис. 2.31 участок ав подразделен на две части – аб и бв).
Замена большого участка нелинейной характеристики ломаной линией, как это сделано на рис. 2.31, получила название кусочно-линейной аппроксимации. К ней широко прибегают при анализе работы нелинейных цепей при изменяющихся токах, причем по мере перехода режима из одной области характеристики в другую сменяют и уравнение аппроксимирующей прямой. При расчете же определенного режима в цепях постоянного тока вполне достаточно ограничиться спрямлением характеристики на каком-либо одном участке.
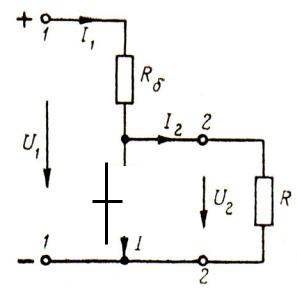
Аналитическое исследование работы диодного стабилизатора на-
пряжения. В качестве примера использования линейной аппроксимации рассмотрим анализ работы газоразрядного стабилизатора напряжения.
Стабилизатором напряжения называют промежуточное устройство, включаемое между источником и приемником и предназначенное для поддержания на приемнике неизменного значения напряжения при возможных колебаниях напряжения источника. Обычно стабилизаторы применяются для поддержания постоянного напряжения на ответственных приемниках при их питании от общих сетей, напряжение которых обычно претерпевает некоторые изменения.
Стабилизатор, схема которого вместе с присоединенным к нему приемником R приведена на рис. 2.32, состоит из линейного балластного резистора Rб и стабилитрона VD. Напряжение U1 сети подается на входные зажимы 1-1
стабилизатора, а приемник R присоединяется к его выходным зажимам 2-2.
VD
Рис. 2.32. Схема стабилизатора
Стабилитрон является полупроводниковым прибором, обратную вольтамперную характеристику которого можно представить в виде, показанном на рис. 2.33. Поскольку стабилитрон нормально работает на обратном участке своей характеристики, при исследовании работы стабилизатора достаточно аналитически выразить только этот практически прямой ее участок. Прямая ветвь стабилитрона аналогична прямой характеристике диода и не используется для стабилизации напряжения.
Рис. 2.33. Вольт-амперная характеристика стабилитрона
Используя приведенные на рис. 2.32 обозначения токов и напряжений, уравнение прямой, отвечающей участку аб характеристики стабилитрона, можно записать в виде
1) U2 U H Rd I ,
где U H — напряжение, соответствующее отрезку, отсекаемому прямой аб на оси ординат (рис. 2.34); Rd — дифференциальное сопротивление стабилитрона
на этом участке его характеристики.
Составляя для цепи стабилизатора (рис. 2.32) очевидные уравнения
2)I1 I I2 ;
3)U1 RбI1 U2 ;
4)U2 R I2
иприсоединяя к ним ранее записанное уравнение характеристики стабилитро-
на, получаем систему из четырех линейных уравнений, в которых при заданном
питающем напряжении U1 и известных |
параметрах элементов цепи |
U H , Rd , Rб , R четыре величины – I1, I, I2 и U2 |
являются искомыми. |
Не ставя задачи конкретно рассчитать режим стабилизатора при опреде- |
|
ленном питающем напряжении, постараемся на основании полученных уравнений найти общую связь между входным и выходным напряжениями стабилизатора. Для этого из последних двух уравнений определим токи:
I |
U1 U2 ; |
I |
2 |
U2 |
1 |
Rб |
|
R |
|
|
|
|
и с их помощью из второго уравнения определим ток стабилитрона:

I I1 I2 U1 U2 U2 .
Rб Rб R
Подставляя этот результат в уравнение характеристики стабилитрона, имеем
U2 U H Rd U1 Rd U2 Rd U2 , Rб Rб R
откуда для U 2 получим
U H Rd U1
U2 1 Rd Rб Rd .
Rб R
Так как задачей стабилизатора является поддержание постоянства выходного напряжения U2 при возможных изменениях входного напряжения U1 , то для идеальной работы стабилизатора необходимо отсутствие какой-либо зависимости напряжения U2 от напряжения U1 . Из полученного выражения для напряжения U2 вытекает, что оно не будет зависеть от входного напряжения U1 в единственном случае, если коэффициент Rd / Rб при U1 обратится в нуль, то есть когда дифференциальное сопротивление Rd стабилитрона будет равно ну-
лю.
Таким образом, идеальная работа стабилизатора возможна лишь при строгой горизонтальности линейного участка характеристики стабилитрона, а качество работы реального стабилизатора будет тем выше, чем меньше дифференциальное сопротивление стабилитрона на рабочем участке его характеристики.
Метод последовательных приближений. В тех случаях, когда при рас-
чете нелинейных цепей нельзя заранее предвидеть область работы того или иного нелинейного элемента цепи, возможность линейной аппроксимации характеристик не исключена и к ней прибегают в совокупности с методом последовательных приближений.
Идея метода в применении к цепи с одним нелинейным элементом заключается в том, что, приступая к расчету цепи, сначала спрямляют характеристику нелинейного элемента на весьма большом ее участке (прямая I на рис. 2.34). Записав уравнение прямой при таком весьма грубом приближении, рассчитывают цепь и определяют в качестве первого приближения ток I в нели-
нейном элементе. По полученному результату делают заключение о приблизительной области на характеристике нелинейного элемента, в пределах которой можно ожидать работу этого элемента, и в качестве второго приближения спрямляют характеристику на более узком участке в окрестности первого решения I (прямая 2). Составив уравнение такой прямой, вновь решают задачу и находят новое значение I тока в нелинейном элементе, которое, являясь более точным решением, позволяет еще сузить область ожидаемого режима нелинейного элемента и тем самым осуществить следующую стадию уточнения линейной аппроксимации характеристики нелинейного элемента (прямая 3). Так, повторяя расчеты, можно достичь любой степени точности решения задачи.
Важно только, чтобы каждый последующий ответ для тока нелинейного элемента укладывался в предлагаемую для него на основании предыдущего решения область спрямленной характеристики. Это обстоятельство заставляет соблюдать умеренность в стремлении возможно скорее сузить область спрямления характеристики, особенно при сложной форме вольт-амперной характеристики нелинейного элемента.
Рис. 2.34. Вольт-амперная характеристика нелинейного элемента
Указанный прием пригоден для расчета цепи и с несколькими нелинейными элементами, однако процесс сходимости результатов последовательных расчетов к истинному режиму будет протекать медленнее и для получения ответа желаемой точности придется выполнить большее число последовательных приближений.
2.7. Вопросы устойчивости режима в нелинейных цепях
Все рассмотренные выше задачи анализа электрических цепей приводят к заключению, что режим в цепи вполне однозначно определяется заданными па-

раметрами и характеристиками ее элементов и при неизменности этих параметров и характеристик также будет оставаться без изменения. Однозначность и стационарность режима в электрических цепях при заданных неизменных параметрах и характеристиках входящих в них элементов, действительно, имеют место во всех линейных цепях и большинстве нелинейных. Однако в некоторых нелинейных цепях в случае, когда в них присутствуют элементы с падающими участками вольт-амперных характеристик, возможно установление не одного, а нескольких, отличных друг от друга, режимов. Иногда же в таких цепях стационарные режимы, то есть режимы с неизменяющимися токами, вообще неосуществимы. Иначе говоря, ток в таких цепях даже теоретически никогда не может принять постоянного значения.
Условие неизменности тока в цепи. Перед тем как подробнее познако-
миться с упомянутыми выше своеобразными явлениями, расширим наши представления об условиях неизменности тока в электрической цепи.
Рассматривая простейший случай передачи энергии от источника к приемнику по соединительной линии, мы не учитывали ее индуктивности. Это было вполне оправданно, так как изучавшиеся режимы характеризовались постоянством тока в цепи, при котором индуктивность линии не может оказать на режим какого-либо влияния. Сейчас, когда мы переходим к выяснению условий неизменности режима в электрической цепи, то есть когда мы неизбежно столкнемся с процессами при изменяющихся токах, пренебрежение индуктивностью соединительных проводов недопустимо. При изменяющихся токах в проводах будут индуктироваться ЭДС индукции, определяющиеся согласно закону электромагнитной индукции скоростью изменения тока во времени:
EL L dd It ,
где L — индуктивность соединительных проводов.
Поэтому, обращаясь к упомянутому случаю передачи энергии от источника И к приемнику П по линии (рис. 2.35) и пренебрегая для упрощения картины сопротивлением этой линии, на основании второго закона Кирхгофа для контура цепи можем написать:
U П U EL
или с учетом приведенного выше выражения для ЭДС EL , индуктирующейся в проводах линии,
U U П L dd It .
Признаком постоянства тока в цепи является равенство нулю его производной d I / d t , которое, как следует из полученного уравнения, будет иметь
место при равенстве напряжений U источника и U П приемника.
Если же напряжение источника окажется больше напряжения приемника (U U П ), то разность в левой части последнего уравнения будет иметь положительный знак. Положительной, следовательно, будет и производная d I / d t (индуктивность L всегда положительна), означая тем самым, что ток I в цепи будет увеличиваться.
Рис. 2.35. Схема передачи электроэнергии
В случае преобладания напряжения приемника над напряжением источника {U П U ) производная от тока по времени окажется отрицательной, что
будет свидетельствовать об уменьшении тока в цепи. Сделанные выводы об условиях неизменности, возрастания или убывания тока в 'простейшей цепи являются исключительно важными при оценке поведения электрических цепей в тех или иных случаях и будут нами широко использованы при дальнейшем изложении этого параграфа.
Устойчивое и неустойчивое равновесия. Упомянутое выше равенство напряжений U П приемника и U источника, выражающее точное соответствие
ответной реакции приемника на (приложенное к нему внешнее воздействие и потому называемое условием равновесия в цепи, является необходимым условием для неизменности тока в цепи, но оказывается недостаточным условием для стационарности режима, под которой понимают практическую способность работы цепи при постоянном токе. Как и во всякой механической системе, в электрической цепи стационарный режим обеспечивается лишь устойчивым равновесием. Неустойчивое равновесие не обеспечивает в цепи стационарного
режима и, как правило, делает этот режим практически вообще неосуществимым.
Понятия устойчивости и неустойчивости равновесия проще всего усвоить на примере простой механической системы, например шарика, находящегося на твердой поверхности. На рис. 2.36 показаны шарики, лежащие на вогнутой и выпуклой поверхностях и находящиеся в состоянии равновесия, когда сила тяжести fG шариков в точности уравновешивается силой fQ реакции поверхно-
сти. Очевидно существенное различие равновесий в этих двух случаях, первый из которых (рис. 2.36, а) относится к случаю устойчивого равновесия, а второй (рис. 2.36, б) является примером неустойчивого равновесия.
Если шарик, лежащий в низине вогнутой поверхности, вывести из состояния равновесия, сдвинув его немного в сторону, то возникающая в этом случае результирующая сила будет стремиться вернуть шарик в исходное положение. В случае же шарика, лежащего на вершине выпуклой поверхности, малейшее отклонение его от состояния равновесия вызовет силу, стремящуюся увести шарик еще дальше от состояния равновесия.
Рис. 2.36. Системы устойчивого и неустойчивого равновесия
Упомянутыми различиями в поведении системы при отклонении ее от состояния равновесия и пользуются при выяснении устойчивости или неустойчивости данного равновесия. Осуществляя небольшое искусственное отклонение системы от равновесия, проводят анализ ее дальнейшего поведения. Если система стремится вернуться к состоянию равновесия, то это означает, что данное равновесие является устойчивьш. Если же при малом отклонении от равновесия
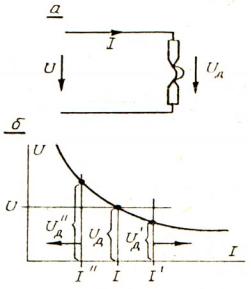
в системе возникают силы, еще дальше уводящие ее от равновесия, то, следовательно, здесь имеет место неустойчивое равновесие.
Указанный прием может быть использован как в условиях механических систем, так и в применении к процессам в электрических цепях.
Невозможность длительного горения электрической дуги при пита-
нии от постоянного напряжения. В качестве примера неустойчивого равновесия в электрической цепи рассмотрим горение электрической дуга при ее питании непосредственно от источника с неизменным напряжением, например от мощной сети (рис. 2.37, а).
Особенностью электрической дуги является ее падающая вольт-амперная характеристика, приведенная на рис. 2.37, б. При заданном напряжении источника U ток, соответствующий равновесию в цепи, нетрудно найти, проводя горизонталь из точки на оси напряжений, соответствующей заданному напряжению, до пересечения с характеристикой дуги. Действительно, именно при этом токе I напряжение U Д на дуге в точности равно напряжению U источника.
Рис. 2.37. Схема электрической дуги
Убедимся, однако, в том, что найденный режим соответствует неустойчивому равновесию в цепи и поэтому практически существовать не может. Если вывести режим цепи из равновесия, например, в сторону увеличения тока до значения I , то напряжение на дуге уменьшится и примет новое значение U Д .
При этом равновесие напряжений нарушится в сторону преобладания питающего напряжения, что повлечет за собой, как было установлено ранее, увеличение тока, то есть дальнейшее отклонение режима от равновесия. Характерно, что рассматриваемый процесс будет развиваться лавинообразно, так как при
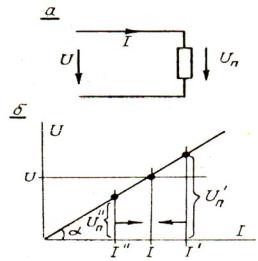
дальнейшем. увеличении тока разность U U Д питающего напряжения и на-
пряжения на дуге, будет возрастать, вызывая более стремительное возрастание тока.
Наоборот, предположив, что мы вывели режим цепи из равновесия в сторону уменьшения тока, например до его значения I , нетрудно убедиться, что на этот раз напряжение U Д на дуге станет выше напряжения U источника, что
вызовет дальнейшее уменьшение тока, то есть опять-таки увеличение отклонения режима в цепи от равновесия.
Таким образом, стационарный режим горения дуги при ее непосредственном питании от источника с неизменным напряжением невозможен, ибо, если даже и удастся в начале достигнуть условия равновесия, то оно под воздействием случайных причин неизбежно будет нарушено или в сторону теоретически неограниченного возрастания тока (практически это приведет к аварии), или в сторону убывания тока в цепи до нуля, когда дуга полностью погаснет.
Рис. 2.38. Устойчивость горения дуги при линейном приёмнике
Анализ устойчивости режима при линейном приемнике. В свете ска-
занного интересно проанализировать устойчивость режима в аналогичных условиях (рис. 2.38, а), но, когда приемник обладает обычной, возрастающей характеристикой, например линейной, как показано на рис. 2.38, б, выведя режим цепи из равновесия в сторону увеличения тока, убеждаемся, что напряжение U П на приемнике становится больше напряжения U источника, в результате
чего будет наблюдаться уменьшение тока, то есть возвращение режима к равновесию. Если мысленно уменьшить ток в цепи против его равновесного значения, то напряжение U П на приемнике, наоборот, упадет и преобладающее
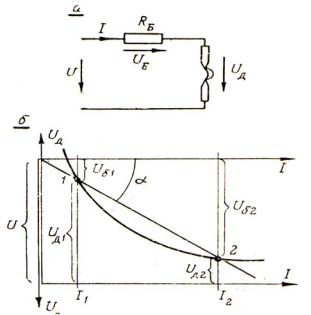
напряжение U источника вызовет увеличение тока, то есть опять-таки возвращение процесса в цепи к равновесному режиму. Вот поэтому определяемый по графику на рис. 2.38, б ток I будет устойчиво существовать в такой цепи до тех пор, пока не изменятся параметры цепи.
Устойчивый режим горения дуги можно получить включением последовательно с ней балластного резистора Rб (рис. 2.39, а). В этом случае под на-
пряжением приемника следует понимать сумму напряжений Uб на балластном резисторе и U Д на дуге. Тогда условие равновесия в цепи выразится равенст-
вом
U Uб U Д .
Рис. 2.39. Схема с последовательно включённым балластным резистором
Для определения режима, соответствующего этому условию, удобно воспользоваться построением, показанным на рис. 2.39, б и представляющим собой совмещение падающей характеристики дуги с линейной характеристикой балластного резистора, причем последняя опрокинута вокруг оси тока и наложена на характеристику дуги так, чтобы оси напряжений обеих характеристик совпадали, а оси токов размещались на расстоянии, равном напряжению U источника питания. Нетрудно убедиться, что точки 1 и 2 пересечения обеих характеристик как раз определяют режимы, соответствующие сформулированному выше условию равновесия в цепи, так как именно в этих точках сумма отрезков, изображающих напряжение на резисторе и дуге, в точности равна отрезку, изображающему напряжение источника питания.
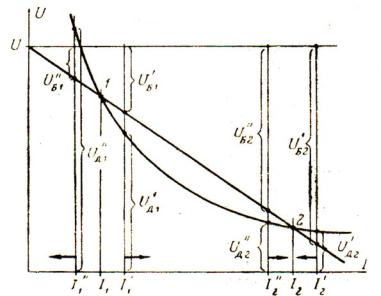
Как видно из рис. 2.39, б, в рассматриваемой цепи возможны два равновесных режима, соответствующих двум токам I1 и I2 в цепи. Однако, как будет
установлено дальше, только один из этих режимов отвечает условию устойчивого равновесия и может быть осуществлен практически.
Исследуем оба найденных режима с точки зрения их устойчивости. Если в первом случае при токе I1 представить отклонение режима в сторону увели-
чения тока (режим при токе I1 на рис. 2.40), то становится очевидным, что сумма напряженийUб1 на балластном резисторе и U Д1 на дуге уже не будет
равна питающему напряжению, а станет меньше, что вызовет увеличение тока, то есть дальнейший отход режима от состояния равновесия. К аналогичному выводу, подтверждающему неустойчивость первого режима, придём, если искусственно выведем цепь из рассматриваемого режима в сторону уменьшения тока до значения I1 . Теперь, как следует из рис. 2.40, сумма напряжений Uб1и
U Д1 преобладает над напряжением U источника, и ток в цепи должен уменьшаться.
Рис. 2.40. Вольт-амперная характеристика дуги
Если рассмотреть отклонение второго режима при токе I2 в сторону его некоторого увеличения (до значения I2 ), то убедимся, что сумма напряжений Uб2 U Д2 становится больше напряжения U источника. Это вызовет умень-
шение тока, то есть возвращение цепи к равновесному режиму. Уменьшение тока от равновесного значения приводит к уменьшению суммы напряжений на приемниках и нарушению равновесия в сторону преобладания питающего на-
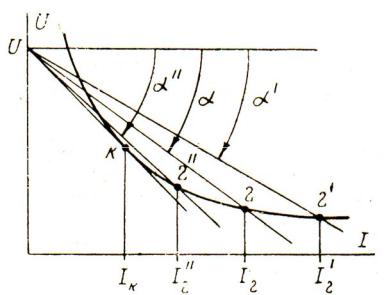
пряжения, что вызывает увеличение тока в цепи, то есть опять-таки возвращение ее режима к равновесию. аким образом, второй режим – при большем из двух соответствующих равновесию токов является устойчивым режимом и всегда устанавливается в цепи в реальных условиях. Первый же режим – при меньшем токе длительно существовать не может.
Регулирование тока дуги проще всего осуществляется посредством изменения сопротивления балластного резистора. Как следует из построений, выполненных на рис. 2.41, уменьшение сопротивления балластного резистора, соответствующее уменьшению угла наклона его характеристики к оси тока, увеличивает ток дуги. Наоборот, увеличение этого сопротивления приводит к уменьшению тока в цепи. При этом горение дуги возможно лишь при ограниченном значении балластного резистора. Если его сопротивление превзойдет величину, соответствующую положению характеристики резистора, при котором она касается характеристики дуги (критический режим, отмеченный на рис. 2.41 точкой k), то характеристики не пересекутся и равновесие в цепи станет невозможным.
Рис. 2.41. Вольт-амперная характеристика при регулировании тока дуги
Любой же из неравновесных режимов в этом случае будет соответствовать преобладанию суммы напряжений на резисторе и дуге над питающим напряжением, то есть уменьшению тока в цепи вплоть до полного его исчезновения.
Таким образом, устойчивый режим горения дуги с заданной характеристикой при токах, меньших критического значения I K , невозможен.
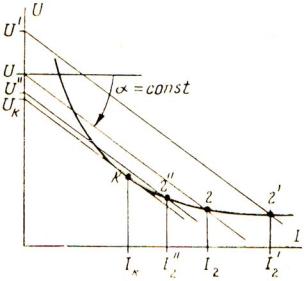
Заметим, кстати, что сам критический режим также является неустойчивым режимом, в чем легко убедиться, исследовав поведение цепи при отклонении режима от критического в сторону уменьшения тока.
Второй способ регулирования тока дуги, проиллюстрированный на рис. 2.42, заключается в изменении напряжения источника U при неизменном сопротивлении балластного резистора. Увеличение напряжения соответствует увеличению тока, а уменьшение напряжения - уменьшению тока. Горение дуги при напряжении, равном или ниже критического напряжения U K , когда харак-
теристика балластного резистора касается характеристики дуги, становится невозможным.
Рис. 2.42. Способ регулирования горения дуги
Пример многозначности режима. В некоторых нелинейных цепях при заданном питающем напряжении возможно установление нескольких устойчивых режимов. Например, в цепи с последовательным соединением линейного балластного резистора Rб и терморезистора R (рис. 2.43, а) при определенных
значениях питающего напряжения U и сопротивления балластного резистора, как вытекает из построений, выполненных на рис. 2.43, б по изложенной выше методике, существуют три равновесных режима, соответствующих трем точкам пересечения характеристик балластного резистора и терморезистора. Исследование устойчивости этих режимов (его учащимся предлагается провести самостоятельно) показывает, что режимы, соответствующие точкам 1 и 3, являются устойчивыми, а режим, отвечающий точке 2, оказывается неустойчивым. Поэтому первый и третий режимы могут длительно существовать на практике, а установить второй режим в реальных условиях не удается.
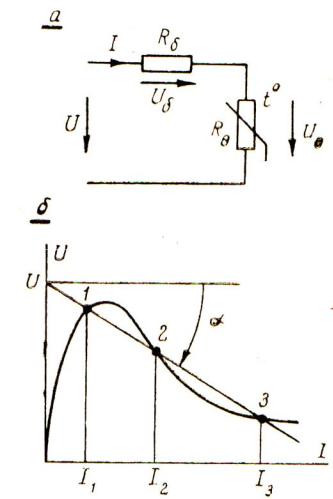
Первый режим – при наименьшем токе I1 можно получить при включе-
нии рассматриваемой цепи под действием не слишком большого питающего напряжения U . Для получения третьего режима необходимо временно повысить питающее напряжение с тем, чтобы «перевалить» режим через горб характеристики терморезистора. После этого напряжение можно снизить до прежнего значения, но ток в цепи уже не вернется к значению I1, а станет равным ве-
личине I3 .
Рис. 2.44. Цепь с терморезистором
Тесты для самопроверки
1. При расчете нелинейных цепей нельзя использовать… а. Метод наложения.
б. Первый закон Кирхгофа.
в. Метод переменных состояний. г. Второй закон Кирхгофа.
2. Нелинейными элементами R, L, C называются…
а. Элементы, параметры которых R, L, C зависят от напряжения или тока. б. Элементы, проводники которых имеют различный диаметр.
в. Элементы, имеющие нелинейную форму.
г. Элементы, параметры которых зависят от атмосферного давления и влажности.
3.Нелинейные свойства емкости обусловлены: а. Нелинейными свойствами диэлектрика.
б. Площадью обкладок конденсатора.
в. Приложенным к конденсатору напряжением. г. Расстоянием между обкладками конденсатора.
4.Нелинейные свойства индуктивности обусловлены: а. Наличием ферромагнитного сердечника.
б. Числом витков обмотки.
в. Размером катушки индуктивности г. Величиной тока в обмотке
5.Укажите ВАХ стабилитрона
|
i |
|
|
|
|
i |
|||
|
|
|
|
||||||
|
|
|
|
|
|
|
|||
а |
u |
|
|
б |
|
|
|
||
|
|
|
|
|
|
|
u |
||
|
|
|
|
|
|
|
|
||
|
i |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
u |
г |
|
u |
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Укажите на характеристиках В(Н) предельный цикл перемагничивания:
B
|
4 |
|
|
3 |
|
а. 4 |
2 |
|
H |
||
|
||
|
1 |
б. 3 в. 2 г. 1
7. Вольт-амперная характеристика U 2I 3 . Определите RCT при I = 2 A
а. 10 Ом. б. 16 Ом. |
в. 24 Ом. |
г. 8 Ом. |
|||||||||||||||||
8. Вебер-амперная |
характеристика 0,1I 3 . Определите динамическую ин- |
||||||||||||||||||
дуктивность Ld при токе I =1 А. |
|
г. 0,15 Гн. |
|||||||||||||||||
а. 0,3 Гн. |
б. 0,1 Гн. |
в. 0,2 Гн. |
|
||||||||||||||||
9. Вебер-амперная |
характеристика 0,1I 3 . Определите статическую индук- |
||||||||||||||||||
тивность LСТ при токе I =1 А. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а. 0,1 Гн. |
б. 1 Гн. в. 10 Гн. г. 0,2 Гн. |
||||||||||||||||||
10. Найдите U, если R1 2 Ом, I=2 A, U2 (I ) 5I 2 . |
|||||||||||||||||||
|
|
|
|
R1 |
|
|
I |
||||||||||||
а. 24 В. |
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б. 4 В. |
|
|
U1 |
|
|
|
|
|
|
|
|
U2 |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||
в. 16 В. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г. 10 В. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. Найдите I, если С=1 мкФ, I2 (U ) 0,04U 2 , а величина постоянного напряже- |
|||||||||||||||||||
нияU 5 В. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
I2 |
|||
а. 1 А. |
|
|
|
|
|
|
I1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б. 2 А. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
С |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
в. 5 А. |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г. 0,04 А. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12. Определите I, если U=10 B, R= 5 Oм, I2 (U ) 0,01U 2 .
|
|
I |
|
|
|
|
||||
а. 3 А. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
б. 6 А. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
в. 2 А. |
|
I1 |
|
|
|
|
|
|
I2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|||||||
г. 8 А. |
|
|
|
|
|
|
|
|
|
|
