Первичные преобразователи. Сокращенный курс

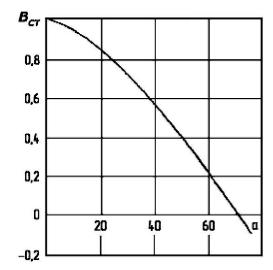
Если в работе использованы продольная и поперечная деформации (измерительный преобразователь установлен под углом к образующей стержня), значения конструктивного коэффициента чувствительности будут определяться степенью использования той или иной деформации. При такой установке последующий измерительный преобразователь будет использовать продольную деформацию, равную εl cosα, и поперечную деформацию (другого знака), равную µεl sinα. Поэтому значения конструктивного коэффициента могут быть вычислены из выражения

BCT = cosα − μ sinα ,

где ВCT – конструктивный коэффициент чувствительности стержня; α – угол установки тензорезистора относительно образующей стержня.

На рис. 2.2.2. дана зависимость коэффициента BСТ от угла а при коэффициенте Пуассона, равном 0,3.

Рис. 2.2.2. Зависимость конструктивного коэффициента чувствительности от угла установки тензорезистора

В соответствии с изложенным, общее выражение функции преобразования стержня может быть представлено в следующем виде:

40

где ВСТ — конструктивный коэффициент чувствительности стержня.

Следовательно, чувствительность стержня определяется конструктивным коэффициентом чувствительности, сечением и модулем упругости материала стержня. Заметим, что деление стержневых упругих элементов на полые и сплошные не изменяет вида функции преобразования.

В случае, если выходной величиной стержневого упругого элемента является перемещение точки приложения силы в направлении ее действия) то функция преобразования

SCT E

где δ – перемещение торца упругого элемента; l – длина упругого элемента.

Как видно из (2.2.5), чувствительность упругого элемента в этом случае зависит от длины.

Другой важной характеристикой любого элемента является его собственная частота колебаний. Для стержневого упругого элемента:

Выражая массу единицы длины упругого элемента через его массу и длину и производя дальнейшие преобразования, получим

m = SCT ρ ,

где ρ – плотность материала.

41

Подставив значение т и константы π в (2.2.6), окончательно получим

Формулы (2.2.3), (2.2.5) и (2.2.7) являются основными при расчете стержневых упругих элементов. Полезно заметить, что анализ выражений (2.2.3 и (2.2.7) позволяет дать определенные рекомендации по совершенствованию данного типа упругих элементов. Так, для повышения чувствительности целесообразно выбирать материал с меньшим модулем упругости. При этом уменьшение собственной частоты колебаний будет происходить медленнее, чем повышение чувствительности, что является выгодным. Увеличение чувствительности без снижения быстродействия достигается уменьшением сечения упругого элемента, а увеличение быстродействия без снижения чувствительности достигается уменьшением длины упругого элемента или выбором материала с меньшей плотностью. Правда, эти возможности лимитированы технологией изготовления и ограниченным перечнем используемых конструкционных материалов.

2.3.Преобразователи давления

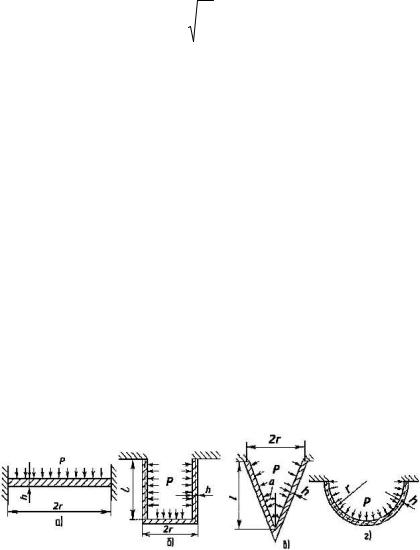
Кпреобразователям давления следует отнести упругие элементы, построенные с использованием различного рода оболочек. Наиболее распространенными и технологичными в изготовлении являются следующие конструкции (рис.2.3.1): мембрана, жестко заделанная по контуру; цилиндрическая оболочка-колпачок толщиной h; полусферическая оболочка толщиной h.

Рис. 2.3.1. Наиболее распрастространенные конструкции упругих элементов, построенных с использованием различного рода оболочек.

42

Мембрана, жестко заделанная по контуру. В таком упругом элементе (рис 2.3.1., а) под действием приложенного давления Р в верхних и нижних волокнах возникают радиальные нормальные напряжения, направленные вдоль радиуса, и окружные нормальные напряжения, направленные по окружности мембраны.

2.4. Датчик линейных перемещений и угла поворота Основное дифференциальное уравнение упругой линии

С установлением связи между деформациями и внутренними силами при изгибе мы столкнулись при выводе формулы для нормальных напряжений

σ = M y z . IY

Зависимость кривизны в данной точке оси от изгибающего момента Му и жесткости балки при изгибе Е1у, получим:

Для удобства дальнейших операций необходимо принять та-

1

кое правило знаков для кривизны ρ x ,при котором ее знак будет

всегда совпадать с принятым нами знаком изгибающего момента в том же сечении. Это приводит нас к правилу, согласно которому кривизна положительна, если упругая линия в данной точке обращена выпуклостью вниз (тот же знак мы имеем и для изгибающего момента). В соответствии с этим условием в дальнейшем направим ось z вверх.

Дифференциальное уравнение упругой линии имеет вид:

43

Для изучаемых нами малых деформаций можно пренебречь в знаменателе величиной квадрата первой производной* по сравнению с единицей, и тогда получим так называемое приближенное дифференциальное уравнение упругой линии

правила знаков:

1.Прогиб считается положительным, если он направлен

вверх.

2.Угол поворота считается положительным, если касательная к упругой линии в данной ее точке, параллельно перенесенная в начало координат, проходит в нечетных квадрантах координатной системы.

Исследование деформаций балок с одним грузовым участком

Перейдем к практическому использованию приближенного дифференциального уравнения упругой линии и рассмотрим эту задачу в общем виде.

Интегрируя уравнение (2.4.5), получим

44

Интегрируя выражение угла поворота (2.4.8), получаем уравнение упругой линии z = f(x)

В выражениях (2.4.5) и (2.4.6) С и D являются произвольными постоянными. Эти интегрирования возможны, если изгибающий момент Му является непрерывной функцией от х, то есть Му = f(x), что, как мы знаем, имеет место лишь в пределах одного грузового участка. Поэтому число дифференциальных уравнений будет равно числу грузовых участков балки. Для каждого такого участка мы получим при интегрировании две произвольные постоянные, и, таким образом, если балка имеет n грузовых участков, то число произвольных постоянных будет 2n.

Из математики известно, что произвольные постоянные не влияют на очертание кривой, выражающей найденную функцию, но определяют положение этой кривой в принятой системе координат. Это обстоятельство дает нам способ для определения постоянных интегрирования, при которых упругая линия займет то положение, которое диктуется характером закрепления балки на ее опорах и при котором сопряжение отдельных кривых на границах грузовых участков будет удовлетворять условиям плавности и непрерывности. Этих условий бывает достаточно, чтобы составить 2п уравнений для определения 2п постоянных интегрирования. Все высказанные соображения будут разъяснены ниже при рассмотрении частных случаев.

Сначала рассмотрим балку, защемленную одним концом, с одним грузовым участком и нагруженную равномерно распределенной нагрузкой, интенсивностью q (рис. 2.4.1).

45

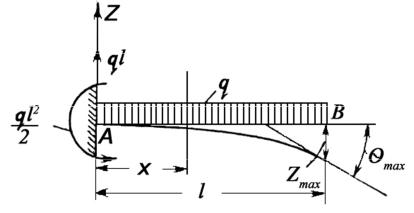
Рис. 2.4.1

Начало координат поместим в защемленном конце, ось х направим вправо. Значения опорных реакций в защемлении указаны на рисунке. Напишем выражение для изгибающего момента в сечении х.

Дифференциальное уравнение упругой линии в этом случае напишется в виде:

Интегрируя это уравнение последовательно два раза, получим

Для определения произвольных постоянных С и D воспользуемся условиями закрепления балки. В защемленном конце балки, как известно, прогиб и угол поворота равны нулю. Эти условия математически можно записать в таком виде:

46

После использования указанных граничных условий в зависимостях (2.4.8) и (2.4.9) получим, что произвольные постоянные равны нулю, то есть С = 0 и D = 0. После подстановки этих значений в те же уравнения (2.4.8) и (2.4.9) получим окончательные выражения углов поворота и прогиба для любого сечения

Последнее уравнение показывает, что для рассматриваемого случая упругая линия изменяется по закону параболы четвертой степени.

Вопросы для самоконтроля освоения знаний по главе 2

1.Перечислите механические физические величины и виды упругих элементов, используемых при конструировании преобразователей силы.

2.Перечислите виды упругих элементов, преобразующих силу в давление.

3.Перечислите виды упругих элементов, преобразующих силу в деформацию.

4.Приведите функции преобразования для упругого стержня постоянного сечения для продольной и поперечной (сдвиговой) деформаций.

5.Как расчитать чувствительность упругого стержня к продольной и поперечной деформациям?

6.Перечислите наиболее распространенные упругие элементы, используемые для измерения давления, построенные на базе различного рода оболочек.

7.Приведите основное дифференциальное уравнение упругой

линии.

8.Каким образом можно измерить линейное перемещение и угол поворота при использовании чувствительного элемента в виде

47

упругой балки с одним грузовым участком? Как выглядят функции преобразования и чувствительность к измеряемым величинам?

9. По какому признаку упругий стержень и упругие балки не соответствуют определению первичный преобразователь? Каким образом необходимо создать измерительную цепь, чтобы обеспечить соответствие?

ГЛАВА 3. ЕМКОСТНЫЕ (КОНДЕНСАТОРНЫЕ) ДАТЧИКИ – ПРЕОБРАЗОВАТЕЛИ

Емкостные датчики преобразуют механическое перемещение (линейное или угловое) в изменение электрической емкости конденсатора. Емкостный датчик представляет собой конденсатор, состоящий из двух или более пластин, разделенных слоем воздуха или другим диэлектриком [2] и [4].

Емкость плоского конденсатора определяется известной фор-

δ — величина зазора между пластинами, см.

Из приведенной формулы видно, что изменения емкости можно достигнуть путем изменения значения одной из величин δ, s и ε. Соответственно могут быть изготовлены различные типы емкостных датчиков, в которых, в зависимости от измеряемого перемещения, изменяется один из этих параметров, остальные остаются постоянными.

На рис. 3.1. приведены принципиальные схемы емкостных датчиков перемещения и их характеристики в зависимости от изменяемого параметра.

48

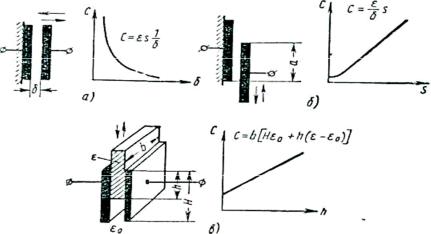
Рис.3.1. Принципиальные схемы емкостных датчиков перемещения с их характеристиками.

Различают три типа емкостных датчиков перемещения: датчики с переменным зазором, датчики с переменной площадью пластин конденсатора и датчики с переменной диэлектрической проницаемостью.

На рис. 3.1, а показана схема датчика с переменным зазором δ. Характеристика этого датчика С = f (δ ) при постоянных значе-

ниях ε и s изменяется по гиперболическому закону; на рис. 3.1, б представлена схема датчика с переменной площадью пластин конденсатора. Его характеристика С = f (s) при постоянных

значениях δ и ε изменяется почти линейно; наконец, на рис. 3.1, в изображена схема датчика с переменной диэлектрической проницаемостью.

Его характеристика С = f (ε ) при постоянных значени-

ях δ и s также изменяется линейно.

Потребляемая конденсатором мощность

Р = U2 ωC ,

где U — напряжение переменного тока, В; ω — частота переменного тока, рад/с; С — емкость конденсатора, Ф.

49