
kursov_vectors
.pdf
Аналогично, условным распределением компоненты Y при условии, что называется совокупность условных вероятностей
y |
|
y |
2 |
x |
|
y |
n x |
|
|
P |
1 x |
,P |
,...,P |
, |
|||||
|
|
i |
|
|
i |
|
|
i |
|
которые вычисляются по формулам
Y y j |
|
|
y j |
|
|
P X xi , Y y j pij |
|
|||||||||||||||||
P |
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
P X xi |
|
|
pi |
|
||||||||||||||||
|
X xi |
|
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
Y yj |
x |
|
|
равны: |
||||||||||||
Согласно формулам (1.2), условные вероятности P |
|
|
X |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||
Y y |
|
|
|
|
|
|
|
0,2 |
1 |
|
|
|
|
|||||||||||
P |
1 X x |
P Y 1 X 0 |
|
|
|
|
|
|
|
, |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
1 |
|
P Y |
0 X 0 |
0,6 |
3 |
|
|
|
|
||||||||||||
Y y |
2 X x |
|
0,1 |
|
1 |
|
|
|
|
|
||||||||||||||
P |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
||||||||||
|
0,6 |
|
|
|
|
|
||||||||||||||||||
|
|
|
1 |
P Y |
1 X 0 |
|
6 |
|
|
|
|
|
||||||||||||
Y y |
3 X x |
|
0,3 |
|
|
1 |
|
|
|
|
|
|
||||||||||||
P |
|
|
|
|
|
|
|
|
. |
|
|
|||||||||||||
|
0,6 |
|
|
|
|
|||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
X xi , i const
(1.2)
Y y |
j |
|
|
определяются соотношениями: |
Аналогично, условные вероятности P |
X |
|
||
|
|
x2 |
|
Y y |
|
|
|
|
|
0,1 |
|
1 |
|
|||||||||||
P |
1 |
P Y 1 |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||||
0,4 |
4 |
|||||||||||||||||||
|
|
|
X x2 |
|
|
X 1 |
|
|
||||||||||||
Y y |
2 |
|
|
P Y 0 |
|
|
0,2 |
|
|
1 |
|
|
||||||||
P |
|
X x2 |
|
|
|
|
|
|
|
|
|
|
|
, |
||||||
|
|
0,4 |
|
2 |
||||||||||||||||
|
|
|
|
|
|
X 1 |
|
|
|
|
||||||||||
Y y |
3 |
|
P Y 1 |
|
|
0,1 |
|
|
|
1 |
|
|
|
|||||||
P |
|
|
|
|
|
|
|
|
|
. |
||||||||||
|
|
0,4 |
|
|
||||||||||||||||
|
|
|
X x2 |
|
|
X 1 |
|
|
|
4 |
|
|
|
|||||||
По вычисленным условным вероятностям можно составить условные законы распределения случайной величины Y (табл. 3).
Таблица 4. Условные законы распределения случайной величины X .
Y |
|
|
–1 |
|
0 |
|
1 |
|
|
|||
Y y j |
|
1 |
|
|
1 |
|
1 |
|
|
|||
P |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
6 |
|
2 |
||||||
|
|
X 0 |
|
|
|
|
|
|||||
Y y |
|
|
1 |
|
|
1 |
|
1 |
|
|
||
P |
j |
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
|
2 |
|
4 |
||||||
|
|
X 1 |
|
|
|
|
|
|||||
Вычислим условные вероятности |
X x |
i |
|
для |
|
i 1, 2 , |
j 1, 2, 3 по формулам |
|||||||||||||
P |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
Y y j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X x |
|
|
|
|
|
|
|
|
0,2 |
|
|
2 |
|
|
|
|||||
P |
1 |
|
P X 0 |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|||
|
|
|
0,3 |
3 |
|
|||||||||||||||
|
|
|
Y y1 |
|
Y 1 |
|
|
|
|
|||||||||||
X x |
2 |
|
|
P X 1 |
|
|
|
0,1 |
|
|
1 |
|
|
|
||||||
P |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||
|
|
|
|
0,3 |
|
|
|
|||||||||||||
|
|
|
Y y1 |
|
Y 1 |
|
3 |
|
|
|
||||||||||
X x |
|
|
P X 0 |
|
|
|
0,1 |
|
|
|
1 |
|
|
|
|
|||||
P |
|
1 |
|
Y 0 |
|
|
|
|
|
|
, |
|
||||||||
|
0,3 |
|
|
3 |
|
|||||||||||||||
|
|
|
Y y2 |
|
|
|
|
|
|
|
|
|
|
|||||||
21

X x |
|
|
|
|
0,2 |
2 |
|
||
P |
2 |
|
P X 1 |
Y 0 |
|
|
|
|
. |
|
|
||||||||
|
|
Y y2 |
|
0,3 |
3 |
|
|||
X |
x |
|
|
|
P X 0 |
|
0,3 |
|
|
3 |
|
|
|
P |
1 |
|
|
|
|
|
|
|
, |
||||
|
0,4 |
4 |
|||||||||||
|
Y |
y3 |
|
Y |
1 |
|
|
|
|
||||
X x |
|
|
|
P X 1 |
|
0,1 |
|
|
1 |
||||
P |
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
0,4 |
|
4 |
|||||||||
|
|
|
Y y3 |
|
Y 1 |
|
|
|
|||||
Условные законы распределения случайной величины X даны в таблице 4.
Таблица 5. Условные законы распределения случайной величины Y .
X |
|
|
|
0 |
|
1 |
|
|
|
X xi |
|
|
|
2 |
|
1 |
|
|
|
P |
|
|
|
|
|
|
|
|
1 |
|
3 |
|
3 |
||||||
|
Y 1 |
|
|
|
|
||||
X xi |
|
|
1 |
|
2 |
|
|
||
P |
|
|
|
|
|
|
|
|
1 |
|
3 |
|
3 |
||||||
|
|
Y 0 |
|
|
|
|
|||
X xi |
|
|
3 |
|
1 |
|
|
||
P |
|
|
|
|
|
|
|
|
1 |
|
4 |
|
4 |
||||||
|
|
Y 1 |
|
|
|
|
|||
4. Условные законы распределения не совпадают с безусловными законами, поэтому случайные величины X и Y зависимы. Убедиться в том, что случайные величины X и Y связаны функциональной зависимостью, можно также сравнивая закон совместного распределения случайного вектора (табл.1) с маргинальными законами (табл. 2 и табл. 3).
P X 0, Y 1 p11 0,2 ,
P X 0 p1 0,6 , P Y 1 q1 0,3 .
Следовательно, P X 0, Y 1 p11 P X 0 P Y 1 p1 q1 0,6 0,3 0,18 .
5. По маргинальным законам распределения случайных величин X и Y (табл. 2 и 3) найдем их математические ожидания, дисперсии и средние квадратичные отклонения, а также числовые характеристики совместного распределения, т.е. корреляционный момент и коэффициент корреляции.
а) Математические ожидания:
m
M X xi pi 0 0,6 1 0,4 0,4 .
i 1
n
M Y yj qj 1 0,3 0 0,3 1 0,4 0,1.
j 1
Математическим ожиданием случайного вектора является вектор
M X ; M Y 0,4; 0,1 .
б) Дисперсии:
m
D X xi2 pi M X 2 0 0,6 1 0,4 0,16 0,24 .
i 1
n
D Y y2j qj M Y 2 1 0,3 0 0,3 1 0,4 0,01 0,69 .
j 1
в) Средние квадратичные отклонения:
22

X 
 D X
D X 
 0,24 , Y
0,24 , Y 
 D Y
D Y 
 0,69 .
0,69 .
г) Корреляционный момент (ковариация) и корреляционная матрица (матрица ковариаций).
Чтобы найти корреляционный момент (ковариацию) случайного вектора, необходимо вычислить математическое ожидание случайной величины XY :
m n
M XY xi yj pij 0 1 0,2 0 0 0,1 0 1 0,3 1 1 0,1 1 0 0,2 1 1 0,1 0 .
i 1 j 1
Тогда ковариация KXY , вычисленная по формуле KXY M XY M X M Y , равна:
KXY KYX 0 0,4 0,1 0,04 .
Корреляционная матрица (матрица ковариаций) имеет вид:
D X |
K |
|
0,24 |
0,04 |
|
|||
|
K |
|
|
XY |
|
0,04 |
0,69 |
. |
|
YX |
D Y |
|
|
||||
|
|
|
|
|
|
|
|
|
Определитель матрицы ковариаций – обобщенная дисперсия случайного вектора:
|
|
|
|
0,24 |
0,04 |
0,24 0,69 0,042 0,164 . |
|
|
|||||
|
|
0,04 |
0,69 |
|||
|
|
|
|
|
д) Коэффициент корреляции.
Коэффициент корреляции между случайными величинами X и Y определяется формулой:
rXY |
|
KXY |
|
|
0,04 |
|
|
|
2 |
|
. |
|||||
X |
Y |
|
|
|
|
|
|
|
|
|
||||||
0,24 0,69 |
26 |
|||||||||||||||
|
|
|
|
3 |
|
|
||||||||||
6. Функции и линии регрессии.
Условным математическим ожиданием дискретной случайной величины X при Y y
называется сумма произведений возможных значений случайной величины X на соответствующие условные вероятности, т.е.
М X
Условное математическое
m
Y y
i 1
ожидание
xi |
X xi |
|
|
P |
Y |
. |
|
|
|
y |
|
случайной |
величины |
||
(1.3)
X , при Y y , т.е.
|
|
|
|
y , является функцией переменной y и называется функцией регрессии или |
||||||
М X |
m |
X |
||||||||
|
Y y |
|
|
|
|
|
|
|
|
|
регрессией случайной величины X на Y . |
|
|
|
|
|
|||||
Условным математическим ожиданием дискретной случайной величины Y |
при X x |
|||||||||
называется сумма произведений возможных значений случайной величины Y |
на |
|||||||||
соответствующие условные вероятности, т.е. |
|
|
|
|
|
|||||
|
|
|
|
|
n |
Y y j |
|
(1.4) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
М Y X x y j P |
X x . |
|
|
|||
|
|
|
|
|
j 1 |
|
|
|
|
|
Условное |
математическое |
ожидание |
случайной |
величины |
Y , при |
X x , |
т.е. |
|||
М Y X x mY x , функцией переменной x |
и называется функцией регрессии или регрессией |
|||||||||
случайной величины Y на X . |
|
|
|
|
|
|
||||
Найдем регрессию mY x |
случайной величины Y |
на X , используя условные законы |
||||||||
распределения случайной величины Y (табл. 4) и формулу (1.3):
23
при X 0 , m |
x |
|
m |
0 1 |
1 |
|
0 |
1 |
|
1 |
1 |
|
|
1 |
, |
|
|||
|
|
|
|
|
|
|
|
||||||||||||
Y |
1 |
Y |
|
3 |
|
|
6 |
|
|
2 |
|
6 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
при X 1, m |
x |
2 |
m |
1 1 |
1 |
|
0 |
1 |
1 |
1 |
0 . |
|
|||||||
|
|
|
|
|
|||||||||||||||
Y |
|
Y |
|
4 |
|
|
2 |
|
4 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
xi ; mY xi и |
||||||||
Линии регрессии |
принято |
строить |
|
ломаными, соединяющими точки |
|||||||||||||||
y j ; mX y j , хотя по сути – это набор таких точек. Линией регрессии Y на X |
будет отрезок |
||||||||||||||||||
прямой, проходящей через точки |
0; 1 и |
|
1; 0 |
|
на плоскости с введенной системой координат |
||||||||||||||
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|||
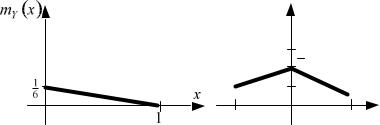
x, mY x . Эта линия регрессии показана на рисунке 2 a.
Рис. 2 a. Линия регрессии Y на X . |
mX y |
|
|
1 |
2 |
|
|
3 |
|
1 |
y |
|
3 |
||
|
||
1 |
1 |
|
Рис. 2 b. Линия регрессии X на Y . |
||
При определении регрессии |
mX y |
случайной величины X на Y , используем условные |
||||||||||||||||||||||||||||||||||||
законы распределения случайной величины X (табл. 5) и формулу (1.4): |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
при Y 1 |
. m |
X |
y |
|
|
m |
X |
1 0 |
2 |
|
1 |
1 |
|
|
1 |
, |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
1 |
|
|
|
3 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
при Y 0 , |
mX y2 |
mX |
0 0 |
1 |
1 |
2 |
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
при Y 1, |
mX y3 |
mX |
|
1 0 |
3 |
1 |
1 |
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
4 |
|
4 |
|
|
1; |
|
, |
0; |
|
и |
1; |
|
|
||||||||||||
Линией регрессии |
X на Y |
будет ломаная, проходящая через точки |
1 |
2 |
1 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
4 |
|
на плоскости с введенной системой координат y, mX y . Эта линия регрессии показана на рисунке 2. b.
24
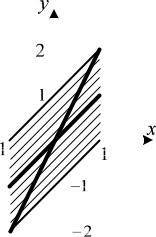
Задача №1
Постановка задачи
Задана плотность совместного распределения случайных величин X и Y
0, |
x, y D |
|
f x, y C, |
x, y D |
, |
|
|
|
где область D : |
|
|
D x, y : 1 x 1, x 1 y x 1 .
Найти:
параметр C ;
плотности распределения компонент случайного вектора X и Y ;
функции распределения компонент случайного вектора X и Y ;
условные плотности f x Y y и f y
Y y и f y X x ;
X x ;
выяснить, являются ли независимыми компоненты случайного вектора X и Y ;
числовые характеристики случайного вектора: математические ожидания и дисперсии случайных величин X и Y , корреляционный момент и коэффициент корреляции, корреляционную матрицу и обобщенную дисперсию;
функции регрессии (условные математические ожидания) Y на X и X на Y , построить линии регрессии.
Решение |
D показана на рисунке 3. Из свойств плотности распределения следует, что |
|||||||||||||||||
1. Область |
||||||||||||||||||
C |
1 |
|
|
|
1 |
, где S D - площадь области D . поскольку S D 2 2 4 . |
||||||||||||
S D |
4 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.
Тогда для плотности совместного распределения справедливы соотношения:
25
|
0, |
x, y D |
|
f x, y |
1 |
, |
x, y D . |
|
|||
4 |
|
|
|
2.Плотности распределения компонент (маргинальные или частные плотности) случайного вектора найдем, используя формулы
|
|
|
f X x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
f x, y dy , |
|
|
|
|
|
(2.1) |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
fY y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
f x, y dx . |
|
|
|
|
|
(2.2) |
|
|
|
||||||||||||||||||||||||||||
а) При x 1;1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f X x 0 , т.к. при этом условии |
|
|
f x, y 0 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
При x 1; 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
f X x f x, y dy |
1 |
dy |
1 |
|
y |
|
|
1 |
x 1 x 1 |
1 |
|
. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
4 |
4 |
x 1 |
4 |
2 |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Следовательно, случайная величина X распределена равномерно на отрезке 1; 1 , т.е. |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
, |
|
|
|
x 1;1 |
. |
|
|
(2.3) |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
f X x |
2 |
|
|
|
x 1;1 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
б) При y 2; 2 |
fY y 0 , т.к. при этом условии f x, y 0. |
|||||||||||||||||||||||||||||||||||||||||||
При y 2; 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
fY y f x, y dx |
|
|
|
1 |
dx |
1 |
|
x |
|
|
|
1 |
y 1 1 |
|
1 |
y |
1 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
. |
||||||||||||||||||||||||||||||||||||||
4 |
4 |
|
|
4 |
4 |
2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
При y 0; 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
fY y f x, y dx |
1 |
dx |
1 |
x |
|
1 |
1 y 1 |
1 |
|
|
1 |
y . |
||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
4 |
4 |
|
|
4 |
2 |
4 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
y 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следовательно, плотность распределения компоненты Y имеет вид: |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
y |
|
1 |
|
y |
1 |
, 2 y 0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
f |
|
|
|
2 |
(2.4) |
|
|
|
|||||||||||||||||||||||||||||||||||
|
Y |
4 |
1 |
|
|
1 |
|
|
|
|
|
|
|
. |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
y |
|
|
, 0 y 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
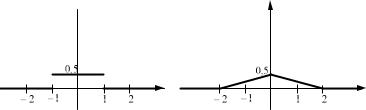
Графики функций f X x и fY y показаны на рисунке 4.
fX x 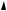
x
fY y |
y |
Рис. 4.
3.Функции распределения случайных величин X и Y определяются по известным плотностям формулами
26
|
|
|
|
|
|
|
FX x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
f X t dt , |
|
|
|
|
|
|
FY y f X t dt . |
(2.5) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
По этим формулам, учитывая вычисленные плотности |
f X x |
и fY y |
(см. (2.3) и (2.4)), |
||||||||||||||||||||||||||||||||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
x 1 |
|
|
|
|
0, |
|
x 2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
dt, 1 x 1= |
1 |
x 1 , 1 x 1 , |
|
|
|||||||||||||||||||||||||
|
|
|
FX |
x |
|
1 |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
2 |
|
|
||||||||||||||||||||||||||||||||||||
|
2 |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1, |
|
x 2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1, |
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
0, |
|
|
|
|
|
y 2 |
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
y 2 |
|
||||||||||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
t |
1 |
dt, 2 |
y 0 |
|
|
|
|
|
|
81 t2 |
t |
|
|
|
, 2 y 0 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||
FY y |
0 |
|
2 |
y |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
y |
= |
||||||||||
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
dt |
|
|
dt, 0 y 2 |
|
|
|
|
|
|
|
t |
|
|
|||||||||||||||||||||||
|
4 |
t |
2 |
4 |
t |
2 |
|
1 |
81 t2 |
1 |
, 0 y 2 |
||||||||||||||||||||||||||||
2 |
2 |
||||||||||||||||||||||||||||||||||||||
2 |
|
0 |
|
|
|
|
y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||||||||||||
|
|
|
|
|
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, |
|
|
|
y 2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
y 2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
y2 |
|
1 |
|
y |
1 |
|
, 2 |
y 0 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
8 |
1 |
2 |
|
1 |
|
1 |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 y |
|
|
|
|
y |
|
|
|
, 0 y |
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, |
|
|
|
y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Графики функций распределения FX x |
и FY y показаны на рис. 5. |
|
|||||||||||||||||||||||||||||||||||||
|
F x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FY y |
|
|
|
|
|
|||||
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Рис. 5. |
|
|
|
|
|
|
|
|
|
|
||
4. Условные плотности распределения |
f x Y y и |
f y |
X x определяются из |
||||||||||||||||
соотношений: |
|
|
|
|
|
|
fY y 0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
||||||
|
|
|
f x Y y f x, y |
, |
fY y 0 |
, |
(2.6) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
fY y |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
f X x 0 |
|
|
|
|
|
||||||
|
|
|
f y |
|
0, |
|
|
|
|
|
|
||||||||
|
|
|
X x f x, y |
, |
f X x 0 |
. |
(2.7) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
f X x |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
27

|
0, |
|
|
y 2 |
|
0, |
|
|
y 2 |
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
4 |
|
, 2 y 0 |
|
1 |
, 2 y 0 |
|
||||||||
|
1 |
y |
1 |
|
|
|
|||||||||
|
|
||||||||||||||
f x Y y 4 |
1 |
2 |
|
|
|
|
y 2 |
|
|
|
(2.8) |
|
|||
|
|
|
|
|
|
|
1 |
|
, 0 y 2 |
|
|||||
4 |
|
|
, 0 y 2 |
|
|
||||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
y 2 |
|
|
|
||||||
|
1 |
y |
|
1 |
|
|
|
||||||||
|
|
|
2 |
|
|
|
|
0, |
|
|
y 2 |
|
|
||
4 |
y 2 |
|
|
|
|
||||||||||
|
0, |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f y |
|
|
1 |
, |
x 1; 1 |
. |
(2.9) |
|
|||||
|
|
|
|
|
|||||||||||
|
|
X x 2 |
x 1; 1 |
|
|||||||||||
|
|
|
|
|
|
0, |
|
f x Y y и f y |
X x |
||||||
5. В рассмотренном примере условные плотности распределения |
|||||||||||||||
(2.6) и (2.7) не совпадают с безусловными плотностями f X x |
и fY y (2.8.) и (2.9). Это |
||||||||||||||
имеет место тогда и только тогда, когда случайные величины X и Y зависимы. |
|
||||||||||||||
6. Числовые характеристики случайного вектора. |
|
|
|
|
|
|
|||||||||
а) математическое ожидание; |
|
|
|
|
|
|
f X x и |
fY x компонент |
|
||||||
По вычисленным плотностям распределения |
вектора |
||||||||||||||
вычислим математическое ожидание, определив математические ожидания его компонент по формулам:
|
|
|
|
|
|
|
M X |
|
|
|
|
|
|
|
|
|
|
|
|
|
M Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
x f X x dx , |
|
|
|
|
|
|
|
|
y fY y dy . |
|
|
|
(2.10) |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
M X |
1 |
1 |
|
|
|
|
|
|
1 |
|
x2 |
|
1 0 , |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
M Y y |
y |
dy y |
|
y |
dy |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
2 |
4 |
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
0 |
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
y3 |
y |
2 |
|
0 |
|
|
|
|
|
y3 |
y2 |
|
2 |
|
8 |
|
8 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
4 |
y |
|
|
2 |
y dy |
4 |
y |
|
|
2 y dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
12 |
1 |
12 |
1 0 . |
|||||||||||||
|
2 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
12 4 |
|
2 |
|
|
|
|
|
|
|
|
4 |
|
0 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Следовательно, математическим ожиданием случайного вектора является нулевой числовой
вектор 0; 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) Корреляционный момент (ковариация) KXY вычисляется по формуле |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
K XY M XY M X M Y , |
|
|
|
|
|
(2.11) |
|
|
|
|
|
|
|
|
||||||||||
где M XY – математическое ожидание случайной величины XY . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Поскольку M X M Y 0 , то вычислив |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
1 |
1 |
|
x 1 |
1 |
1 |
|
y |
2 |
|
x 1 |
|
|||||||||||||
|
|
|
|
|||||||||||||||||||||||
M XY |
xyf x, y dxdy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
xydxdy |
|
|
xdx ydy |
|
|
|
xdx |
|
|
|
|
|
|
|
|||||||||||
4 |
4 |
4 |
2 |
|
|
x 1 |
||||||||||||||||||||
|
|
D |
1 |
x 1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||
|
1 |
1 |
|
|
|
1 |
|
1 |
1 x |
3 |
|
|
1 |
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x x2 2x 1 x2 2x 1 dx |
|
x2dx |
|
|
|
|
|
, |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
4 |
1 |
|
|
|
2 |
|
1 |
2 3 |
|
1 3 |
|
|
|
|
|
|||||||||||
найдем по формуле (2.11) ковариацию случайных величин Х и Y .
28

K XY M XY M X M Y 1 .
3
в) Корреляционной матрицей (матрицей ковариаций) случайных величин Х и Y
называется симметричная квадратная матрица второго порядка, на главной диагонали которой
расположены дисперсии случайных величин |
Х |
|
и Y , а на побочной диагонали – |
||
корреляционные моменты, т.е. |
|
|
|
|
|
D X |
K |
XY |
|
||
|
K |
|
|
. |
|
|
YX |
D Y |
|||
|
|
|
|
|
|
Определитель матрицы величин Х и Y , т.е.
D X
KYX
ковариаций называется обобщенной дисперсией случайных
K XY |
2 2 |
2 |
– обобщенная дисперсия. |
D Y |
X Y |
K XY |
|
|
|
|
Поскольку ковариация случайных величин |
Х |
|
|
|
и |
Y K XY |
|
1 |
|
|
, то, |
вычислив дисперсии |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
случайных величин Х и Y , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
3 |
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
D X x2 fX x dx M X |
|
|
x2 dx 0 |
1 |
|
|
x |
|
1 |
|
13 , |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
2 |
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
D Y y2 fY y dy M Y 2 y2 |
1 |
|
|
|
y |
1 |
dy y2 |
1 |
y |
1 |
dy 0 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4 |
|
2 |
4 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y3 |
|
|
y2 dy |
|
y3 |
y2 |
dy 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
2 |
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
y |
4 |
|
|
|
|
|
y3 |
|
0 |
|
|
|
|
|
y4 |
|
|
|
|
|
|
|
y3 |
|
2 |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
8 2 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
, |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
6 3 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
16 |
|
6 |
|
2 |
|
|
|
|
|
|
|
|
|
|
6 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
составим матрицу |
ковариаций |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
которой |
|
является обобщенная |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3 |
3 , определителем |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
дисперсия, т.е. |
|
|
|
|
1 |
|
2 |
|
1 |
|
|
1 |
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
3 |
3 |
|
3 |
|
|
3 |
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
г) Коэффициент корреляции вычисляется по формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rXY |
|
|
KXY |
|
, |
|
|
|
|
|
|
|
|
|
|
(2.12) |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
где X и y - средние квадратичные отклонения случайных величин Х и Y . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||||||||||||||||||||||
Поскольку X |
|
|
|
|
|
|
|
|
|
|
|
, Y |
|
|
|
|
|
|
|
, то rXY |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
D X |
|
|
|
D Y |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
7.Функции регрессии (условные математические ожидания) строятся по найденным условным плотностям распределения (2.8) и (2.9) по формулам:
29

mX y M X Y y |
|
|
|
x f x Y y dx – функция регрессии X на Y ; |
|||
|
|
|
|
|
|
|
|
mY x M Y |
X x |
y f y |
X x dy – функция регрессии Y на X . |
Поэтому регрессия X на Y определяется соотношениями: при y 2 , mX y 0 ;
при 2 y 0 ,
mX y x f x Y y dx y 1 x |
|
1 |
dx |
1 |
|
|
|
x2 |
|
y 1 |
y 1 2 1 |
|
|
y2 2y |
|
|
y |
. |
||||||||||||||||||
|
|
|
y 2 2 |
2 y 2 |
2 y 2 |
|
|
|||||||||||||||||||||||||||||
|
|
|
y 2 |
|
|
1 |
|
|
2 |
|
||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
при 0 y 2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
1 x |
2 |
|
|
|
1 |
|
2 |
|
|
|
y |
2 |
2y |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
mX y x f x Y y dx x |
|
|
dx |
|
|
|
|
|
|
|
|
1 y 1 |
|
|
|
|
y |
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2 y 2 |
|
|
|
2 2 y |
2 2 y |
|
||||||||||||||||||||||||||
|
y 1 2 y |
|
y 1 |
|
|
|
2 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
при y 2 , mX y 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
y 2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
mX y |
|
, 2 y 2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
2 |
|
0. y 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Линия регрессии X на Y : x mX y |
или x |
y |
, |
при 2 y 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Определим регрессию Y на X : при x 1 , mY x 0 ;
при 1 x 1 ,
mY x y f y
при x 1 , mY x 0 . Следовательно,
X x dy |
x 1 |
1 |
|
1 |
|
y2 |
|
x 1 |
x 1 2 x 1 2 |
|
|
|
ydy |
|
|
|
x ; |
||||||
2 |
2 |
2 |
4 |
||||||||
|
x 1 |
|
|
x 1 |
|
||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
0, |
|
x 1, |
m |
x |
x, |
1 x 1, |
||
Y |
|
|
|
|
|
|
|
|
0. |
x 1. |
|
|
|
|
|||
Линия регрессии Y на X : y mY x или y x , |
при 1 x 1 . Линии регрессии |
показаны на рис. жирными линиями. Поскольку линии регрессии являются прямыми, то регрессия линейная.
Из вида линий регрессии понятно, что случайные величины Х и Y не являются независимыми, поскольку линиями регрессии независимых случайных величин являются
30
