
отчет по лаб 7
.docxМинистерство образования и науки РФ
Национальный минерально-сырьевой университет «Горный»
Отчет
По лабораторной работе №7
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДЫХ ТЕЛ С ПОМОЩЬЮ МАЯТНИКА МАКСВЕЛЛА
Выполнил: студент группы ГНГ-12 Сляднева Д.А.
Проверил: Ремзова Е.С.
1.Цель работы - изучение маятника Максвелла и определение с его помощью момента инерции твердых тел.
2. Краткое теоретическое содержание
Маятник Максвелла представляет собой однородный диск , через центр которого проходит металлический стержень . К концам этого стержня прикреплены две нити. Они тщательно, виток к витку, наматываются на стержень в направлении от его конца к диску. При этом диск на стержне поднимается вверх. Если не удерживать диск в верхнем положении, то возникает поступательное движение маятника вниз и его вращательное движение вокруг оси симметрии. Вращение, продолжаясь по инерции в низшей точке движения (когда нити уже размотаны), приводит вновь к наматыванию нити на стержень. Диск снова поднимается вверх и движение повторяется, т.е. возникают колебания.
Момент инерции тела является мерой инертности тела при вращательном движении. Момент инерции тела зависит от размеров и формы тел и от распределения массы тела относительно оси вращения.
При выводе расчётных формул использованы соотношения для моментов инерции тел, и закон сохранения полной механической энергии.
Теоретическое значение момента инерции маятника Максвелла Jт можно определить в виде суммы моментов инерции, для его трёх элементов: оси маятника, диска и кольца, надетого на диск
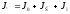
В формуле:
момент
инерции оси маятника
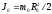 ;
;
момент
инерции диска
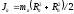
момент
инерции кольца, надетого на диск
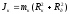 ;
;
здесь Rо, m0, Rд, mд, Rк, mк - соответственно радиусы и массы оси, диска и кольца Кинетическая энергия маятника массой m, поднятого и зафиксированного на высоте h, равна нулю. Полная механическая энергия определяется только потенциальной энергией Eп = mgh.
В нижнем положении
маятника Eп = 0, и полная механическая
энергия равна сумме кинетических энергий
поступательного
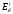 и вращательного
и вращательного
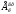 движений
движений
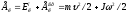 , где
, где
Из закона сохранения следует, что полная энергия маятника в верхнем и нижнем положениях должна быть одинакова, т.е.
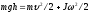
Отсюда момент инерции маятника
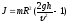 .
.
3.Основные расчетные формулы.
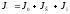 ,где
,где
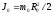 ,
,
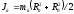 ,
,
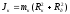 ;
;
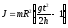
4.Формулы погрешностей.
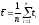 ;
;
 .
.
5.Таблицы.
Таблица №1
Таблица №2
Таблица №3
6. Вычисления:
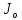 =
=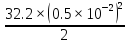 =4.25*
=4.25*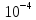
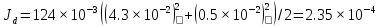
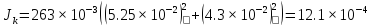
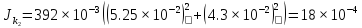
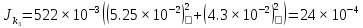
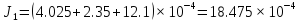
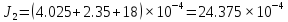
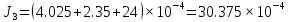
Санкт-Петербург
2012
