2_laba

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ

«ГОРНЫЙ»

Кафедра АТПП

Математические методы обработки данных

Лабораторная работа № 2

ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ ПО МЕТОДУ ГАИМЕНЬШИХ КВАДРАТОВ

Выполнил: студент гр.АПМ-13 ____ __________ / Озеров Б.А. /

^{(подпись) (Ф.И.О.)}

Проверил: доцент ­­­­­___________ / Иванов П.В. /

^{(подпись) (Ф.И.О.)}

Санкт-Петербург

2014 год

Цель работы: изучение практических приемов нахождения коэффициентов линейных и нелинейных регрессионных зависимостей и оценки точности аппроксимации с использованием программной среды MathCad.

Линейная аппроксимация.

Дано:

xi	Таблица данных y=f(x)
	0,1	0,5	1	2	4
8	1,53	1,69	1,77	1,86	1,95

Способы аппроксимации:

1) решение системы линейных уравнений, используя функцию line;

2) решение системы линейных уравнений с помощью конструкции Given – Find.

Выполнение задания:

1. решение системы линейных уравнений, используя функцию line.

Делаем матрицу данных нам величин, а именно x и y. Функция line просто вычисляет быстрым способом, находит не известные коэффициенты. Получаем искомые коэффициенты. Запись в программе MathCad представлена на рис.1

рис.1 решение системы линейных уравнений, используя функцию line

в программе MathCad

2. Конструкция Given – Find использует расчетную методичку, основанную на поиске корня вблизи точки начального приближения.

В блоке Given записывается система уравнений (неравенств), подлежащих решению. Система уравнений должна быть записана после или правее Given. Перед словом Given необходимо указывать начальные приближения для всех переменных. Признаком окончания системы служит Find.

Сначала задаем матрицу данных нам величин, а именно x и y. И задаем начальное приближение А и В, от которых будем начинать искать значения линейного уравнения Ах+В=y. Затем вводим служебное слово Given и после него записываем уравнение, используя знак жирное равно. И в конце написать функцию Find с неизвестными переменными в качестве параметра. Получаем искомые коэффициенты. Запись в программе MathCad представлена на рис.2

Используя метод наименьших квадратов, мы составляем уравнения, которые записываем после слова Given:

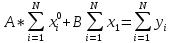
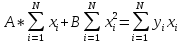
рис.2 решение системы линейных уравнений с помощью конструкции Given – Find

в программе MathCad

Вычислили коэффициенты аппроксимирующего полинома линейного уравнения двумя разными способами. Они совпали: (а=А, b=B)

Сделаем проверку пригодности найденного полинома изучаемого объекта, так называемую проверку на адекватность:

рис.3 проверка на адекватность при помощи коэффициента детерминации(R)

в программе MathCad

Построим график зависимости аппроксимирующего полинома(z) и экспериментальных данных(y,x) – рис.4.

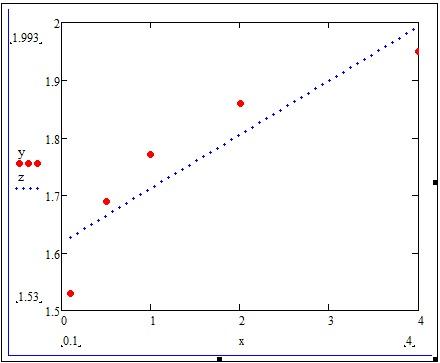
рис.4

Нелинейная аппроксимация.

Дано:

1. y=АВ^x

Решить систему нелинейной зависимости способом приведения зависимости к линейному виду.

2. y=a+bx+cx²

Решить систему нелинейной зависимости, использую функцию minimize.

Выполнение задания:

1. Зависимость y=АВ^x является нелинейной. Прологарифмировав это выражение, получим:

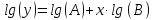
Сначала задаем матрицу данных нам величин, а именно x и y. Вводим обозначения z=lg(y), k=lg(A),s=lg(B). Таким образом задача сводится к линейной функции z=k+sx. Именно это и делают встроенные функции slope и intercept. Вводим обозначения переменных, которые нам нужно найти, а именно А и В. Находим значение неизвестного. Получаем искомые коэффициенты. Запись в программе MathCad представлена на рис.5

рис.5 способ решения системы нелинейной зависимости через приведение зависимости

к линейному виду в программе MathCad

2. Зависимость y=a+bx+cx² является нелинейной. Также найти коэффициенты аппроксимирующей функции можно осуществить с использование встроенной функции minimize, в которой реализуются алгоритмы оптимизации, основывающиеся на итерационных вычислениях и последовательном приближении к точке минимума.

Сначала задаем матрицу данных нам величин, а именно x и y. И задаем начальное приближение a, b и c, от которых будем начинать искать значения, данного нам нелинейного уравнения. Далее набираем функцию, которую необходимо оптимизировать. В данном случаем:

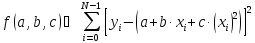
Задаем ограничения для искомых коэффициентов через Given. Вводим команду на минимизацию функции f(a,b,c). Получаем искомые коэффициенты. Запись в программе MathCad представлена на рис.6

рис.6 способ решения системы нелинейной зависимости, используя функцию minimize

в программе MathCad

Сделаем проверку пригодности найденного полинома изучаемого объекта, так называемую проверку на адекватность:

рис.7 проверка на адекватность при помощи коэффициента детерминации(R)

в программе MathCad

Построим график зависимости аппроксимирующего полинома(z) и экспериментальных данных(y,x) – рис.8.

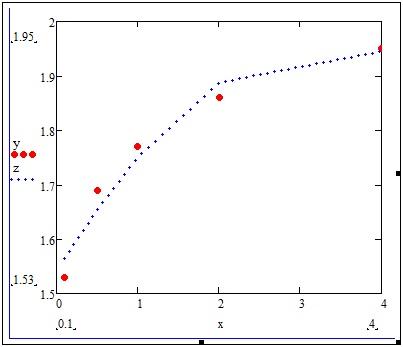
рис.8

Вывод: из двух предложенных видов зависимостей (линейная и нелинейная) нелинейная зависимость лучшим образом описывает экспериментальные данные.