Производные основных элементарных функций

№	Функция	Производная
1
2
3
4
5	(
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

6. Односторонние и бесконечные производные

Если функция задана на замкнутом интервале, то при определении производных на концах интервала приходится ограничиваться для левого конца значениями аргумента справа, а для правого конца - слева от него. Таким образом, возникает определение понятия односторонней производной. Может случиться также, что для некоторых внутренних точек существуют односторонние производные не равные между собой. Такие точки называютсяугловыми.

Если предел (Error: Reference source not found) равен , то говорят что в точкефункция имеет бесконечную производную. В этом случае угол наклона касательной к графику функции равен, т.е. сама касательная параллельна оси ординат. При этом односторонние производные могут иметь одинаковые или разные знаки.

Мусор.

1. Поскольку в точке существует производная, то приращениеможно представить в виде

,

где бесконечно малая величина при. Поскольку в точкесуществует производная, то приращениеможно представить в виде

,

где бесконечно малая величина при.

Подставляя последнее выражение в предшествующее к нему, получим

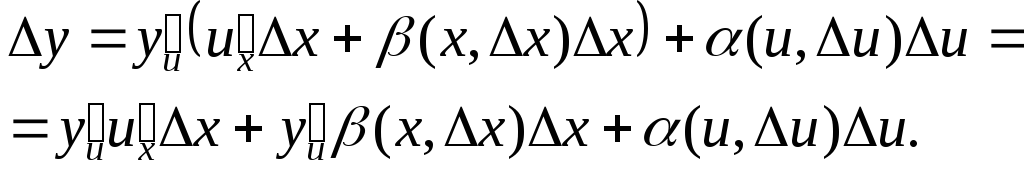
Разделив полученное соотношение на и перейдя к пределу приполучим

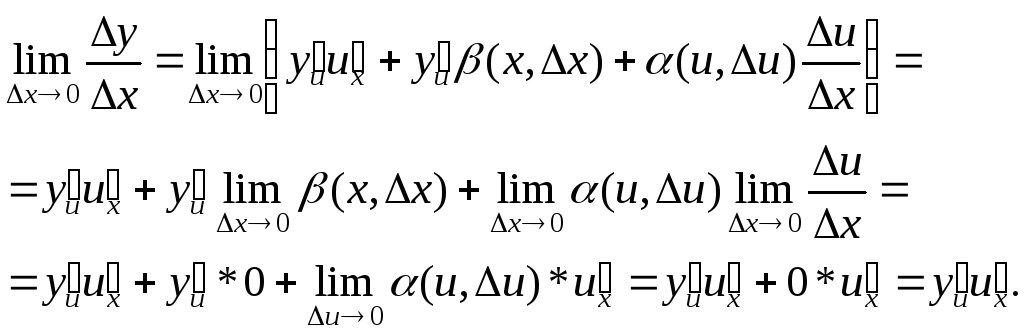
Текущий контроль.

1. Являются ли непрерывными основные элементарные функции?

2. Являются ли непрерывной сложная функция, составленная из непрерывных функций?

3. Каковы условия существования непрерывной обратной функции?

4. Сформулируйте 1-ю теорему Больцано-Коши.

5. Сформулируйте 2-ю теорему Больцано-Коши.

6. Сформулируйте 1-ю теорему Вейерштрасса.

7. Сформулируйте 2-ю теорему Вейерштрасса.

1Имена гиперболических синуса и косинуса представлены в обозначенияхMathcad.

2Имена гиперболических синуса и косинуса представлены в обозначенияхMathcad.

10