
- •Тема 4.1. Производная и дифференциал
- •1.3. Связь между существованием производной и непрерывностью функции
- •2. Геометрическое и механическое толкование производной
- •3. Производная суммы, произведения и частного от деления двух функций
- •4. Производная сложной и обратной функций.
- •5. Таблица производных
- •Производные основных элементарных функций
- •6. Односторонние и бесконечные производные
3. Производная суммы, произведения и частного от деления двух функций
Используем свойства предела для доказательства правил дифференцирования.
1.
![]()
![]() . (1)
. (1)
2.
![]()
![]() . (2)
. (2)
3.
![]()
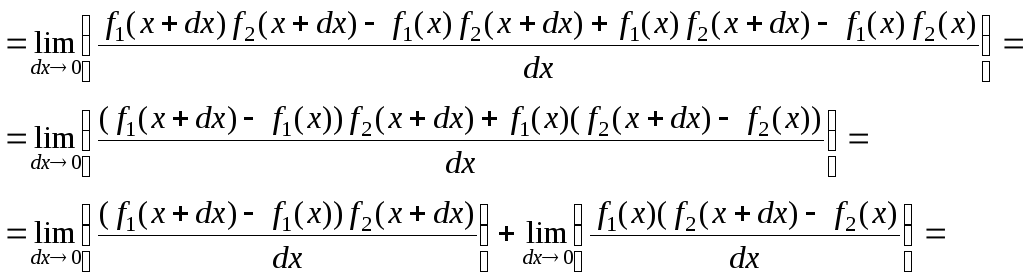
![]() (3)
(3)
4.
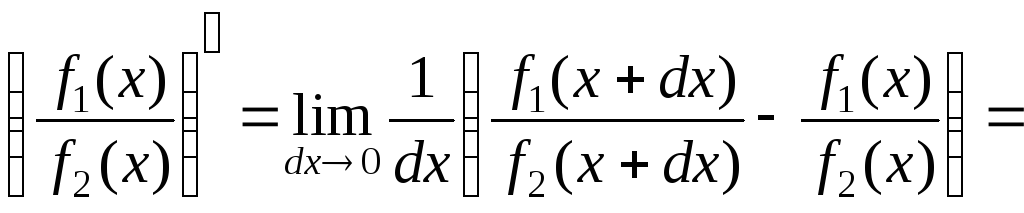
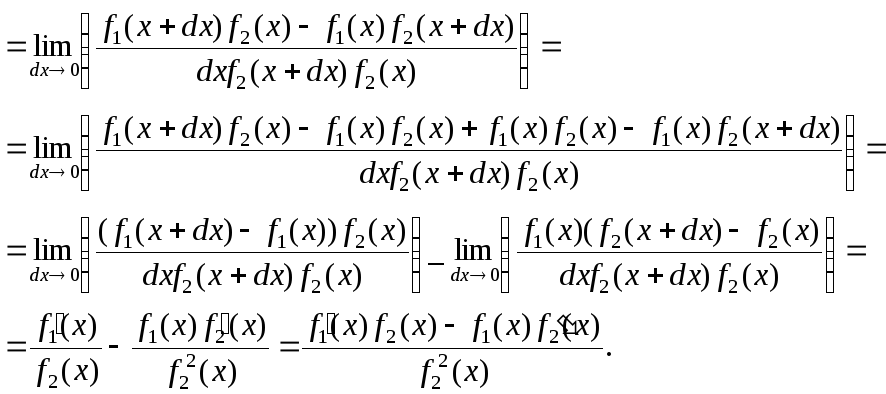 (4)
(4)
4. Производная сложной и обратной функций.
Пусть функция
![]() в некоторой окрестности точки
в некоторой окрестности точки![]() является непрерывной, монотонной, а в
самой точке
является непрерывной, монотонной, а в
самой точке![]() - дифференцируемой. Тогда по теореме о
непрерывных функциях она имеет обратную
- дифференцируемой. Тогда по теореме о
непрерывных функциях она имеет обратную![]() .
Найдем связь между производными прямой
и обратной функций
.
Найдем связь между производными прямой
и обратной функций
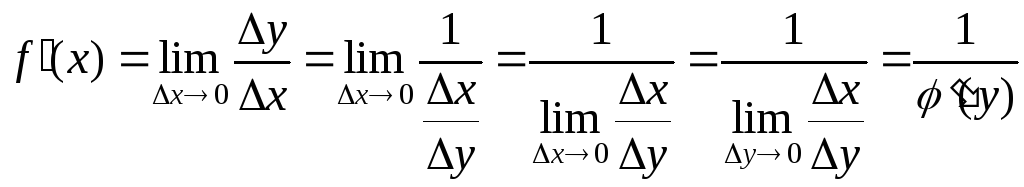 . (1)
. (1)
Формулу (1) следует
понимать так, что производные в ее левой
и правой части вычисляются при значениях
аргументов, связанных между собой
соотношениями
![]() или
или![]() .
.
Определение.Сложнойназывается функция, которая зависит от своего аргумента, таким образом, что эту зависимость можно представить посредством как минимум одного промежуточного аргумента.
Например, пусть
![]() и
и![]() .
Тогда
.
Тогда![]() - сложная функция с промежуточным
аргументом
- сложная функция с промежуточным
аргументом![]() и независимым аргументом
и независимым аргументом![]() .
.
Теорема.
Если функция![]() имеет производную
имеет производную![]() в точке
в точке![]() ,
а функция
,
а функция![]() имеет производную
имеет производную![]() в точке
в точке![]() ,
соответствующей точке
,
соответствующей точке![]() ,
то сложная функция
,
то сложная функция![]() имеет производную
имеет производную![]() в точке
в точке![]() ,
которая находится по формуле
,
которая находится по формуле
![]() . (2)
. (2)
Доказательство
В окрестности
точки
![]() дадим приращение
дадим приращение![]() аргументу
аргументу![]() .
Тогда промежуточный аргумент
.
Тогда промежуточный аргумент![]() получит приращение
получит приращение![]() ,
а функция
,
а функция![]() - приращение
- приращение![]() .
.
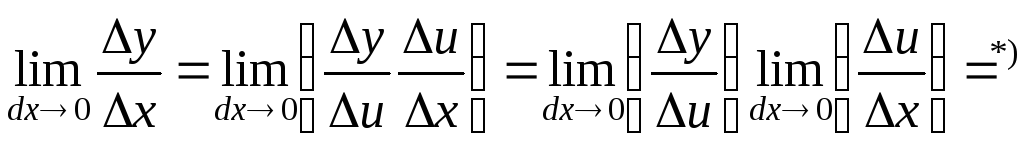 .
.
Поскольку в силу
существования производной
![]() функция
функция![]() является непрерывной в рассматриваемой
точке, то при
является непрерывной в рассматриваемой
точке, то при![]() следует, что
следует, что![]() .
Тогда продолжая выкладки, получаем
.
Тогда продолжая выкладки, получаем
![]() .
.
5. Таблица производных
Получим сейчас формулы для дифференцирования основных элементарных функций. Знание этих формул совместно с ранее полученными правилами дифференцирования позволит нам выполнять дифференцирование элементарных функций.
Пусть
 .
Применяя формулу (1) получим
.
Применяя формулу (1) получим
![]() . (1)
. (1)
Пусть
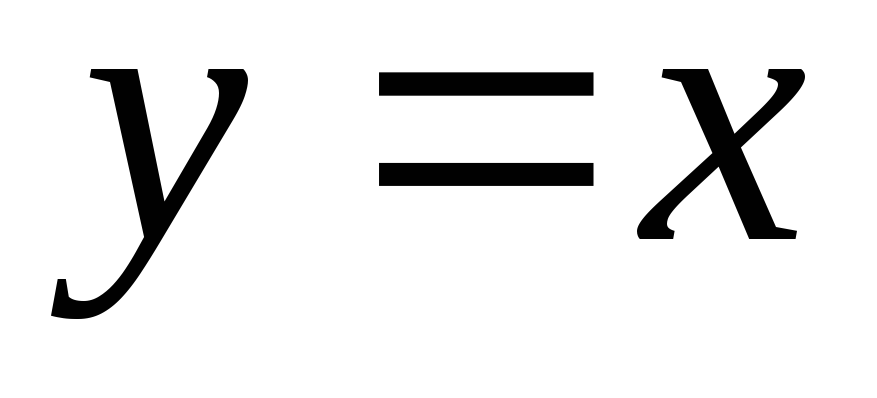 .
Тогда
.
Тогда
![]() . (2)
. (2)
3. Получим производную
степенной функции
![]() с вещественным показателем степени
с вещественным показателем степени![]() .
При этом воспользуемся таблицей
эквивалентных бесконечно малых величин.
.
При этом воспользуемся таблицей
эквивалентных бесконечно малых величин.
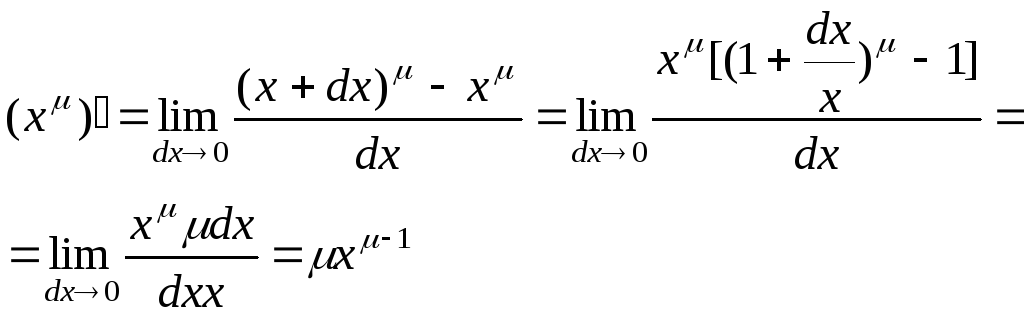 . (3)
. (3)
В частном случае,
когда
![]() = целое число
= целое число
![]() . (4)
. (4)
4. Для получения
формулы дифференцирования показательной
функции
![]() (
(![]() также воспользуемся таблицей эквивалентных
бесконечно малых величин
также воспользуемся таблицей эквивалентных
бесконечно малых величин
![]() . (5)
. (5)
В частном случае,
когда
![]()
![]() . (6)
. (6)
5. Для получения
формулы дифференцирования логарифмической
функции
![]() (
(![]() также воспользуемся таблицей эквивалентных
бесконечно малых величин. В результате
получим
также воспользуемся таблицей эквивалентных
бесконечно малых величин. В результате
получим
 . (1)
. (1)
В частном случае,
когда
![]()
![]() . (2)
. (2)
Перейдем теперь к вычислению производных тригонометрических функций.
6. Найдем производную
функции
![]() .
Пользуясь таблицей эквивалентных
бесконечно малых величин, получим
.
Пользуясь таблицей эквивалентных
бесконечно малых величин, получим
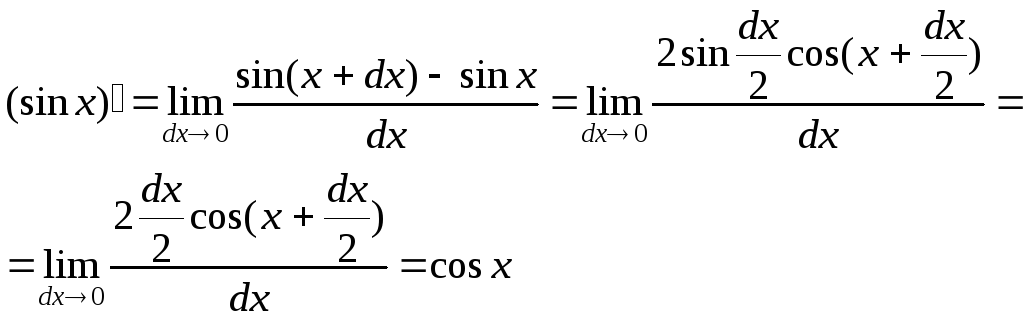 . (9)
. (9)
7. Найдем производную
функции
![]() .
Пользуясь таблицей эквивалентных
бесконечно малых величин, получим
.
Пользуясь таблицей эквивалентных
бесконечно малых величин, получим
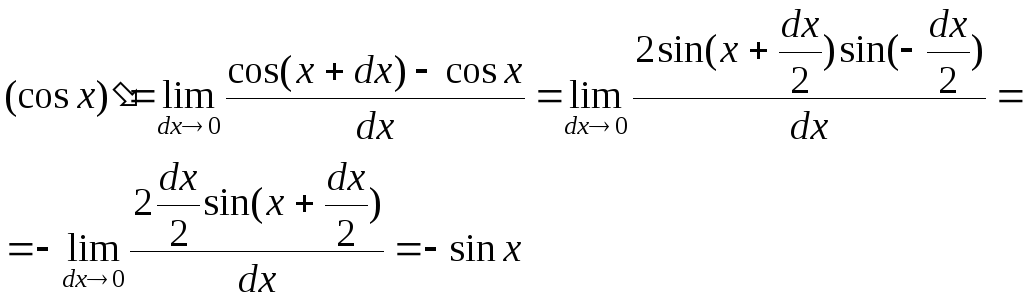 . (10)
. (10)
8. Найдем производную
функции
![]() .
Пользуясь правилами дифференцирования,
получим
.
Пользуясь правилами дифференцирования,
получим
![]() . (11)
. (11)
9. Найдем производную
функции
![]() .
Пользуясь правилом дифференцирования
частного от деления двух функций, получим
.
Пользуясь правилом дифференцирования
частного от деления двух функций, получим
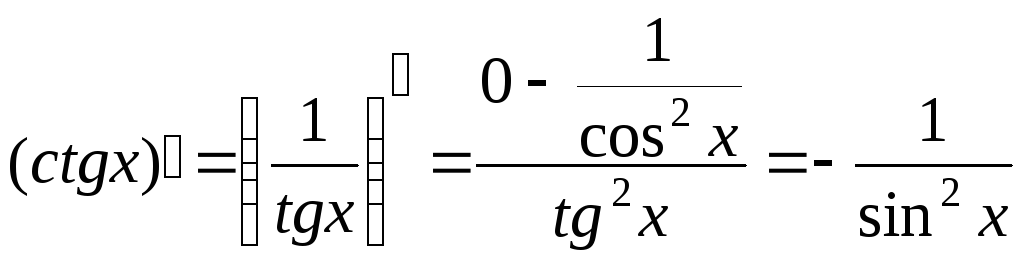 . (12)
. (12)
10. Найдем производную
функции
![]() ,
где
,
где![]() ,
а
,
а![]() .
Очевидно
.
Очевидно![]() ,
тогда пользуясь формулами (3.1) и (9),
получим
,
тогда пользуясь формулами (3.1) и (9),
получим
![]() . (13)
. (13)
Здесь было
использовано свойство функции
![]() на промежутке
на промежутке![]() .
.
11. Найдем производную
функции
![]() ,
где
,
где![]() ,
а
,
а![]() .
Очевидно
.
Очевидно![]() ,
тогда пользуясь формулами (3.1) и (10),
получим
,
тогда пользуясь формулами (3.1) и (10),
получим
![]() . (14)
. (14)
Здесь было
использовано свойство функции
![]() на промежутке
на промежутке![]() .
.
12. Найдем производную
функции
![]() ,
где
,
где![]() ,
а
,
а![]() .
Очевидно
.
Очевидно![]() ,
тогда пользуясь формулами (3.1) и (11),
получим
,
тогда пользуясь формулами (3.1) и (11),
получим
![]() . (15)
. (15)
13. Найдем производную
функции
![]() ,
где
,
где![]() ,
а
,
а![]() .
Очевидно
.
Очевидно![]() ,
тогда пользуясь формулами (3.1) и (12),
получим
,
тогда пользуясь формулами (3.1) и (12),
получим
![]() . (16)
. (16)
14. Так как гиперболический синус определяется соотношением
![]() ,
то
,
то
![]() . (17)
. (17)
15. Так как гиперболический косинус определяется соотношением
![]() ,
то
,
то
![]() . (18)
. (18)
Графики гиперболического синуса и косинуса представлены на рис. 1.
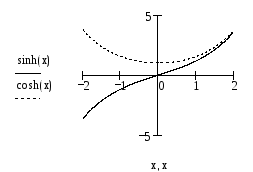
Рис. 1. Синус и косинус гиперболические1
16. Так как гиперболический тангенс определяется соотношением
![]() ,
то
,
то
![]() . (19)
. (19)
17. Так как гиперболический котангенс определяется соотношением
![]() ,
то
,
то
![]() . (20)
Графики гиперболического тангенса и
котангенса представлены на рис. 2.
. (20)
Графики гиперболического тангенса и
котангенса представлены на рис. 2.
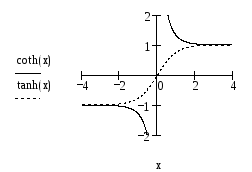
Рис. 2. Тангенс и котангенс гиперболические2
Результаты вычисления производных представлены в таблице.
Таблица
