
- •Тема 4.1. Производная и дифференциал
- •1.3. Связь между существованием производной и непрерывностью функции
- •2. Геометрическое и механическое толкование производной
- •3. Производная суммы, произведения и частного от деления двух функций
- •4. Производная сложной и обратной функций.
- •5. Таблица производных
- •Производные основных элементарных функций
- •6. Односторонние и бесконечные производные
Тема 4.1. Производная и дифференциал
Тема 4.1. Производная и дифференциал 1
1. Дифференцируемость функции в точке и в области 1
1.1. Производная функции 1
1.2. Дифференциал 1
1.3. Связь между существованием производной и непрерывностью функции 2
2. Геометрическое и механическое толкование производной 3
3. Производная суммы, произведения и частного от деления двух функций 3
4. Производная сложной и обратной функций. 4
5. Таблица производных 5
6. Односторонние и бесконечные производные 9
1. Дифференцируемость функции в точке и в области
1.1. Производная функции
Определение.
Пусть функция![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки![]() .
Рассмотрим предел
.
Рассмотрим предел
![]() .
.
Если он существует,
то называется производнойфункции![]() в точке
в точке![]() .
Производная обозначается одним из
следующих способов:
.
Производная обозначается одним из
следующих способов:
![]() . (1)
. (1)
Используется также другой вариант записи формулы (1). Если ввести обозначения:
![]() , (2)
, (2)
то формула (1) может быть записана в виде
![]() . (3)
. (3)
1.2. Дифференциал
Определение.
Дифференциалом функции![]() в точке
в точке![]() называется выражение
называется выражение
![]() . (1)
. (1)
Если рассматривать независимую переменную как функцию самой себя, то ее дифференциал представляется выражением
![]() (2)
(2)
и определение дифференциала поэтому записывают в виде
![]() (3)
(3)
В соответствии с
определением дифференциал можно
рассматривать как функцию двух независимых
аргументов
![]() и
и![]() ,
причем по второму аргументу эта функция
является линейной.
,
причем по второму аргументу эта функция
является линейной.
Равенство (3)
позволяет рассматривать вариант
обозначения производной в виде
![]() как частное от деления дифференциала
функции на дифференциал аргумента.
как частное от деления дифференциала
функции на дифференциал аргумента.
Между приращением
функции и ее дифференциалом существует
тесная связь. Действительно, по свойству
предела (1.1.1) отношение
![]() отличается от своего предела
отличается от своего предела![]() на бесконечно малую величину
на бесконечно малую величину![]() при
при![]() ,
т.е.
,
т.е.
![]() .
.
Умножим последнее
равенство на
![]() и с учетом (3) получим
и с учетом (3) получим
![]() . (4)
. (4)
Таким образом,
приращение функции есть сумма двух
слагаемых: дифференциала, являющегося
линейной функцией приращения аргумента,
и, вообще говоря, нелинейной относительно
приращения аргумента части. Покажем,
что эта нелинейная часть является
бесконечно малой более высокого порядка
малости по сравнению с дифференциалом
при
![]() ,
если производная не равна нулю.
Действительно,
,
если производная не равна нулю.
Действительно,
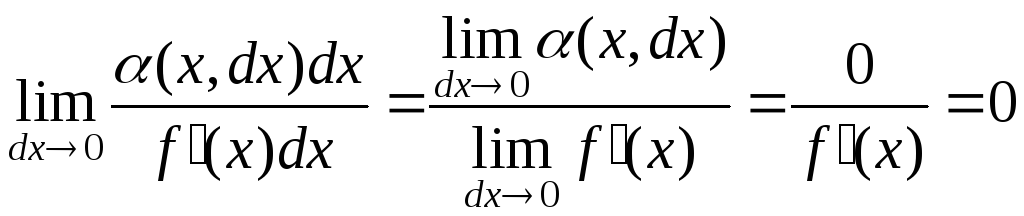 . (5)
. (5)
Следовательно,
слагаемое
![]() является бесконечно малой величиной
более высокого порядка малости, чем
дифференциал
является бесконечно малой величиной
более высокого порядка малости, чем
дифференциал![]() .
Это дает основание называть дифференциал
главной линейной частью приращения
функции. Из формулы (5) следует, что
приращение функции и дифференциал
являются эквивалентными бесконечно
малыми величинами. Действительно,
разделив формулу (4) на
.
Это дает основание называть дифференциал
главной линейной частью приращения
функции. Из формулы (5) следует, что
приращение функции и дифференциал
являются эквивалентными бесконечно
малыми величинами. Действительно,
разделив формулу (4) на![]() с учетом соотношения (5) получим
с учетом соотношения (5) получим
![]() . (6)
. (6)
1.3. Связь между существованием производной и непрерывностью функции
Пусть функция
![]() имеет производную в точке
имеет производную в точке![]() .
Тогда выполняется соотношение (1.2.4),
т.е.
.
Тогда выполняется соотношение (1.2.4),
т.е.
![]() . (1)
. (1)
После переноса
![]() в правую часть соотношения и, переходя
к пределу, получим
в правую часть соотношения и, переходя
к пределу, получим
![]() . (2)
. (2)
Соотношение (2)
обозначает непрерывность функции в
точке
![]() .
Таким образом, из дифференцируемости
следует непрерывность функции.
.
Таким образом, из дифференцируемости
следует непрерывность функции.
2. Геометрическое и механическое толкование производной
Рассмотрим поведение
произвольной функции
![]() в окрестности точки
в окрестности точки![]() .
Проведем прямую, проходящую через точку
с координатами
.
Проведем прямую, проходящую через точку
с координатами![]() и пересекающую график функции
и пересекающую график функции![]() в соседней точке с координатами
в соседней точке с координатами![]() .
Эта прямая называется секущей.
.
Эта прямая называется секущей.
Тангенс угла
![]() между секущей и положительным направлением
оси абсцисс определяется соотношением
между секущей и положительным направлением
оси абсцисс определяется соотношением
![]() . (1)
. (1)
При
![]() секущая переходит в касательную, а угол
секущая переходит в касательную, а угол![]() переходит в угол
переходит в угол![]() наклона касательной к положительному
направлению оси абсцисс
наклона касательной к положительному
направлению оси абсцисс
![]() . (2)
. (2)
Соотношение (2) составляет так называемый геометрический смысл производной.
Соотношение (2)
позволяет построить уравнение касательной
к графику функции
![]() в точке
в точке![]() .
Уравнение прямой в форме с угловым
коэффициентом имеет вид
.
Уравнение прямой в форме с угловым
коэффициентом имеет вид
![]() .
.
Известно, что
угловой коэффициент
![]() равен тангенсу угла наклона касательной
к графику функции, т.е.
равен тангенсу угла наклона касательной
к графику функции, т.е.![]() ,
а уравнение прямой проходящей через
точку с координатами
,
а уравнение прямой проходящей через
точку с координатами![]() имеет
вид
имеет
вид
![]() . (3)
. (3)
Легко получить
также уравнение перпендикуляра к кривой
в точке
![]() .
Если угол наклона касательной к кривой
считать равным
.
Если угол наклона касательной к кривой
считать равным![]() ,
то угол наклона перпендикуляра будет
равен
,
то угол наклона перпендикуляра будет
равен![]() .
Угловой коэффициент наклона перпендикуляра
получается из следующей цепочки
соотношений
.
Угловой коэффициент наклона перпендикуляра
получается из следующей цепочки
соотношений
![]() .
.
Заменяя в уравнении (3) угловой коэффициент, получим уравнение перпендикуляра в виде
![]() . (4)
. (4)
