
- •Введение
- •Электромагнетизм
- •1. Электростатика
- •1.1. Электрический заряд
- •1.2. Закон Кулона
- •1.3. Напряженность электростатического поля
- •1.4. Поток вектора напряженности. Теорема Гаусса
- •1.5. Потенциал. Разность потенциалов
- •1.6. Диэлектрики в электрическом поле
- •1.7. Проводники в электрическом поле
- •1.8. Электрическая емкость. Конденсаторы
- •Примеры решения задач
- •Контрольные вопросы и задания
- •2. Законы постоянного тока
- •2.1. Сила тока. Закон Ома
- •2.2. Последовательное и параллельное соединение проводников
- •2.3. Правила Кирхгофа
- •2.4. Действие электрического тока
- •Примеры решения задач
- •Контрольные вопросы и задания
- •3. Магнетизм
- •3.1. Магнитное поле. Опыт Ампера
- •3.2. Магнитная индукция
- •3.3. Закон Био-Савара-Лапласа
- •3.4. Силы Ампера и Лоренца
- •3.5. Магнитный поток. Теорема Гаусса и закон полного тока
- •3.6. Явление электромагнитной индукции
- •3.7. Явление самоиндукции
- •3.8. Энергия магнитного поля
- •Примеры решения задач
- •Контрольные вопросы и задания
- •4. Электромагнитные колебания
- •Примеры решения задач
- •Контрольные вопросы и задания
- •5. Уравнения Максвелла
- •5.1. Ток смещения
- •5.2. Уравнения Максвелла в интегральной форме
- •5.3. Уравнения Максвелла в дифференциальной форме
- •5.4. Свойства уравнений Максвелла
- •Примеры решения задач Задача 5.1.
- •Контрольные вопросы и задания
- •6.Основные понятия, законы и формулы
- •10. Температурная зависимость сопротивления
- •32. Мощность в цепи переменного тока
- •33.Уравнения Максвелла в интегральной форме
- •7. Задачи для самостоятельного решения
- •8. Пример научной проблемы и технического использования электростатики
- •8.1. Влияние дискретности распеделения заряда на электростатическое поле и его силовые характеристики
- •Справочные материалы
- •Удельное сопротивление, температурный коэффициент сопротивления (при 20,0)
- •Относительные диэлектрические проницаемости
- •Библиографический список учебной и научной литературы
- •Заключение
- •Предметный указатель
- •Содержание
1.2. Закон Кулона
Взаимодействие двух неподвижных точечных зарядов, находящихся в вакууме, определяется законом Кулона: сила взаимодействия F пропорциональна зарядам q1 и q2, и обратно пропорциональна квадрату расстояния r между ними:
![]() ,
,
где
![]() ‑ единичный вектор, направленный
вдоль линии, соединяющей заряды,
‑ единичный вектор, направленный
вдоль линии, соединяющей заряды,
![]() Ф/м
‑ электрическая
постоянная;
Ф/м
‑ электрическая
постоянная;
![]() .
.
Сила Кулона направлена по прямой, соединяющей взаимодействующие заряды, т. е. является центральной, и соответствует притяжению (F < 0) в случае разноименных зарядов и отталкиванию (F > 0) в случае одноименных зарядов. В соответствии с третьим законом Ньютона для взаимодействия неподвижных зарядов выполняется равенство (рис. 1.2):
![]() .
.
Этот закон был открыт экспериментально в 1785 г. Шарлем Кулоном с помощью крутильных весов (рис. 1.1).

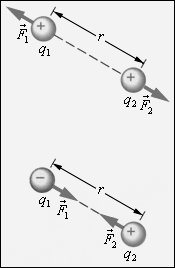
Рис. 1.1. Прибор КулонаРис. 1.2. Сила Кулона
Если взаимодействующие заряды находятся в изотропной непроводящей среде, то кулоновская сила
![]() ,
,
где
![]() –диэлектрическая
проницаемость среды, показывающая
во сколько
раз сила взаимодействия F
между зарядами
в данной среде меньше их силы взаимодействия
F0
в вакууме:
–диэлектрическая
проницаемость среды, показывающая
во сколько
раз сила взаимодействия F
между зарядами
в данной среде меньше их силы взаимодействия
F0
в вакууме:
![]() .
.
Диэлектрическая
проницаемость вакуума и большинства
газообразных сред равна, или близка
единице:
![]() .
.
1.3. Напряженность электростатического поля
При рассмотрении взаимодействия заряженных тел и точечных зарядов, возникает вопрос, почему появляются силы, действующие на заряды, находящиеся иногда на очень большом расстоянии и разделенных пустотой (вакуумом)? Для ответа на этот вопрос следует предположить наличие между зарядами какого-то физического агента, осуществляющего передачу этого взаимодействия. В 1830-х годах М. Фарадей разработал теорию близкодействия, из которой вытекало понятие электромагнитного поля.
Согласно этой теории любой заряд является источником электромагнитного поля, распространяющегося в пространстве со скоростью света. В случае неподвижных зарядов такое поле называется электростатическим. Его основное свойство заключается в том, что на всякий заряд, помещенный в это поле, действует сила. Таким образом, можно считать, что не заряды взаимодействуют непосредственно друг с другом, а каждый из неподвижных зарядов создает в пространстве электростатическое поле, которое и действует на другой заряд. Электростатическое поле описывается двумя величинами: потенциалом и напряженностью.
Напряженность
электрического поля является силовой
векторной характеристикой электрического
поля и равна силе
![]() ,
действующей напробный
положительный
заряд
,
действующей напробный
положительный
заряд
![]() ,
помещенный в данную точку поля,
деленной на величину этого заряда
(пробный заряд должен обладать достаточно
малыми размерами, чтобы не искажать
измеряемое поле):
,
помещенный в данную точку поля,
деленной на величину этого заряда
(пробный заряд должен обладать достаточно
малыми размерами, чтобы не искажать
измеряемое поле):
![]() ,
В/м.
,
В/м.
Направление
вектора
![]() совпадает с направлением силы
совпадает с направлением силы![]() ,
действующей на положительный заряд.
,
действующей на положительный заряд.
Графически
электростатическое поле изображают с
помощью линий
напряженности
(силовых
линий) –
линий, касательные к которым в каждой
точке совпадают с направлением вектора
![]() (рис. 1.3). Для силовых линий выбирается
направление, совпадающее с направлением
вектора напряженности, при этом такие
линии никогда не пересекаются. В случае
однородного поля (когда вектор
напряженности в любой точке пространства
постоянен по модулю и направлению) линии
напряженности параллельны вектору
напряженности.
(рис. 1.3). Для силовых линий выбирается
направление, совпадающее с направлением
вектора напряженности, при этом такие
линии никогда не пересекаются. В случае
однородного поля (когда вектор
напряженности в любой точке пространства
постоянен по модулю и направлению) линии
напряженности параллельны вектору
напряженности.
С
тем чтобы графически охарактеризовать
не только направление, но и модуль
напряженности электростатического
поля, силовые линии проводят с определенной
густотой:
число линий напряженности пронизывающих
единицу площади поверхности,
перпендикулярную линиям напряженности,
должно быть равно модулю вектора
напряженности:
![]() (рис. 1.3).
(рис. 1.3).

Рис. 1.3. Силовые линии электрического неоднородного поля
Силовые линии кулоновских полей положительных и отрицательных точечных зарядов изображены на рис. 1.4.
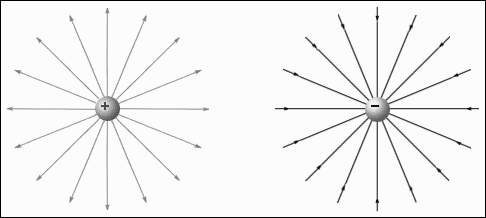
Рис. 1.4. Силовые линии полей точечных зарядов
Для электростатического поля справедлив принцип суперпозиции: напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности:
![]() ,
,
где
![]() – напряженность электрического поля,
созданного
– напряженность электрического поля,
созданного![]() -м
зарядом в данной точке. Принцип
суперпозиции позволяет вычислять
напряженность поля любой системы
неподвижных зарядов, представив его в
виде совокупности точечных зарядов.
-м
зарядом в данной точке. Принцип
суперпозиции позволяет вычислять
напряженность поля любой системы
неподвижных зарядов, представив его в
виде совокупности точечных зарядов.
В качестве примера применения принципа суперпозиции полей на рис. 1.5 изображена картина силовых линий поля электрического диполя – системы из двух одинаковых по модулю зарядов разного знака q и –q, расположенных на некотором расстоянии l.

Рис. 1.5. Силовые линии поля электрического диполя
