3.3. Закон Био-Савара-Лапласа

Закон Био–Савара–Лапласа позволяет рассчитать индукцию магнитного поля, создаваемого проводником с током, в любой точке пространства (рис. 3.2):

; ,

где – сила тока;– элемент длины провода (векторсовпадает по направлению с током);– радиус-вектор, проведенный от элементак точке наблюдения.

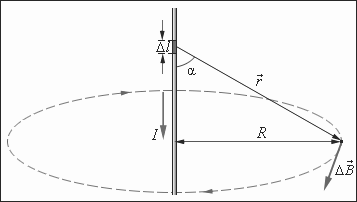
Рис. 3.2. Закон Био-Савара-Лапласа

Индукция магнитного поля бесконечно длинного прямого проводника с током (Рис. 3.3)

,

где – расстояние от точки наблюдения до оси проводника;– магнитная проницаемость среды, в которой находится проводник.

Рис. 3.3. Магнитное поле прямолинейного проводника с током

Индукция магнитного поля прямого проводника конечной длины

,

где – расстояние от точки наблюдения до прямой, на которой лежит проводник;– угол между проводником и радиус-вектором, проведенным из начала проводника в точку наблюдения;– угол между проводником и радиусом-вектором, проведенным из конца проводника в точку наблюдения. При симметричном расположении концов проводника относительно точки, в которой определяется магнитная индукция, , и тогда

.

Индукция магнитного поля движущегося в вакууме точечного заряда

,

где – электрический заряд;– постоянная нерелятивистская скорость;– радиус-вектор, проведенный от заряда к точке наблюдения.

Индукция магнитного поля в центре кругового витка с током

,

где – радиус кругового витка;– магнитный момент витка.

Индукция магнитного поля на оси кругового витка с током

,

где – расстояние от плоскости витка до точки наблюдения, которая находится на оси кругового витка;– радиус витка.

Индукция магнитного поля в центре дуги окружности

,

где – длина дуги;– радиус дуги.

Индукция магнитного поля внутри длинного соленоида на его оси (рис. 3.4)

,

где – магнитная проницаемость сердечника;– число витков на единице длины соленоида.

Рис. 3.4. Магнитное поле внутри соленоида

Рис. 3.5. Линии магнитной индукции полей постоянного магнита

и катушки с током

Индукция магнитного поля на оси тороида (рис. 3.6)

,

где – магнитная проницаемость сердечника;– число витков, намотанных на тороид;– радиус центральной линии тороида.

Рис. 3.6. Поле тороида

3.4. Силы Ампера и Лоренца

Закон Ампера определяет силу, действующую на проводник с током, помещенный в магнитное поле:

; ,

где – сила тока;– элемент длины провода (векторсовпадает по направлению с током);– длина проводника. Сила Ампера перпендикулярна направлению тока и направлению вектора магнитной индукции.

Если прямолинейный проводник длиной находится в однородном поле, то модуль силы Ампера определяется выражением (рис. 3.7):

.

Рис. 3.7. Правило левой руки и правило буравчика для определения направления силы Ампера

Сила Лоренца (полная электромагнитная сила, действующая на заряженную частицу в электрическом и магнитном полях)

,

где – электрический заряд;– напряженность электрического поля;– скорость частицы;– индукция магнитного поля.

Только в магнитном поле на движущуюся заряженную частицудействует магнитная составляющая силы Лоренца (рис. 3.8)

.

Магнитная составляющая силы Лоренца перпендикулярна вектору скорости и вектору магнитной индукции. Она не изменяет величины скорости, а изменяет только ее направление, следовательно, работы не совершает.

Рис. 3.8. Сила Лоренца

Если частица влетает в магнитное поле под углом к силовым линиям, то она равномерно движется в магнитном поле по окружности радиусом и периодом обращения:

; ,

где – масса частицы.

Если заряженная частица влетает в однородное магнитное поле под углом , то она движется по винтовой линии (рис. 3.9).

Рис. 3.9. Движение по винтовой линии заряженной частицы в магнитном поле

Рис. 3.10. Заряженные частицы не выходят за пределы магнитной «бутылки». Поле может быть создано с помощью двух круглых витков с током

Отношение магнитного момента к механическомуL (моменту импульса) заряженной частицы, движущейся по круговой орбите,

,

где ‑ заряд частицы; т ‑ масса частицы.