4. Результаты эксперимента.

Для математического моделирования массообмена в реакторе анаэробного сбраживания были использованы следующие исходные данные.

Таблица

4. Описание математической модели массообмена процесса анаэробного сбраживания многокомпонентного органического сырья и анализ полученных результатов

Рассматривается реактор с рубашкой и мешалкой, внутри которого осуществляется процесс анаэробного сбраживания органической массы (рисунок 1)

Рисунок 1 - Реактор для получения биогаза:

1 - корпус реактора, 2 - рубашка, 3 - мешалка.

Водный раствор органической массы периодически загружается в реактор с одновременным отводом продуктов разложения. Образующийся биогаз отводится через верхний штуцер. Рабочая среда при работе биогазового реактора расслаивается на три области:

• суспензия, состоящая из твердых частиц органической природы, взвешенных в слое воды;

• светлый слой, состоящий, преимущественно, из воды;

• масляный слой.

После первоначальной загрузки реакционная среда нагревается теплоносителем, циркулирующим в рубашке, до температуры 37^оС. При такой температуре процесс анаэробного сбраживания протекает наиболее интенсивно. В результате жизнедеятельности бактерий вырабатывается биогаз, состоящий на 70% из метана и примерно на 30% из углекислого газа с теплотой сгорания примерно 25-29 МДж/нм³. Производительность биореактора при оптимальном режиме составляет 2-7 м³/сутки на 1 м³ реакционной смеси.

Эффективность работы биореактора определяется многими параметрами [13], важнейшими из которых являются температура, интенсивность перемешивания, показатель рН и др.

Субстрат подается в реактор в непрерывном режиме или мелкими порциями, а прореагировавшее сырье выводится из реактора.

Газовые пузыри зарождаются, преимущественно, в нижней части реактора на поверхности твердых органических частиц субстрата и стенках. При достижении радиуса отрыва R_о газовый пузырь отрывается от твердой поверхности и всплывает. По мере движения его радиус увеличивается из-за массообмена с жидкой фазой. Закон изменения радиуса пузыря и скорость всплытия существенно влияют на процессы тепломассообмена и производительность реактора.

Радиус пузыря, при котором происходит его отрыв от твердой поверхности, определяется соотношением [14]:

, (5.1.1)

где– краевой угол в момент отрыва;

σ

ρ_ж, ρ_г- плотности жидкости и газа.

После отрыва газовый пузырь всплывает. В процессе всплытия количество газа в нем увеличивается пропорционально коэффициенту массоотдачи и площади поверхности газового пузыря.

Закон изменения объема газового пузыря определяется соотношением:

, (5.1.2)

β – коэффициент массоотдачи от жидкости;

R_г – газовая постоянная газа;

Т – абсолютная температура;

∆Р_г– перепад парциальных давлений газа;

– плотность газа;

S – площадь поверхности пузыря;

С учетом выражений для объема газового пузыря

(5.1.3)

и площади его поверхности

(5.1.4)

из (2.2) получим

(5.1.5)

Коэффициент массоотдачи к поверхности пузыря определяется уравнением Буссинеска [15]

, (5.1.6)

где – число Шервуда;

– число Рейнольдса;

- число Шмидта;

- диаметр пузыря;

D – коэффициент диффузии биогаза в жидкости;

V_п – относительная скорость пузыря в жидкости.

С учетом (5.1.6) преобразуем уравнение (5.1.5) к виду:

где - коэффициент пропорциональности, зависящий от режимных параметров.

Относительная скорость газового пузыря в начальный период движения зависит от его радиуса [15]:

(5.1.8)

При достижении максимальной скорости, скорость газового пузыря остается неизменной независимо от его радиуса R.

, (5.1.9)

где

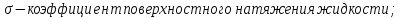
– коэффициент гидравлического сопротивления газового пузыря.

Из выражения (5.1.7) получим величину радиуса R_ж, при котором достигается максимальная относительная скорость пузыря :

. (5.1.10)

С учетом выражений (5.1.8), (5.1.9) интегрируем дифференциальное уравнение (5.1.7):

при R<R_ж

, (5.1.11)

где ;

при R

, (5.1.12)

– время, за которое газовый пузырь достигает максимальной скорости , находится по формуле:

Коэффициент поверхностного натяжения и кинематической вязкости реакционной смеси определяется соотношением [16]:

(5.1.14)

, (5.1.15)

где СВ – доля сухих веществ в сырье, поступающем в реактор в процентах;

Т_р- абсолютная температура в реакторе.

Коэффициент пропорциональности определяется по радиусу газового пузыря на выходе из слоя реакционной массы:

, (5.1.16)

откуда следует:

(5.1.17).

Моделирование процессов теплообмена в биогазовом реакторе.

Поскольку теплофизические свойства жидкости в слоях 1,2,3 существенно отличаются, коэффициенты теплопередачи рассчитываются для каждого слоя отдельно, а затем определяется средний коэффициент теплоотдачи.

1 слой

Плотность среды:

, (5.1.18)

где Ф – объемная доля твердых взвешенных частиц;

– плотность твердых частиц;

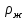– плотность жидкости.

Динамическая вязкость среды [4]:

Теплоемкость и теплопроводность среды:

, (5.1.20)

, (5.1.21)

гдес_т, с_ж– теплоемкости твердых частиц и жидкости;

λ_т, λ_ж– теплопроводности твердых частиц и жидкости;

– массовая доля твердых частиц, находится по формуле:

Число Рейнольдса для мешалки:

где 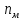– частота вращения мешалки, 1/с;

– диаметр мешалки, м;

– кинематический коэффициент вязкости.

Число Нуссельта:

, (5.1.24)

где –

Коэффициент теплоотдачи:

Аналогично определяются коэффициенты теплоотдачи для слоев 2,3. Критериальная формула для числа Нуссельта в этих случаях имеет вид [14]:

, (5.1.26)

где – динамическая вязкость жидкости при температуре стенки.

Средний коэффициент теплоотдачи:

(5.1.27)

Определим закон изменения температуры реакционной смеси от времени из уравнения теплового баланса:

, (5.1.28)

где – общая масса реакционной смеси, находится по формуле:

– общий объем реакционной смеси, находится по формуле:

– коэффициент теплопередачи от теплоносителя к реакционной смеси, находится по формуле:

– средняя температура теплоносителя в рубашке;

- начальная температура сырья, подаваемого в реактор;

– температура наружного воздуха.

Разделив (5.1.28) на получим:

, (5.1.32)

где

, (5.1.33)

, (5.1.34)

, (5.1.35)

. (5.1.36)

Преобразуем (5.1.32) к виду:

, (5.1.37)

где (5.1.38)

Интегрируя (5.1.37) по времени при начальном условии

(5.1.39)

получим:

, (5.1.40)

где – температура реакционной смеси, при .

В качестве исходных данных для математической модели берутся значения:

Массовая доля метана в биогазе ;

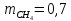содержание сухих веществ в жидкости СВ = 10%;

рабочая температура в реакторе ;

;

внутренний диаметр реактора D = 1м;

высота нижнего слоя жидкости ;

высота среднего слоя жидкости ;

высота верхнего слоя жидкости ;

объемная доля твердых частиц в нижнем слое Ф = 0,34;

плотностьтвердых частиц ³;

теплоемкость твердых частиц ;

теплопроводностьтвердых частиц ;

плотность жидкости в среднем слое = 992 кг/м³;

плотность жидкости в верхнем слое 868 кг/м³;

;

;

динамическая вязкость жидкости в верхнем слое Па*с;

теплопроводность жидкости в среднем слое ;

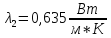теплопроводность жидкости в верхнем слое ;

частота вращения мешалки 1/с;

диаметр мешалки ;

коэффициент теплоотдачи от теплоносителя к наружной поверхности реактора Вт/м²*К;

теплопроводность материала стенки реактора 16 ;

толщина стенки реактора м;

теплоемкость сырья 3700;

расход сырья = 10^-3 кг/с;

интенсивность внутренних тепловыделений Вт/м³;

коэффициент теплопередачи от теплоносителя через рубашку к окружающей среде ²*К;

диаметр рубашки

средняя температура теплоносителя в рубашке ;

= 10;

начальная температура сырья на входе в реактор = 20;

начальная температура реактора с сырьем = 20 ;

коэффициент гидравлического сопротивления пузыря .

Расчеты выполняются в следующей последовательности.

1. Определяются молярная масса и плотность газовой смеси:

, (5.1.41)

где , – молярные массы газов.

где P – давление в реакторе ;

– универсальная газовая постоянная;

– абсолютная температура в реакторе.

2. По формулам (5.1.14), (5.1.15) определяются коэффициенты поверхностного натяжения и кинематической вязкости.

3. Плотность среды в нижнем слое – по (5.1.18)

4. Динамическая вязкость жидкости во втором слое:

5. Динамическая вязкость жидкости в первом слое – по (5.1.19)

6. Кинематические вязкости:

В нижнем слое

В среднем слое

В верхнем слое

7. Радиус отрыва пузырей – по формулам (5.1.1)

8. Газовыделение реактора:

где – общая высота слоя.

9. Частота выхода газовых пузырей из слоя:

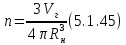
10. Скорость всплывания газового пузыря – по (5.1.8), (5.1.9).

Относительная скорость газового пузыря

11. Радиус пузыря, соответствующий максимальной скорости всплывания – по (5.1.10).

12. По формуле (5.1.23) определяется число Рейнольдса для нижнего слоя.

13. Число Прандтля определяется по формуле:

, (5.1.46)

Где теплоемкость и теплопроводность среды определяются по формулам (5.1.20) и (5.1.21).

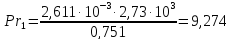
14. Число Нуссельта и коэффициент теплоотдачи для нижнего слоя – по (5.1.24), (5.1.25).

15. По формуле (5.1.23) определяется число Рейнольдса для среднего слоя.

16. Число Прандтля определяется по формуле (5.1.46)

17. Число Нуссельта и коэффициент теплоотдачи для среднего слоя – по формулам (5.1.26) и (5.1.25)

18. По формуле (5.1.23) определяется число Рейнольдса для верхнего слоя.

19. Число Прандтля определяется по формуле (5.1.46)

20. Число Нуссельта и коэффициент теплоотдачи для верхнего слоя – по формулам (5.1.26) и (5.1.25)

21. Средний коэффициент теплоотдачи – по формуле (5.1.27).

22. Зависимость рассчитывается по формуле (5.1.40). Для этого необходимо посчитать значения , по формулам (5.1.33) и (5.1.34), а так же найти значение .

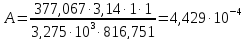
Где значения коэффициента теплопередачи от теплоносителя к реакционной смеси , общей массы реакционной смеси определяются по формулам (5.1.29) и (5.1.31).

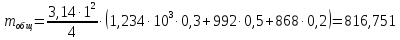
Средняя теплоемкость реакционной смеси определяется по формуле:

Значение найдем по формуле (5.1.38). Для этого предварительно найдем значения и по формулам (5.1.35) и (5.1.36)

Где общий объем реакционной смеси найдем по формуле (5.1.30):

Рис. 5.1. Зависимость радиуса газового пузыря от координаты z

Рис. 5.2. Зависимость температуры реакционной смеси от времени

Газовый пузырь быстро, за время достигает радиуса и дальше всплывает с постоянной скоростью (рис. 5.1).

Необходимо поддерживать мягкий режим нагревания или охлаждения реакционной смеси, поскольку резкие процессы нагревания-охлаждения неблагоприятно сказываются на жизнеспособности бактерий.

На рисунок 5.3, 5.4 показано влияние числа оборотов и температура теплоносителя на характер зависимости температуры среды от времени.

Уменьшение частоты вращения мешалки в 2 раза (до 0,1 1/с) приводит к увеличению времени нагревания реакционной смеси до 40°С с 4400 до 5100 с. (Рисунок). Увеличение температур теплоносителя с 40 до 60°С уменьшает необходимое время нагревания реакционной смеси до 1200 с (Рисунок).

Рисунок- Зависимость температуры реакционной смеси от времени при n=1 1/с

Рисунок- Зависимость температуры реакционной смеси от времени при n_м=1 1/с и t_тн=60 ⁰С

На рисунке показано влияние средней температуры теплоносителя на необходимое время разогрева реактора.

Рисунок - Зависимость времени нагревания реакционной смеси от температуры теплоносителя

Таким образом, разработанная программа позволяет смоделировать температурный режим реактора и разработать рекомендации по оптимальным величинам основных параметров процесса.