ЛЕКЦИЯ №1

ПРИНЦИПЫ ПРОГРАММНОГО УПРАВЛЕНИЯ

Прогресс человечества и его развития определяется интеллектуальными возможностями его индивидуума. Исторически сложилось так, что оценка интеллекта в значительной степени определяется изменением решать различные вычислительные задачи, иначе говоря, задачи математизированные. Естественно основным инструментом решения таких задач был мозг человека, однако, в процессе развития общества, решаемые задачи существенно усложнились и возможностей (ресурсов) мозга стало не хватать для эффективного и быстрого решения, поэтому из двух возможных путей преодоления проблемы (1) Развитие возможностей мозга. 2) Дополнение его возможностей с помощью внешних средств), на данном этапе развития, используется второй. При этом следует помнить, что эффективно работающие на решение задач устройства были созданы, по историческим меркам, практически вчера, т.е. не более 50 лет назад. В 1945 году в США фирмой IBM начались разработки эффективных вычислительных устройств, и к этой работе был привлечем математик Джон Фон Нейман, который впервые сформулировал ныне классические принципы программного управления к вычислительным устройствам (ППУ).

Любая математически сформулированная задача определяется в одно или несколько уравнений, при этом математически предлагают 2 варианта решения:

• аналитическое;

• численное.

Аналитическое решение есть упрощенная зависимость, определяющая связь искомой величины с исходными.

Численное решение есть вычисление рассматриваемой зависимости через подстановку конкретных значений исходных величин с выполнением над ними в указанных зависимостях операций.

ППУ опираются на 2 классических понятия в математике:

• данные;

• алгоритм.

Данные (операнд) – это величина, участвующая в вычислении в форме имени или значения, как правило – численного.

Алгоритм – это четкое последовательное и конечное предписание на выполнение действий над исходными данными для получения результата (операнда или выходного значения).

Вся сложность автоматизации вычислительного процесса заключалась в трудностях создания методики, обеспечивающей без участия человека, выполнения даже простейших действий над операндами, при этом подразумевалось, что сами устройства для выполнения таких действий создать возможно (типичный пример: механические счеты и арифмометры).

Сформулированные Нейманом принципы определили ключевой момент автоматизации вычислений, хранение в специальном устройстве вычислительной машины не только всех исходных операндов, но и алгоритма решения. При этом в качестве второго обязательного условия предлагалась запись алгоритма в виде, аналогичном записи данных, т.е. цифровом.

Алгоритм, как последовательность операций должен располагаться в памяти машины таким образом, чтобы обращение к каждому его компоненту можно было проводить достаточно просто, т.е. по адресу ячейки, в которой он хранится. ППУ позволяют сформировать простейшую закономерность:

Алгоритм – Операция

Программа – Команда

Схема показывает, что алгоритм есть совокупность элементарных действий, называемых операциями.

Операция – простейшее действие над операндом в процессе решения задачи. Типичные примеры: сложение, вычитание, умножение и деление.

При машинных вычислениях могут использоваться 2 дополнительные операции: чтение и запись, не имеющие односимвольных обозначений.

Применим ППУ к рассмотренным шести операциям, т.е. закодируем их обозначения в цифровом виде:

Помимо операций необходимо определить количество используемых в ней операндов:

• один;

• два;

• три.

Обозначив исходные операнды как PиZ, можно записать структуру простейших операций над ними, если в качестве обозначения операции используем символ,тогда одноадресная операция будет иметь структуру:P(Z) .

Для двухоперандной операции структура превращается в PZ.

Для трехоперандных простейших операций структура может быть представлена: T=P, где «=» определяет необходимость присваивания полученного справа от него значения к выходному операндуT, записанному слева.

Принципы Неймана предписывают представления операций и алгоритмов, в целом, в форме математизированного числового представления, при этом вводится 2 новых определения: команды и программы.

Команда – формализованное представление конкретной операции с указанием участвующих в ней операндов.

Программа – формализованная запись алгоритма решения на языке понятном вычислительной машине.

Важнейшим отличием команды от операции является то, что на ряду с собственно обозначениями операции, в ней указывается не сам операнд (операнды), а номера тех ячеек, в памяти которых он (они) хранятся. Тогда структура любой команды может быть представлена в виде:

КОП	Адресная часть

где КОП – код (цифровое обозначение операции), адресная часть – фрагмент команды с указанием адреса (адресов), участвующего в команде операндов.

С учетом рассмотренных ранее вариантов операций возможны 3 вида команд:

• одноадресные;

• двухадресные;

• трехадресные.

Структуры команд:

КОП

Адрес 1

КОП

Адрес 1

Адрес 2

КОП

Адрес 1

Адрес 2

Адрес 3

В соответствии с ППУ методика программирования любой математической задачи включая следующие разделы:

• формирование блока исходных данных и распределение их по ячейкам памяти;

• создание конкретного алгоритма решения и детализация его по до последовательности элементарных операций;

• вывод желаемого варианта используемых команд;

• создание последовательности команд, реализующих будущую программу;

• распределение команд программы в последовательность ячеек запоминающего устройства, желательно непрерывную (с точки зрения адресов этих ячеек).

Лекция №2

Рассмотренная методика упирается на заранее выполненный алгоритм решения задачи, при этом в общем виде решение любой задачи проходит следующие этапы предмашинной подготовки.

Представим схему решения задачи на ЭВМ в виде последовательности этапов:

Постановка задачи

Программирование задачи

Создание алгоритма решения

Выбор численного метода решения

Создание математической модели ее

Предмашинная подготовка

При работе команда ЭВМ в качестве исходной задачи будем использовать простейший математический вариант ее – конкретную формулу, не содержащую функций. Тогда можно сказать, что постановка задачи 1 вариант звучит следующим образом: вычислить значение переменной xпо заданной для нее математической зависимости.

x = (2a³b – 1200)/(0,8c + d).

Представленная в постановке задачи зависимость содержит только арифметические операции, т.е. является простейшей.

Анализ постановки задачи показывает, что имеющаяся в ней формула и является математической моделью задачи.

Выбор численного метода решения получения математической модели применяют лишь в случаях, содержания в модели неэлементарных действий (функциональная зависимость), например: тригонометрических функций, интегралов, дифференциалов и т.д. В нашем примере таких функций нет, поэтому в качестве метода решения выберем один из типовых, для элементарной математики:

1. линейный вычислительный процесс.

2. ветвящийся вычислительный процесс.

3. циклический вычислительный процесс.

Для рассматриваемого примера естественным является линейный вычислительный процесс. Создание алгоритма опирается на выбранный численный метод и созданную модель, причем по определению алгоритма, даже для нашего простейшего примера, могут быть десятки конкретных реализаций при максимальной детализации алгоритма – по операционной. В увеличенном варианте (минимальная детализация) алгоритм можно представить следующей графической схемой:

- [начало решения

- [ввод исходных данных

- [вычисление числителя

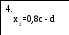
- [вычисление знаменателя

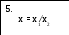
- [нахождение искомого результата

- [печать результата

- [окончание алгоритма

Алгоритм линейного вычислительного процесса составляется в виде блок-схемы, алгоритм является типовым для линейного вычислительного процесса и, как правило, для разных заданий будет отличаться лишь количеством вычислительных блоков и начинкой (содержанием блоков за исключением первого и последнего).

Создание графической схемы алгоритма позволяет считать выполненным четвертый из рассматриваемых этапов или третий с предмашинной подготовкой.

Создание алгоритма решения позволяет выполнить программирование задачи, как на машинном языке, так и любом алгоритмическом. В соответствии с целью лекции выполним программирование задачи в машинном варианте по предложенной в конце предыдущей лекции методике. В соответствии с этой методикой и требованием блока 2 алгоритма необходимо распределить исходные данные по ячейкам оперативной памяти ЭВМ, объемы оперативной памяти современной ЭВМ (адресные пространства их) находится в диапазоне сотен килобайт 100 Кбайт 100 Мбайт, поэтому истинные адреса составляющих их ячеек достаточно громоздки. Поэтому для учебных примеров выбираем простейшие, удобные для рассмотрения номера, например, трехадресная, начиная с ячейки с номером 100. Вся нумерация ячеек выполняется, как правило, в двойной системе исчисления или одной из промежуточных систем, вычисляемой как 2ⁿ, гдеn=1,2,3,4,5,6,7,8,9,10… и т.д.

Выберем для примера простейшую промежуточную систему n=3, т.е. восьмеричную, тогда первый из адресов будет обозначен 100₈. Выбрав номер первой из ячеек необходимо задаться стандартным объемом каждой из них. Объем каждой ячейки определяется в байтах или битах (1 байт = 8 бит), поэтому для работы с достаточно большими операндами исходных данных необходимо для каждого из них выделять не менее 4 байт (32 бита). Следовательно, номер следующей ячейки для размещения данных после 100₈будет 104₈, затем 110₈, 114₈, 120₈и т.д. Тогда рассмотрение примера распределения данных можно представить следующей таблицей.

Операнд	Адрес ячейки хранения
a b 1200 2	1008 1048 1108 1148
Операнд	Адрес ячейки хранения
0,8 c d	1208 1248 1308

Распределив исходные данные по ячейкам памяти ЭВМ выполним следующий этап методики, зададимся трехадресной структурой программ, выбирая на максимальную степень детализации, степень алгоритма.

Составим программу реализации алгоритма (начиная с блока 3) следующей схемой-таблицей:

КОП	Адрес 1	Адрес 2	Адрес 3	Пояснение
03 03 03 03 02 03 01 04	1008 1348 1348 1048 1348 1208 1408 1348	1008 1008 1148 1348 1108 1248 1308 1408	1348 1348 1348 1348 1348 1408 1408 1448	a2 134 ячейка a3 134 ячейка a3 2134 ячейка ba3 2134 ячейка x1 134 ячейка 0,8с 140 ячейка х2 140 ячейка х 144 ячейка

Реализовав требование блока 5, программа заканчивается, т.к. печать результата не может быть реализована одной элементарной командой, а требует использования специальных функций, рассмотрение которой на данном этапе не требует. Поэтому выполним последнее предписание методики: распределим составленные команды по ячейкам оперативной памяти, выбрав в качестве первого из адресов номер ячейки 500₈. Результат представим в таблице:

Команда	Адрес ячейки хранения
031001001348 031341001348 031341141348 031041341348 021341101348 031201241408 011401301408 041341401448	5008 5108 5208 5308 5408 5508 5608 5708

Распределив команды по ячейкам памяти, получаем наглядное подтверждение основного принципа Неймана по внешнему виду содержимое ячейки командой, есть целое число, т.е. операнд.

В виду большого количество размеров команды для размещения каждой используют восьмибайтовую ячейку.

Выводы: программирование в трехадресном варианте:

1. преимущества – достаточная компактность программ и логическая частота каждой из них, обеспечив полное представление для человека;

2. недостаток – серьезное усложнение каждой команды с указанием трех адресов, причем в некоторых случаях указания ячейки размещения результата избыточно;