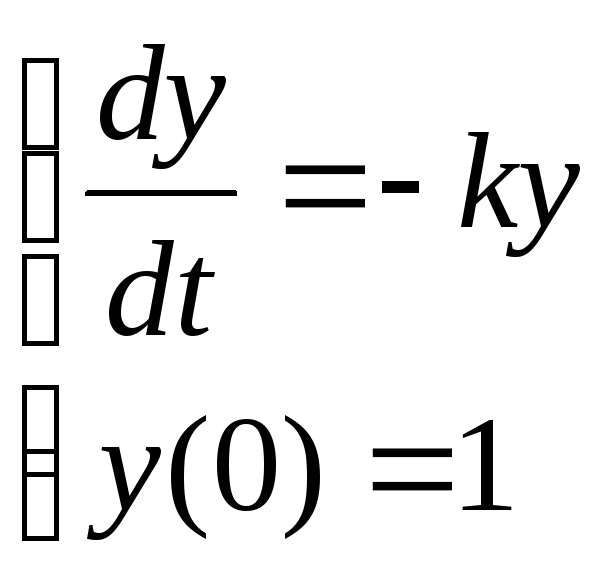Глава 1. Математическое и программное обеспечение процесса моделирования
Тема 1. Математическое введение
1.1. Линейная алгебра и математический анализ
1. Повторите основные понятия линейной алгебры: линейное пространство, векторы, линейная комбинация векторов, линейная зависимость векторов, матрицы, ранг матрицы, действия с матрицами, обратная и транспонированная матрица, вычисление определителя.
2. Повторите основные понятия математического анализа: пределы, методы вычисления производных и простейших интегралов (табличных); обыкновенные дифференциальные уравнения (ОДУ) с разделяющимися переменными, линейные ОДУ 1-го порядка, задача Коши.
3. Вспомните следующие понятия: прямая и обратная теоремы, необходимые и достаточные условия.
Пределы.
Def. Постоянное число а называется пределом последовательности {xn}, если для любого > 0, сколь бы мало оно ни было, существует номер N, что для любого n N выполняется неравенство | xn – a | < . Иными словами, весь «хвост» последовательности {xn} близок к числу a.
Тот
факт, что а
является пределом последовательности
{xn},
записывается так:
,
илиxn
а.
Особый интерес представляет случай, когда xn 0.
Def. Последовательность {xn}, имеющая пределом 0, называется бесконечно малой величиной (БМВ).
Пусть мы имеем дело с несколькими последовательностями, каждая из которых является БМВ. Представляет интерес сравнение двух различных БМВ по характеру («скорости») их приближения к 0.
Пусть имеем две БМВ: xn и уn.
Def.
I.
Если отношение
имеет конечный и отличный от 0 предел,
тоxn
и уn
считаются величинами
одного порядка.
Def.
II.
Если отношение
имеет 0 предел, равный 0, т.е. само
оказывается БМВ, тоxn
считается бесконечно малой более
высокого порядка,
чем уn.
Иными словами, {xn}
«быстрее» стремится к 0, чем {уn}.
Пример
1.1. Пусть xn
=
,уn
=
,zn
=
.
Тогда
,
.
Это значит, чтоxn
и уn
являются величинами одного порядка, а
zn
является бесконечно малой более высокого
порядка, чем xn.
Если БМВ xn является бесконечно малой более высокого порядка, чем уn, то этот факт записывается так: xn = о(уn).
Замечание. Поскольку характер стремления к 0 последовательности не зависит от её знака, то величина о(уn) считается как бы не имеющей знака. Иными словами если xn = о(уn), то также –xn = о(уn) и xn = о(– уn). Отсюда получаются «странные» формулы типа о(уn) = – о( уn).
Далее. Поскольку БМВ не перестаёт быть таковой при умножении её на ненулевую константу, то справедливы, например такие формулы о(уn) = о( уn) + о(уn) или о(уn) = 5о( уn) и т.д.
Задачи
Дано:
.
Вычислитьdet
(A)
разложением по 1-й строке.
Дано:
.
Вычислитьdet
(A)
разложением по 3-му столбцу.
Дайте определение понятия «линейная комбинация векторов». Образуйте любую линейную комбинацию из векторов
;
;
.
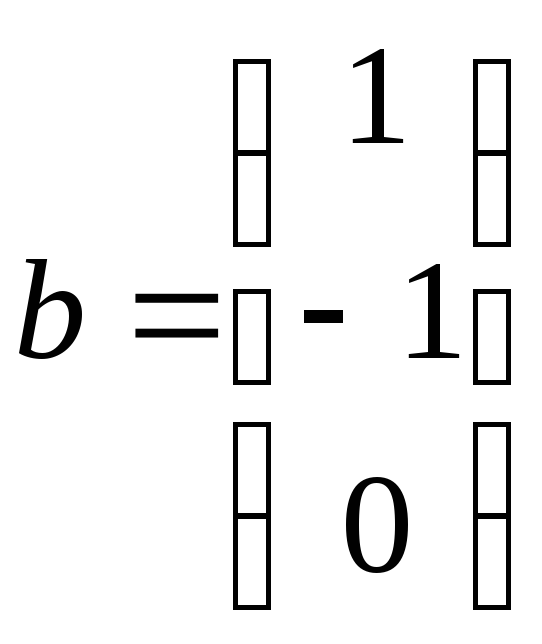Какие векторы называются линейно зависимыми, а какие – линейно независимыми? Являются ли линейно зависимыми следующие три вектора
;
;
.
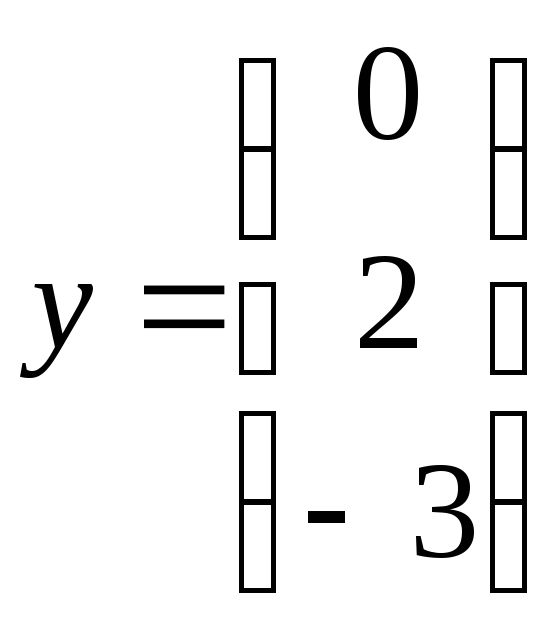Что такое «ранг матрицы»? Чему равны ранги следующих матриц
?
Ответ объяснить.Какая из следующих матриц является обратной к матрице C =
:
Дано:
;
.
ВычислитьB
АT
A.В следующем предложении вместо многоточия поставьте: «необходимо», «достаточно» или «необходимо и достаточно». Для того чтобы сумма двух целых чисел была чётной,….., чтобы каждое слагаемое было чётным.
В следующем предложении вместо многоточия поставьте: «необходимо», «достаточно» или «необходимо и достаточно». Для того чтобы число делилось на 15,……., чтобы оно делилось на 5.
В следующем предложении вместо многоточия поставьте: «необходимо», «достаточно» или «необходимо и достаточно». Для того чтобы число делилось на 10,….., чтобы оно делилось на 2 и 5.
Среди заданных БМВ определить, какие из них имеют одинаковый порядок с xn =
,
а какие равныо(xn):
а)
б)
в) 2– n
г) e
– 2 n
д)
.
12.
Вычислить производную
.
13.
Вычислить определённый интеграл
.
14.
Решить задачу Коши
