- •Министерство образования и науки российской федерации
- •Введение
- •Методические указания, примеры выполнения заданий задание 1
- •Решение системы методом определителей.
- •Решение систем матричным методом.
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задание 10
- •Задание 11
- •Учебное Пособие для выполнения контрольной работы № 1 по математике
- •394036 Воронеж, пр. Революции, 19.
Задание 6
В данном задании требуется вычислить пределы, не пользуясь правилом Лопиталя. Для этого рассмотрим некоторые теоретические сведения.
Если
функция
![]() в окрестности точки
в окрестности точки![]() определена и непрерывна, то ее предел
можно вычислить по формуле:
определена и непрерывна, то ее предел
можно вычислить по формуле:
![]()
Поэтому
при вычислении пределов надо вначале
убедиться, является ли функция
![]() непрерывной, или она разрывная в
окрестности точки
непрерывной, или она разрывная в
окрестности точки![]() путем прямой подстановки
путем прямой подстановки![]() в выражение функции
в выражение функции![]() .
Если
.
Если![]() не существует при
не существует при![]() ,
то тогда следует находить предел
,
то тогда следует находить предел![]() .
Для этого применяют специальные приемы.
.
Для этого применяют специальные приемы.
Разрывные
функции часто имеют неопределенные
значения в точке разрыва
![]() .
Неопределенности бывают следующих
типов 1)
.
Неопределенности бывают следующих
типов 1)![]() 2)
2)![]() 3)
3)![]() 4)
4)![]() 5)
5)![]() .
Это – символическое обозначение
неопределенностей. Если функция имеет
вид дроби
.
Это – символическое обозначение
неопределенностей. Если функция имеет
вид дроби![]() ,
у которой при
,
у которой при![]() числитель и знаменатель одновременно
обращаются в ноль, т. е.
числитель и знаменатель одновременно
обращаются в ноль, т. е.![]() и
и![]() ,
то такая неопределенность обозначается
,
то такая неопределенность обозначается![]() .
Если же при
.
Если же при![]() имеем
имеем![]() и
и![]() одновременно, то неопределенность
обозначается
одновременно, то неопределенность
обозначается![]() .
Функция может иметь вид произведения
.
Функция может иметь вид произведения![]() .
Если при этом
.
Если при этом![]() и при
и при![]()
![]() ,
то такую неопределенность обозначают
,
то такую неопределенность обозначают![]() .
Возможен случай, когда функция имеет
вид разности
.
Возможен случай, когда функция имеет
вид разности![]() ,
причем при
,
причем при![]()
![]() и
и![]() одновременно. Здесь возникает
неопределенность типа
одновременно. Здесь возникает
неопределенность типа![]() .
Еще может быть вариант, когда функция
имеет вид
.
Еще может быть вариант, когда функция
имеет вид![]() и
и![]() ,
а при
,
а при![]()
![]() .
Такая неопределенность обозначается
.
Такая неопределенность обозначается![]() .
Для раскрытия подобных неопределенностей
применяются специальные преобразования,
которые допустимы правилами математики.
После этого получаем выражения без
неопределенностей и можно будет вычислить
предел.
.
Для раскрытия подобных неопределенностей
применяются специальные преобразования,
которые допустимы правилами математики.
После этого получаем выражения без
неопределенностей и можно будет вычислить
предел.
Для
случая, когда
![]() имеет вид рациональной дроби и
имеет вид рациональной дроби и![]() ,
имеем неопределенность типа
,
имеем неопределенность типа![]() ,
для вычисления которой надо числитель
и знаменатель дроби поделить на старшую
степень знаменателя.
,
для вычисления которой надо числитель
и знаменатель дроби поделить на старшую
степень знаменателя.
Пример
для задания а):
![]() .
Имеем неопределенность вида
.
Имеем неопределенность вида![]() .
Чтобы раскрыть эту неопределенность
разделим числитель и знаменатель на
.
Чтобы раскрыть эту неопределенность
разделим числитель и знаменатель на![]() .Получим
.Получим![]() .
Так как при
.
Так как при![]()
![]()
![]() ,
то имеем
,
то имеем![]() .
.
Во
втором примере функция имеет вид дроби
![]() ,
у которой числителем и знаменателем
являются рациональные выражения, которые
содержат только целые положительные
степени переменной
,
у которой числителем и знаменателем
являются рациональные выражения, которые
содержат только целые положительные
степени переменной![]() .
Если при
.
Если при![]() числитель
числитель![]() и знаменатель
и знаменатель![]() ,
то
,
то![]() и
и![]() нацело (без остатка) делятся на разность
(
нацело (без остатка) делятся на разность
(![]() ).
Это деление осуществляется углом.
).
Это деление осуществляется углом.
Пример
для задания б):
![]() .
Так при
.
Так при![]() имеем
имеем![]() и
и![]() ,
то
,
то
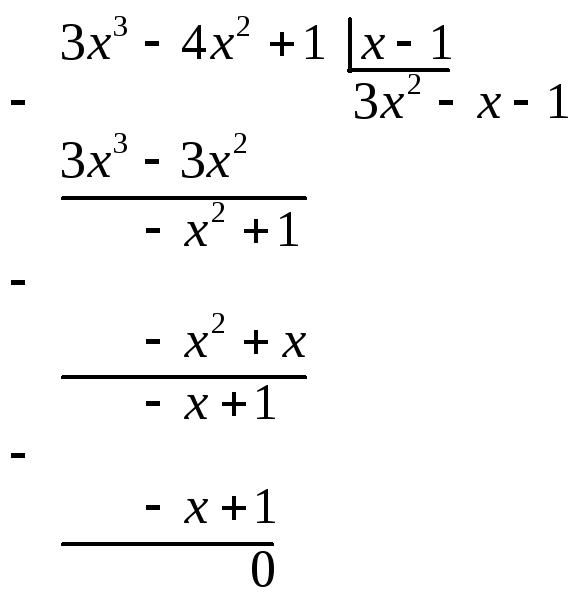
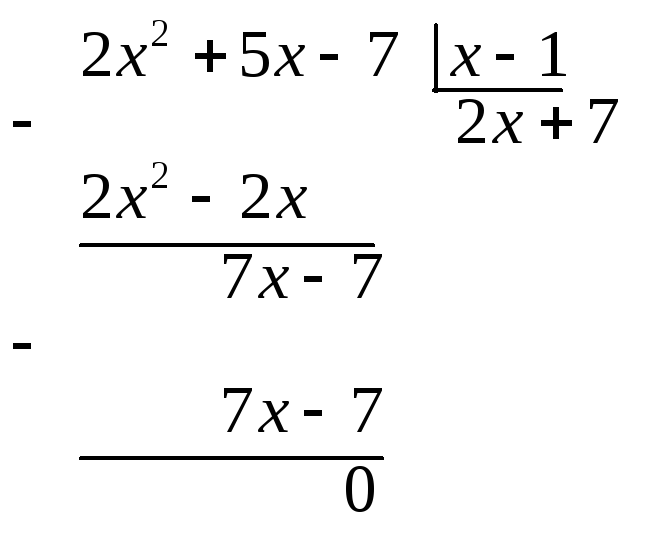 .
.
Теперь числитель и знаменатель первоначальной дроби можно представить произведением, что помогает вычислить предел
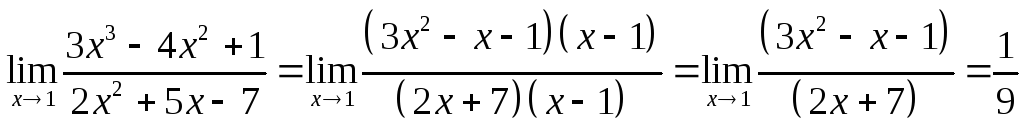 .
.
В
третьем примере (в) вычисляется предел
при
![]() для неопределенности типа
для неопределенности типа![]() с участием тригонометрических функций.
Для выполнения этого задания следует
использовать первый замечательный
предел или его разновидности
с участием тригонометрических функций.
Для выполнения этого задания следует
использовать первый замечательный
предел или его разновидности
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
Кроме того нужны некоторые формулы из тригонометрии
![]() ,
,
![]() ,
,![]() .
.
Пример для задания в):
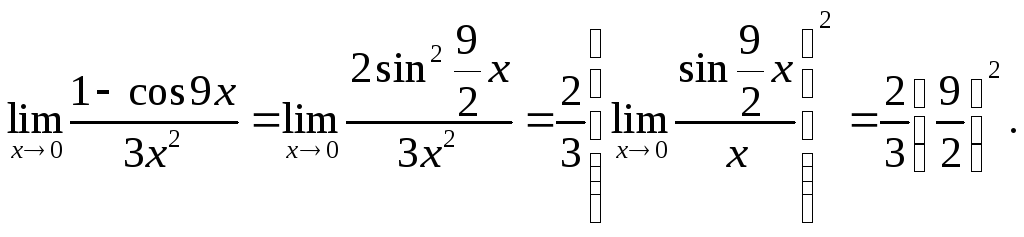
В
заданиях (г) требуется раскрыть
неопределенность типа
![]() ,
либо
,
либо![]() .
Для их вычисления следует использовать
второй замечательный предел
.
Для их вычисления следует использовать
второй замечательный предел
![]() ;
;
![]()
и свойства логарифмов
![]() ;
;
![]() .
.
Примеры для задания г):
1)
![]()
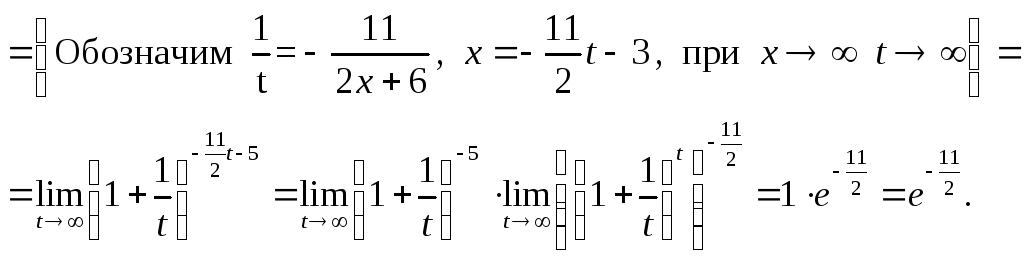
2)
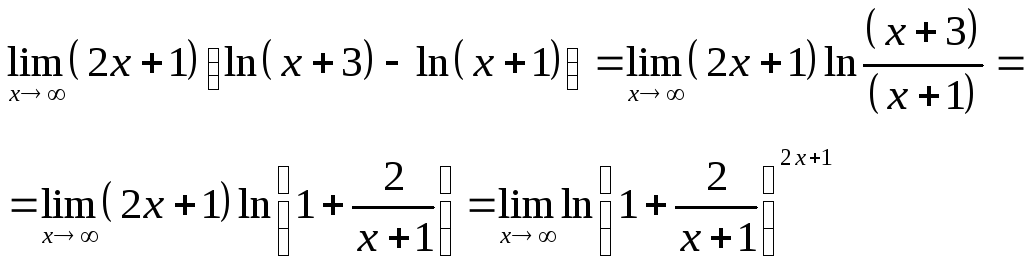
Так
как функция
![]() непрерывная, то можно перейти к пределу
под знаком функции, т.е.
непрерывная, то можно перейти к пределу
под знаком функции, т.е.

ЗАДАНИЕ 7
Для нахождения производных необходимо знание основных формул дифференцирования.
Правила дифференцирования
Пусть
![]() ,
,![]() ,
,![]() ,
тогда
,
тогда
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Производная
сложной функции
![]() .
.
Таблица производных
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
формула для логарифмического дифференцирования
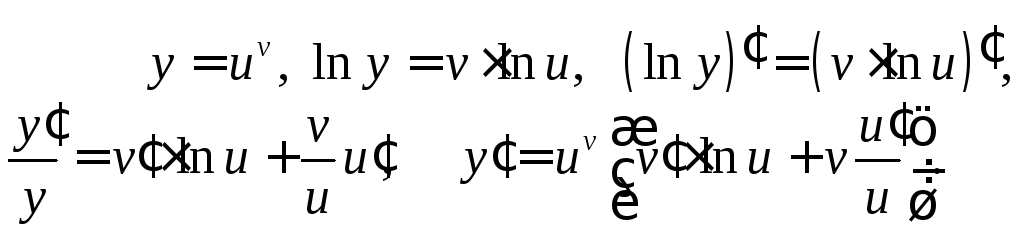 (27)
(27)
Примеры для заданий а) и б):
![]() .
Находим производную от произведения
функций.
.
Находим производную от произведения
функций.
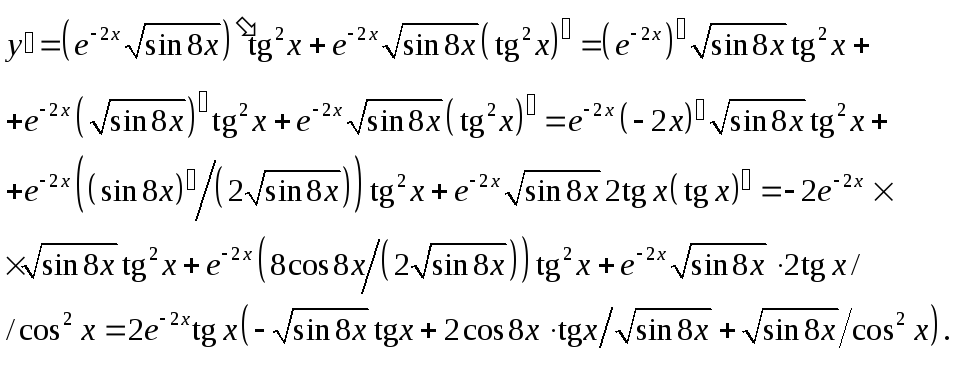
![]() .
.

![]() .
.
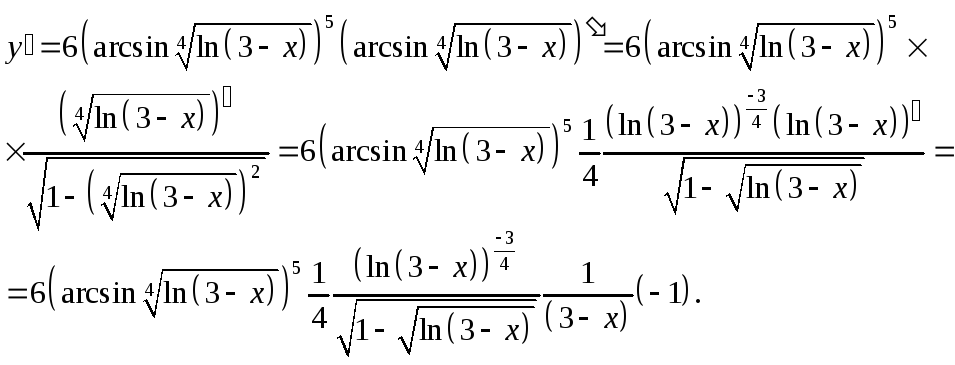
Пример для задания в):
![]() .
Используя формулу (27), найдем
.
Используя формулу (27), найдем
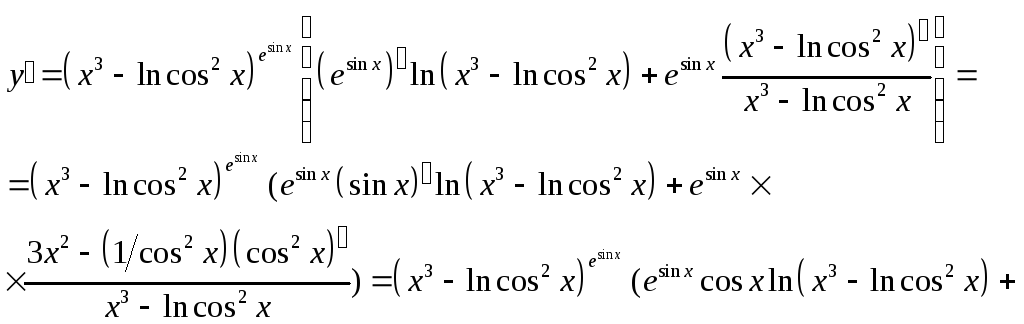
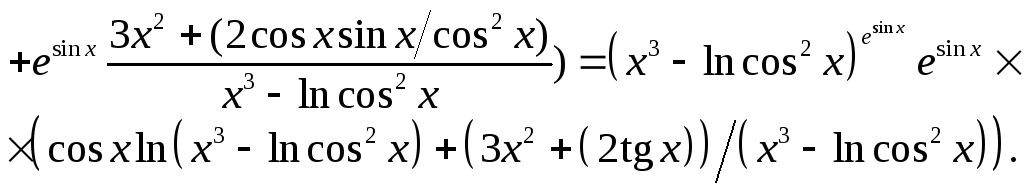
Пример
для задания г):
![]() .
Переменная
.
Переменная![]() задана как неявная функция. Продифференцируем
обе части равенства, считая
задана как неявная функция. Продифференцируем
обе части равенства, считая![]() функцией от
функцией от![]() .
.
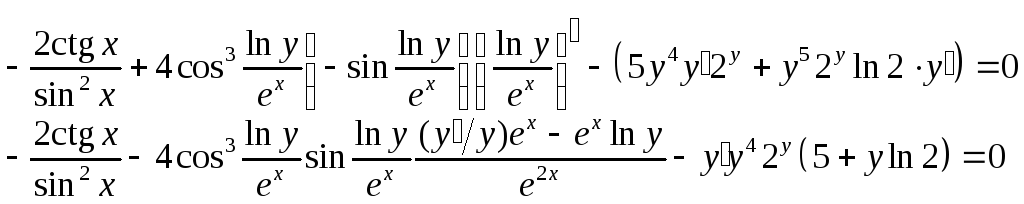
Объединив
члены, содержащие
![]()
![]()
найдем
![]()
ЗАДАНИЕ 8
Найти первую и вторую производные функции.
Пример.
а):
![]() .
Найдем первую производную
.
Найдем первую производную![]() :
:
![]()
![]() Дифференцируя
выражение для
Дифференцируя
выражение для
![]() ,вычислим вторую
производную
,вычислим вторую
производную
![]() :
:![]()
![]()
б)
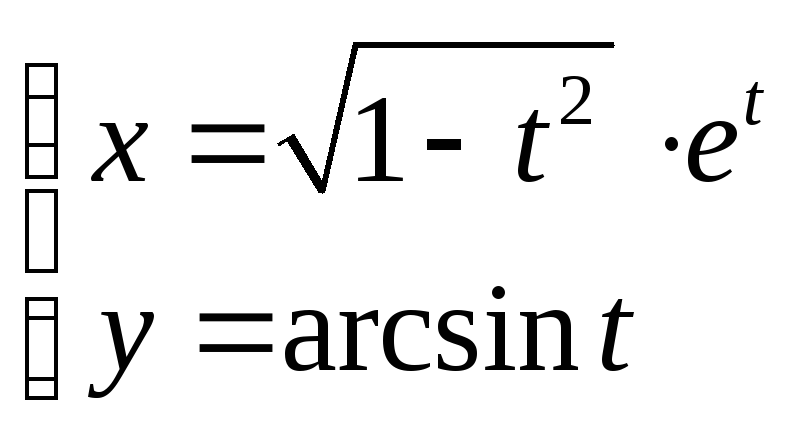 .
.
Функция задана параметрически. Вычислим
![]() ,
,
![]() .
Первая производная
.
Первая производная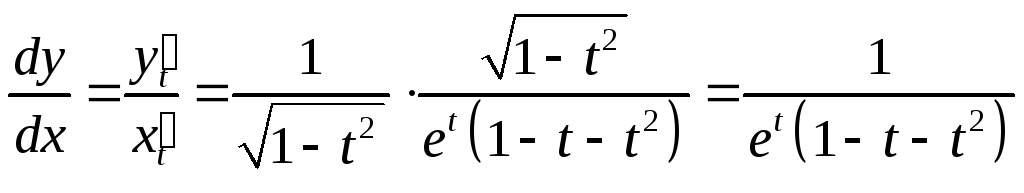 .
.
Вторая
производная
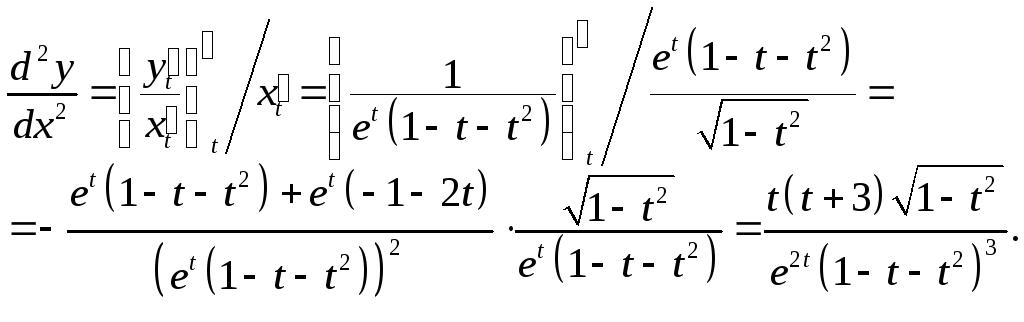
Этот
же результат можно получить, если
воспользоваться для нахождения второй
производной формулой
![]() ,
вычислив
,
вычислив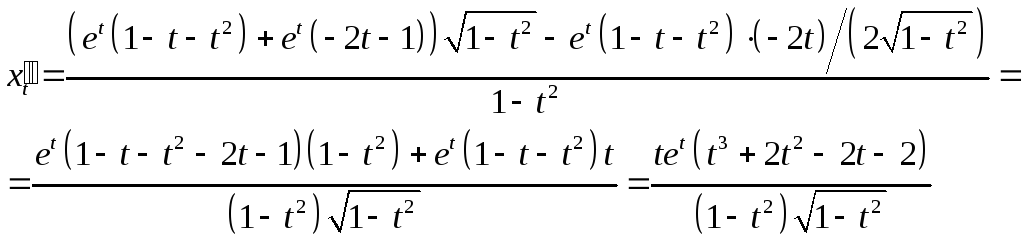 и
и![]() .
.
Задание 9
Исследовать функцию и построить ее график.
Пример.
Рассмотрим функцию
![]() .
.
1.
Данная функция существует при всех
значениях кроме точек, где знаменатель
обращается в ноль
![]() .
Поэтому областью определения функции
являются все действительные числа,
кроме чисел
.
Поэтому областью определения функции
являются все действительные числа,
кроме чисел![]() ,
а именно:
,
а именно:
![]() .
.
2.
Данная функция
![]() является нечетной, так как
является нечетной, так как![]() .
Функция непериодическая.
.
Функция непериодическая.
3. Найдем интервалы возрастания и убывания функции, точки экстремума. Для этого вычислим первую производную
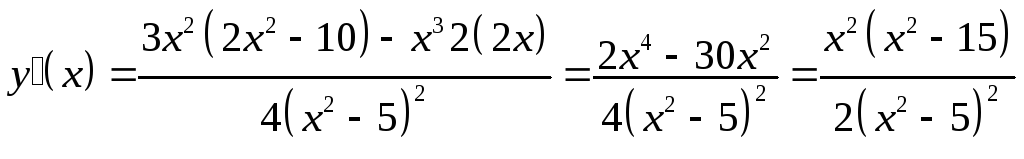 .
(28)
.
(28)
Используем
необходимый признак экстремума: если
функция имеет экстремум в некоторой
точке, то первая производная в этой
точке либо равна нулю, либо не существует.
Из (28) найдем, что первая производная
равна нулю при
![]() и
и![]() ;
не существует при
;
не существует при![]() ,
но последние два значения не входят в
область определения функции. Точки
,
но последние два значения не входят в
область определения функции. Точки![]() и
и![]() разбивают область определения функции
на интервалы
разбивают область определения функции
на интервалы
![]() .
.
Чтобы определить, возрастает или убывает функция на каждом из перечисленных интервалов, воспользуемся достаточным признаком возрастания (убывания) функции.
Найдем
знак первой производной в каждом из
интервалов. Для этого возьмем любое
значение переменой
![]() из соответственного интервала и,
подставим его в выражение для
из соответственного интервала и,
подставим его в выражение для![]() и определим знак первой производной
при выбранном значении
и определим знак первой производной
при выбранном значении![]() .
Так, в интервале
.
Так, в интервале![]()
![]() ,
значит, функция на этом интервале
возрастает. В интервале
,
значит, функция на этом интервале
возрастает. В интервале![]()
![]() ,
т. е. функция на этом интервале убывает
и т. д.
,
т. е. функция на этом интервале убывает
и т. д.
Результаты
исследования записаны в таблице 1. Здесь
же даны выводы о том, является ли
критическая точка экстремальной или
нет при помощи достаточного признака
экстремума функции в критической точке
по
![]() .
Из таблицы 1 видно, что при
.
Из таблицы 1 видно, что при![]() функция достигает максимума (
функция достигает максимума (![]() ).
Точка
).
Точка![]() является точкой минимума (
является точкой минимума (![]() ),так как при
переходе через эту критическую точку
производная
),так как при
переходе через эту критическую точку
производная
![]() меняет знак с « – » на « +».
меняет знак с « – » на « +».
Таблица 1
|
|
|
|
|
|
|
0 |
|
|
+ |
0 |
- |
Не сущ. |
- |
0 |
|
|
|
max |
|
Не сущ. |
|
0 |
Продолжение таблицы 1
-
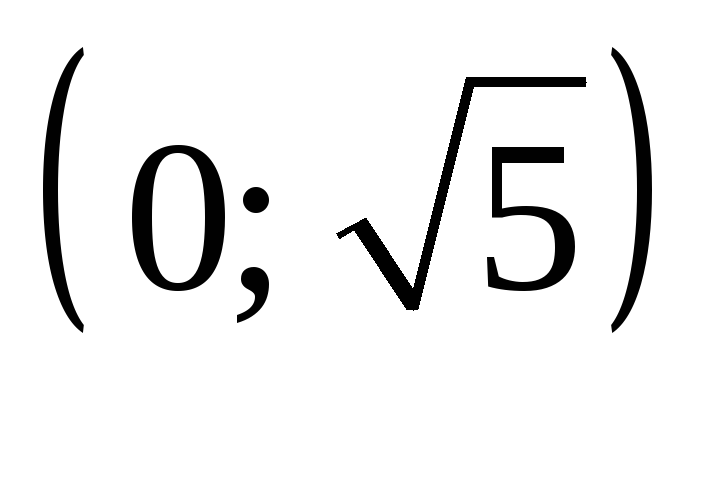

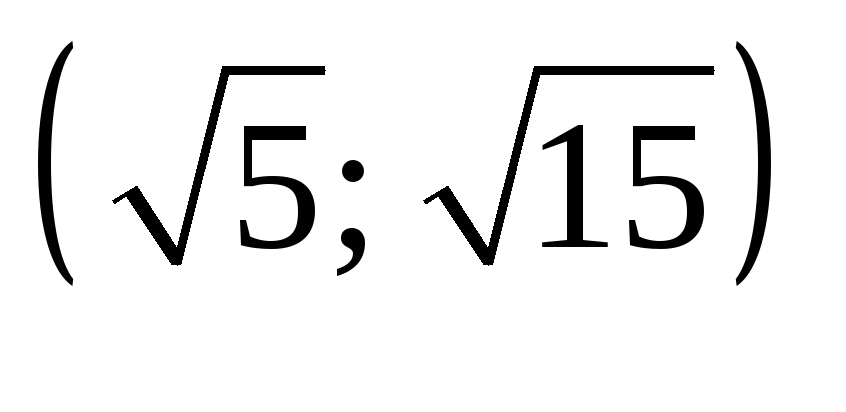
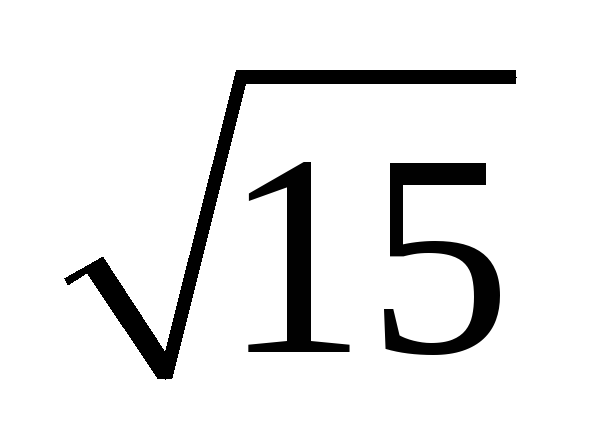
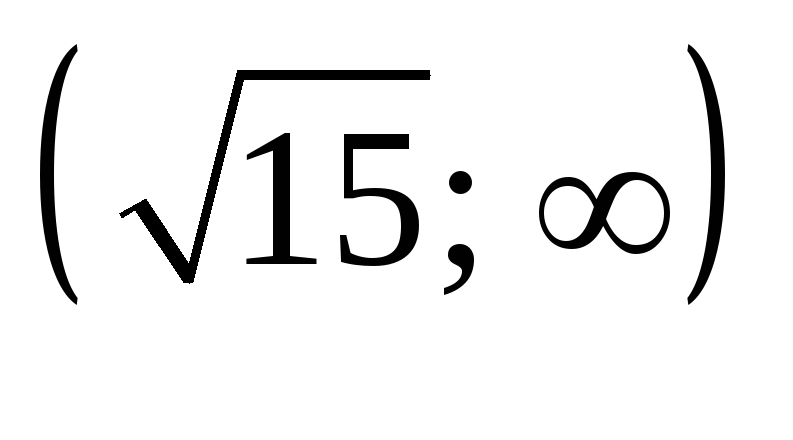
-
Не сущ.
-
0
+
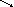
Не сущ.
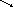
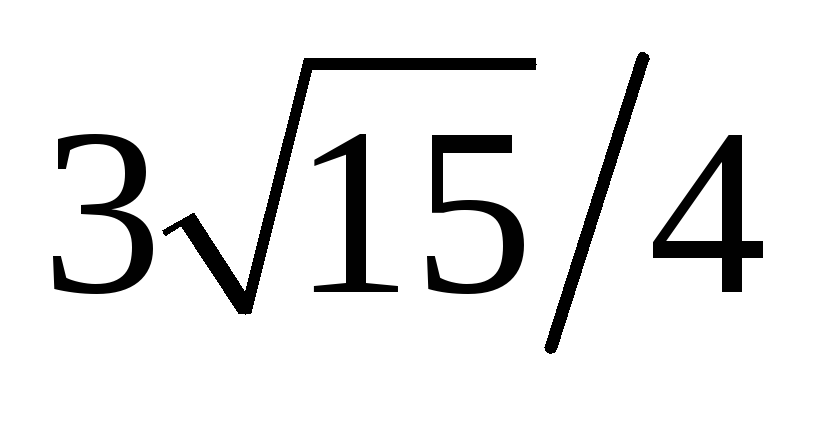 min
min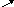
4.
Вычисляя
![]() ,
найдем интервалы выпуклости, вогнутости
и точки перегиба (таблица 2).
,
найдем интервалы выпуклости, вогнутости
и точки перегиба (таблица 2).
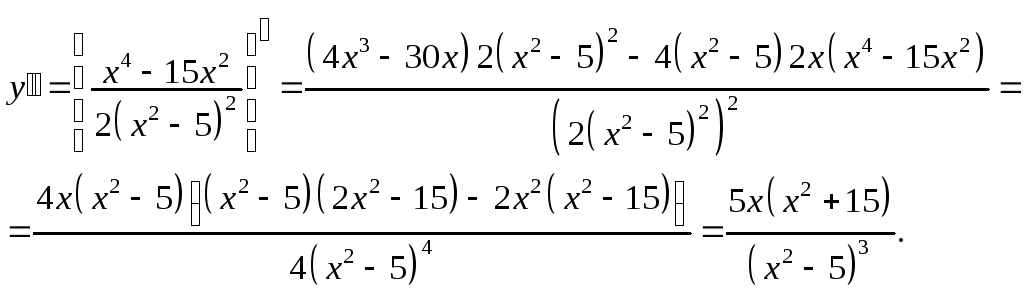
Отсюда
имеем
![]() при
при
![]() ,
а при
,
а при![]()
![]() не существует. Так как при
не существует. Так как при![]() и функция не существует, то стационарной
точкой для второй производной является
только
и функция не существует, то стационарной
точкой для второй производной является
только![]() .
Эта точка разбивает область определения
функции на промежутки
.
Эта точка разбивает область определения
функции на промежутки
![]() .
.
Таблица 2
|
|
|
|
|
0 |
|
|
|
|
|
- |
Не сущ. |
+ |
0 |
- |
Не сущ. |
+ |
|
|
|
Не сущ. |
|
0 |
|
Не сущ. |
|
Отсюда видно, что начало координат О (0; 0) – точка перегиба графика.
5. Найдем асимптоты графика функции:
а) Вертикальные асимптоты.
Так
как в данном случае функция имеет вид
дроби, то из условия обращения в ноль
знаменателя найдем вертикальные
асимптоты:![]() .
Так как
.
Так как
![]() ,
то по определению прямые
,
то по определению прямые
![]() и
и![]() являются вертикальными асимптотами.
являются вертикальными асимптотами.
б)
Наклонные асимптоты (![]() ).
).
![]() ;
;
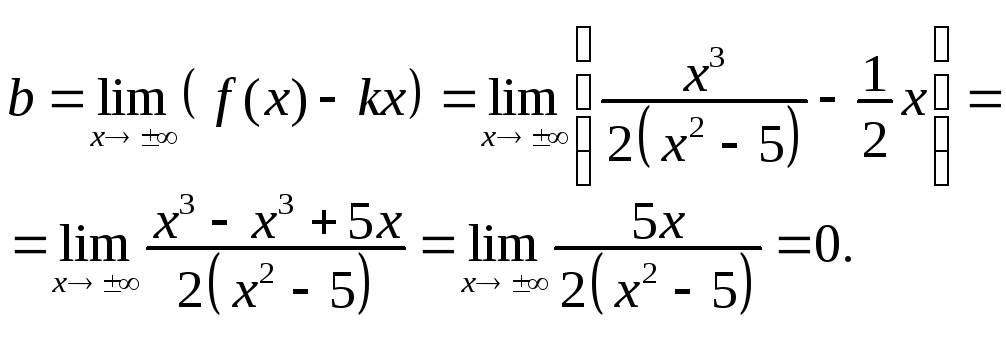
![]() –наклонная
асимптота графика функции.
–наклонная
асимптота графика функции.
6.
Точкой пересечения графика функции с
осями координат будет точка О(0;0), так
как при
![]() имеем
имеем![]() .
.
Таким
образом, функция возрастает на интервалах
![]() и
и![]() ,
убывает на интервалах
,
убывает на интервалах![]() ,
,![]() ,
,![]() ,
,![]() является выпуклой при
является выпуклой при![]() ,
,![]() и вогнута при
и вогнута при![]() и
и![]() .
.
Строим
график функции (рисунок 1), отметив
вначале на плоскости
![]() асимптоты графика функции
асимптоты графика функции![]() ,
,![]() ;
точки экстремума функции
;
точки экстремума функции![]() (
(![]() )
и
)
и![]() (
(![]() ),
точку перегиба О(0;0).
),
точку перегиба О(0;0).
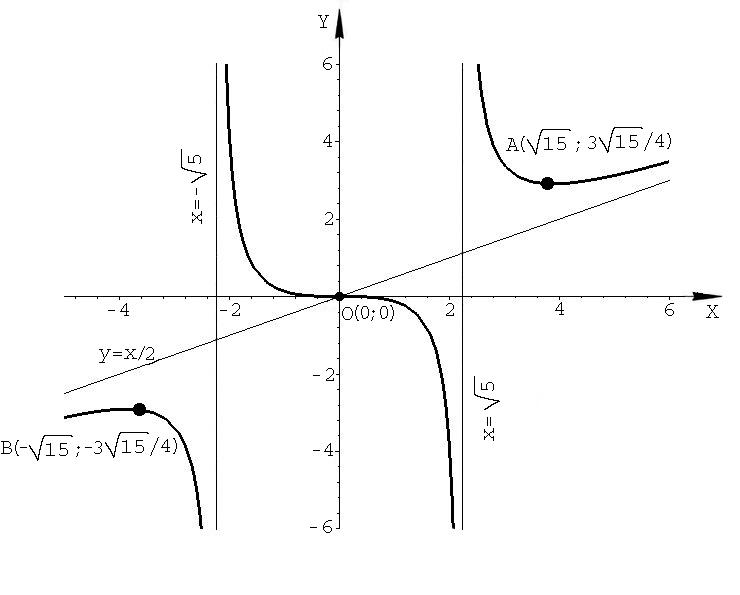
Рис. 1 Чертеж к заданию 4.