Задание 4

Окружностью называется геометрическое место точек плоскости, равноудаленных от данной точки, называемой центром. Расстояние от точек окружности до центра называется радиусом.

Уравнением окружности радиуса R с центром в начале координат является выражение

.

Если центр окружности находится не в начале координат, а в произвольной точке , то ее уравнение имеет вид

. (21)

Раскрывая скобки в (21) получим

. (22)

Чтобы от уравнения (22) перейти к (21) нужно применить метод выделения полного квадрата. Рассмотрим алгоритм этих преобразований.

Дана окружность .

.

.

.

,

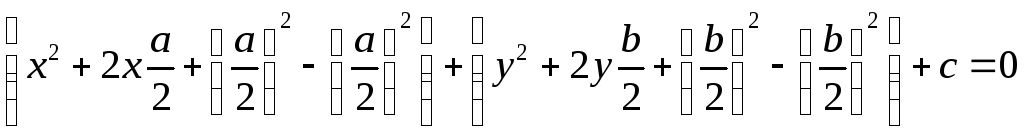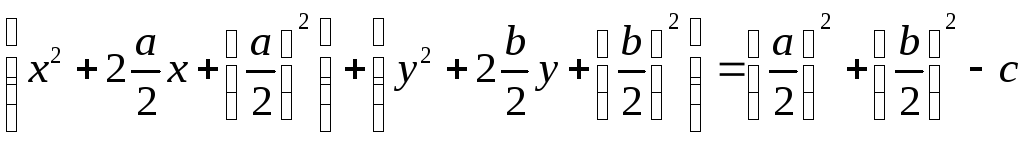где .

Получили уравнение окружности с центром в т. и радиусомR в системе координат .

Обозначая , абудем иметь уравнение окружности в новой системе координат

.

Центр ее находится в т. , радиус равенR.

Пример. Дано уравнение окружности . Методом выделения полного квадрата привести его к виду. Путем параллельного переноса системы координат привести последнее уравнение к виду. Построить обе системы координат, найти в каждой из них центр окружности. Сделать чертеж.

Решение. .

.

.

.

Центр окружности находится в т. , радиус равен 10. Введем новые переменныеи, тогда в новой системе координатокружность примет вид. Центр ее совпадает с началом координат.

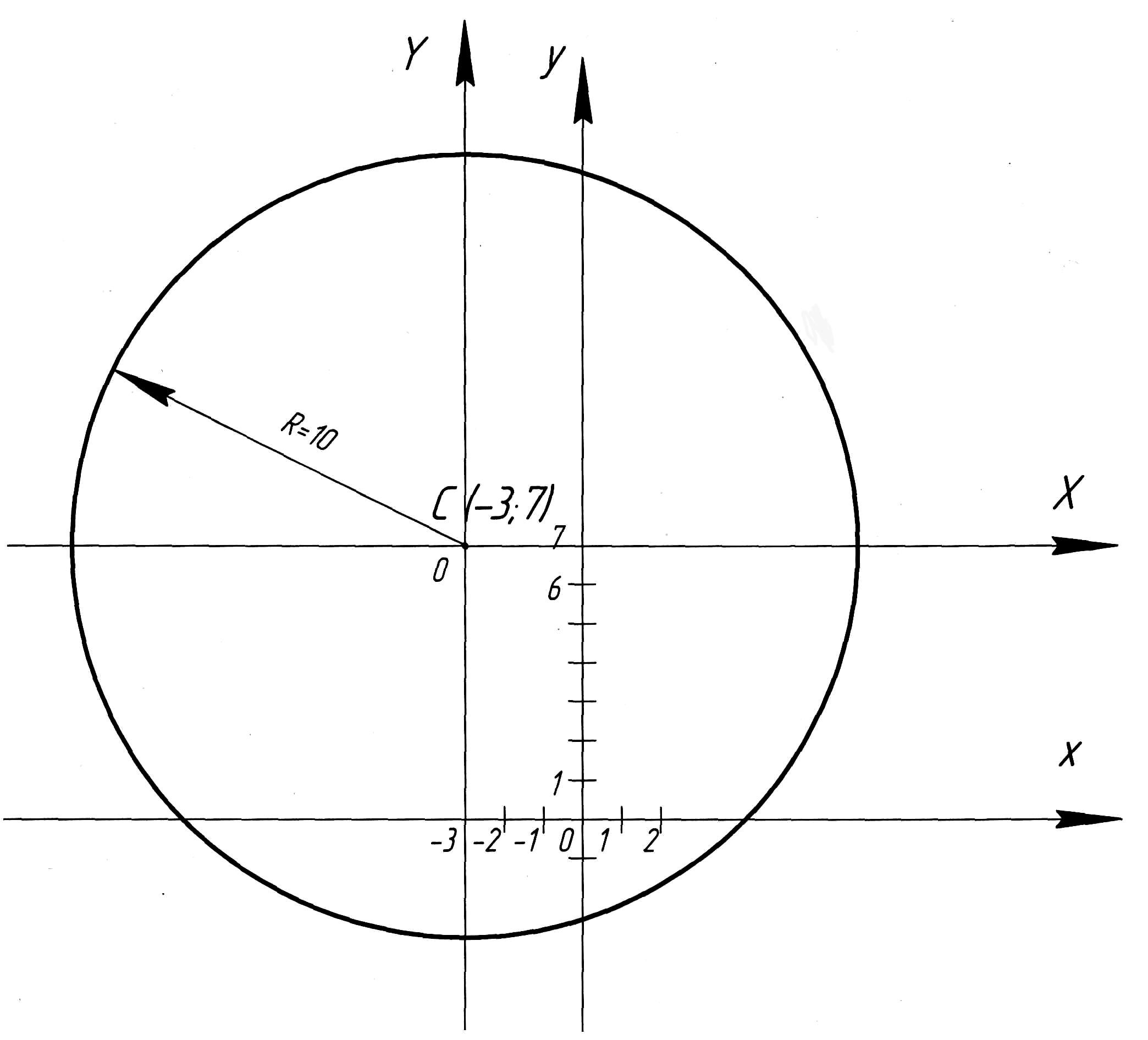
Рис. 2. Чертеж к заданию 4.

Задание 5

В этом задании рассматриваются вопросы аналитической геометрии в пространстве.

1) Уравнение плоскости, проходящей через три данные точки ;;находятся по формуле

.

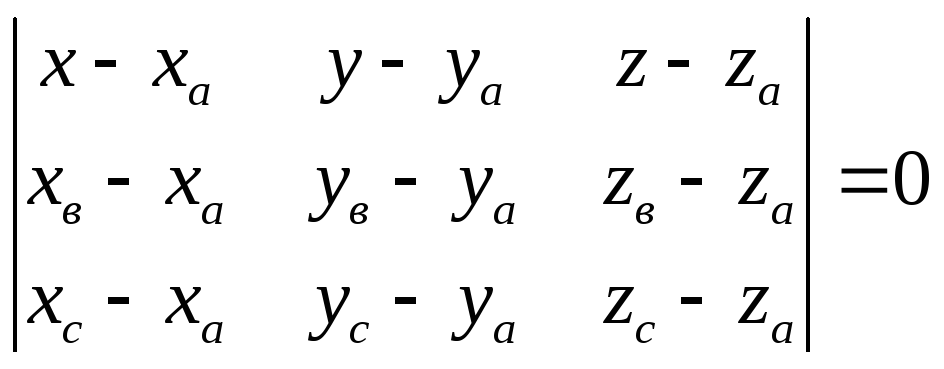Ответ нужно представить в общем виде уравнения плоскости

.

2) Для отыскания угла между прямой и плоскостью нужно:

а) написать уравнение прямой, проходящей через две данные точки: и, по формуле:

. (23)

Направляющий вектор этой прямой имеет координаты

.

б) угол между прямой и плоскостью в пространстве находится по формуле:

;

,

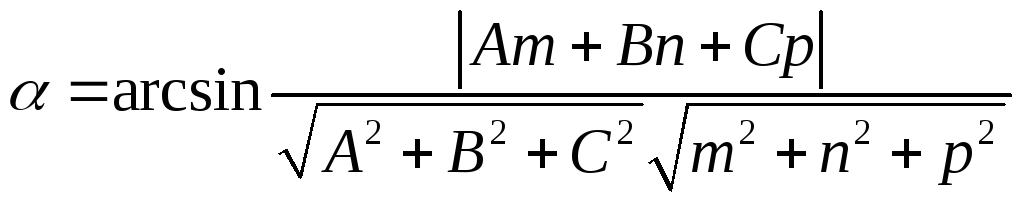где - координаты нормального вектораберутся из общего уравнения плоскости, как коэффициенты передисоответствено.

3) Уравнение прямой, проходящей через две точки, было приведено ранее (23).

4) Для того, чтобы найти уравнения высоты пирамиды, опущенной из точки на грань, удобно воспользоваться каноническими уравнениями прямой в пространстве

,

где – координаты точки, лежащей на прямой. В данном случае нам известны координаты точки. Проекции направляющего векторанайдем из условия перпендикулярности прямой и плоскости. Так как вектор нормалик плоскости и направляющий векторпрямой параллельны, то в качестве направляющего вектора можно взять вектор, т.е..

5) Основанием высоты является точка пересечения прямой, проходящей через высоту, с плоскостью основания . Для нахождения этой точки пересечения решим систему уравнений:

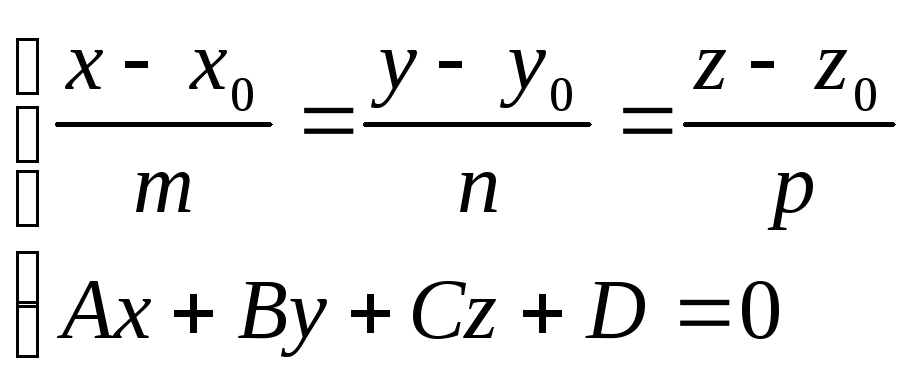
Эту систему удобно решать, если перейти к уравнению прямой в параметрическом виде

(*)

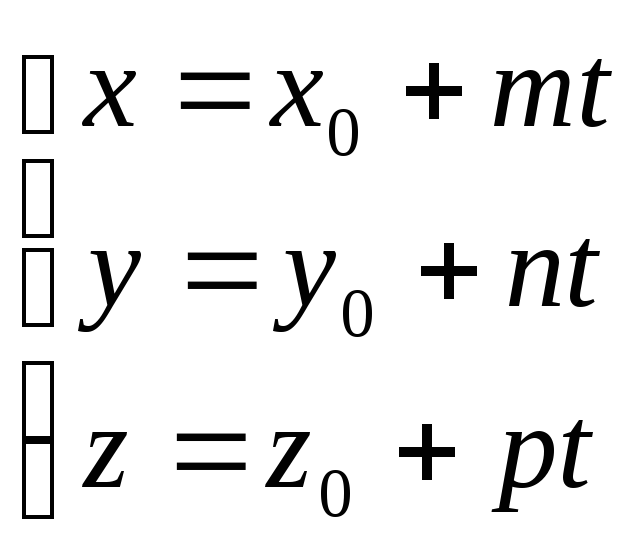Подставим выраженные переменные черезиз (*) в уравнение плоскости

.

Отсюда найдем параметр t, подставим его в уравнение прямой и получим координаты искомой точки пересечения прямой с плоскостью.

Пример. В пирамиде из задания 2 найти: 1) уравнение плоскости АВС;2) угол между ребромADи граньюАВС;3) уравнение прямой АВ;4) уравнение высоты, опущенной из вершины D на грань АВС; 5) основание этой высоты.

Решение.

1) уравнение плоскости выразим через определитель

.

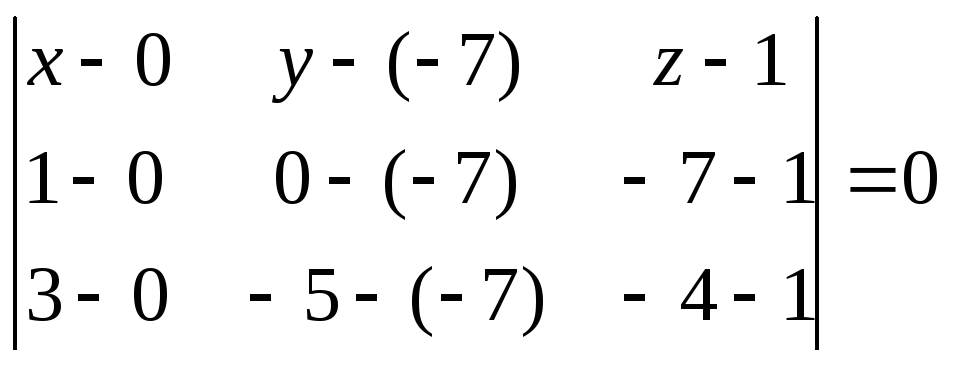Решив его, получим уравнение грани (АВС) . Отсюда находим вектор нормали. (24)

2) Для вычисления угла между ребром и граньюАВСзапишем сначала каноническое уравнение ребра

.

Уравнение прямой :.

Координаты направляющего вектора вдоль . Координаты нормалинайдены выше (24).

.

.

3) Уравнение прямой :

.

После упрощения имеем - .

Координаты направляющего вектора вдоль -.

4) Найдем уравнение высоты, опущенной из вершины на грань АВС, уравнение которой получено ранее в (24).

Так как , то возьмем вектор, тогда уравнение высоты.

5) Решив систему уравнений

,

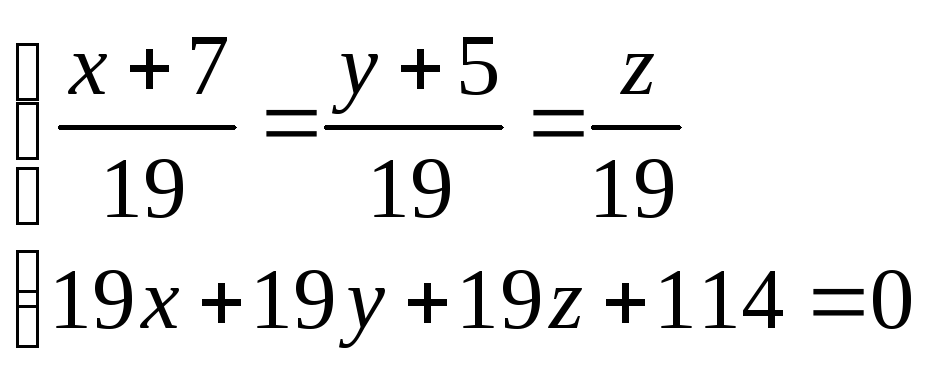найдем точку К, которая будет являться основанием высоты, опущенной из вершины D на грань АВС.

Для этого запишем уравнение прямой в параметрическом виде

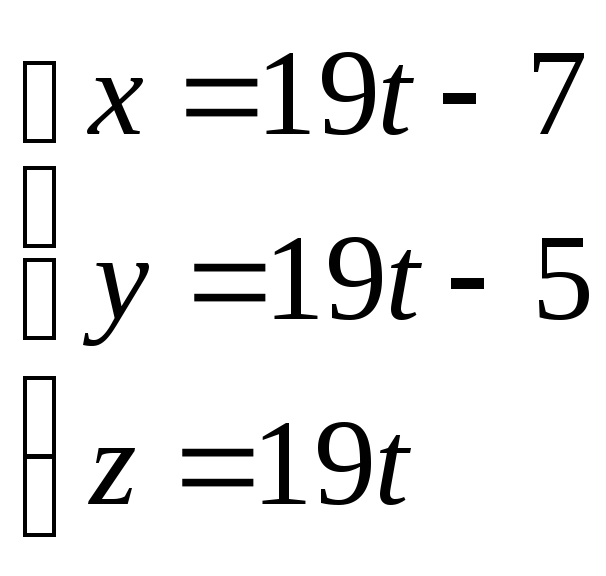, . (25)

Подставим в уравнение плоскости вместо переменных x, y, z их выражения через параметр :

,

, . (26)

Теперь из (25) найдем x, y, z.

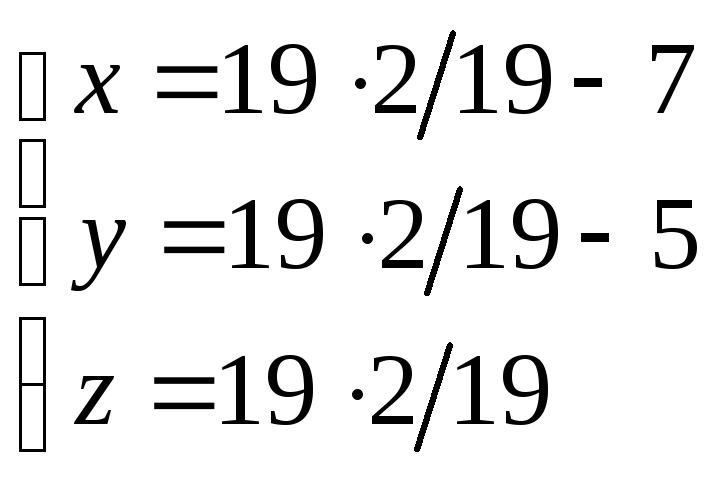, т. К {-5; -3; 2}.