
- •Министерство образования и науки российской федерации
- •Введение
- •Методические указания, примеры выполнения заданий задание 1
- •Решение системы методом определителей.
- •Решение систем матричным методом.
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задание 10
- •Задание 11
- •Учебное Пособие для выполнения контрольной работы № 1 по математике
- •394036 Воронеж, пр. Революции, 19.
Задание 2
При выполнении второго задания контрольной работы необходимы следующие понятия векторной алгебры.
Вектором
называется направленный отрезок. Вектор
![]() ,
заданный координатами начала
,
заданный координатами начала![]() и конца
и конца![]() имеет проекции, равные разностям
координат его конца и начала:
имеет проекции, равные разностям
координат его конца и начала:
![]()
Его
длина (модуль) определяется по формуле
![]() .
.
Проекция
одного вектора
![]() на направление другого
на направление другого![]() равна скалярному произведению этих
векторов, деленному на модуль второго
вектора:
равна скалярному произведению этих
векторов, деленному на модуль второго
вектора:
![]()
В координатной форме формула выглядит следующим образом:
![]() .
.
Угол
между положительными направлениями
векторов
![]() и
и![]() находится по формуле:
находится по формуле:
![]() ,
,
Значение
![]() можно не искать в таблицах, а дать ответ
в виде:
можно не искать в таблицах, а дать ответ
в виде:
![]() ,
,
Площадь треугольника АВС вычисляется при помощи векторного произведения по формуле:
![]() ,
,
где
![]() – векторное произведение.
– векторное произведение.
Пусть
![]() и
и![]() .
Найдем их векторное произведение по
формуле:
.
Найдем их векторное произведение по
формуле:
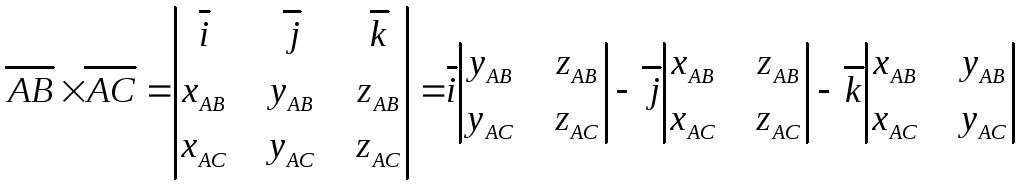
Вычислим
длину вектора
![]() и возьмем ее половину, которая и будет
численно равна искомой площади.
и возьмем ее половину, которая и будет
численно равна искомой площади.
Объем пирамиды вычисляется как одна шестая абсолютной величины смешанного произведения трех векторов, на которых построена пирамида.
Пусть
![]() ,
,![]() ,
,![]() .
Следует обратить внимание, что все три
вектора
.
Следует обратить внимание, что все три
вектора
![]() и
и
![]() здесь выходят из одной точки А.
здесь выходят из одной точки А.
Их смешанное произведение равно:
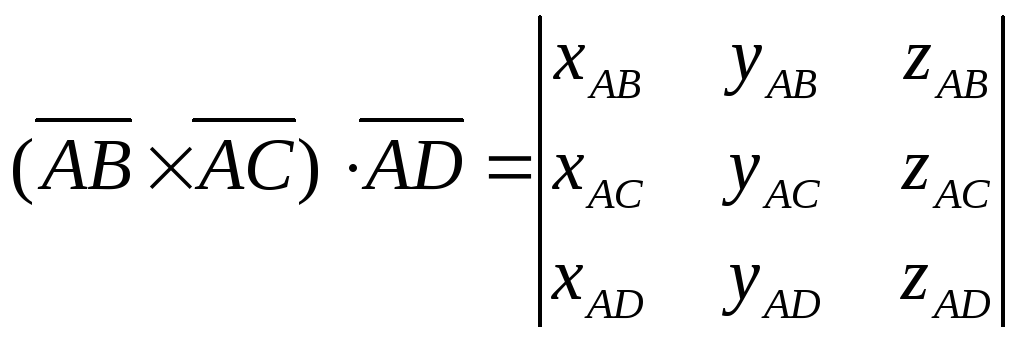 .
.
Объем
пирамиды
![]() будет равен одной шестой абсолютной
величины произведения векторов:
будет равен одной шестой абсолютной
величины произведения векторов:
![]() .
.
Пример.
Даны координаты вершин пирамиды
![]() ,
,![]() ,
,![]() ,
и
,
и![]() .
Надо средствами векторной алгебры
найти: 1) длину ребра
.
Надо средствами векторной алгебры
найти: 1) длину ребра![]() 2) проекцию
2) проекцию![]() на
на![]() ;
3) угол между ребрами
;
3) угол между ребрами![]() и
и![]() ;
4) площадь грани
;
4) площадь грани![]() ;
5) объем пирамиды
;
5) объем пирамиды![]() .
Сделать чертёж.
.
Сделать чертёж.
Решение: Сначала выполним чёртёж.

1)
Найдем координаты вектора
![]()
![]() ,
тогда длина ребра
,
тогда длина ребра
![]() равна
равна![]() .
.
2)
Найдем координаты векторов
![]() и
и![]() .
.
![]() ;
;
![]() .
.
Вычислим
проекцию
![]() на
на![]() :
:
![]() .
.
3)
Найдем
![]() .
Для этого вычислим координаты вектора
.
Для этого вычислим координаты вектора![]() (координаты
вектора
(координаты
вектора
![]() были получены
ранее):
были получены
ранее):
![]() ,
,
![]() ,
,
![]() ,
,
![]()
4)
Для вычисления площади грани
![]() возьмем любые два вектора, которые
образуют эту грань, например
возьмем любые два вектора, которые
образуют эту грань, например
![]() и
и
![]() .
Координаты вектора
.
Координаты вектора
![]() .
.
Найдем
векторное произведение
![]()
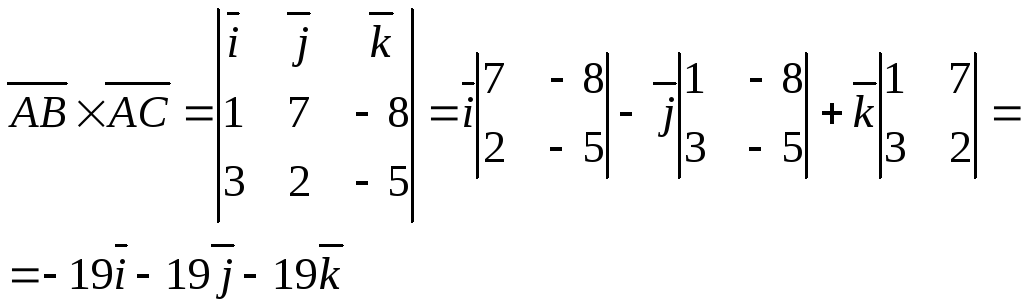
![]() ед2.
ед2.
5).
Координаты векторов
![]() ,
,![]() и
и![]() найдены выше. Вычислим их смешанное
произведение:
найдены выше. Вычислим их смешанное
произведение:
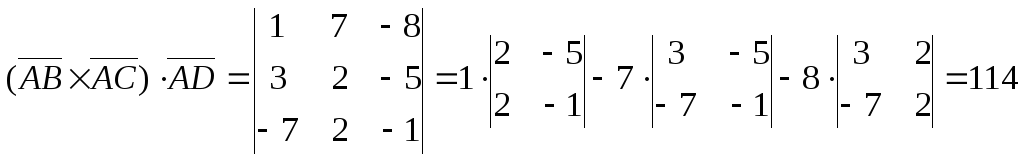
Объем
пирамиды равен
![]() ед3.
ед3.
Задание 3
Для
выполнения третьего задания рассмотрим
линии первого порядка
![]() – уравнение прямой в общем виде.
– уравнение прямой в общем виде.
Уравнение
прямой, проходящей через сторону АВ
треугольника АВС,
найдем как уравнение прямой, проходящей
через две точки
![]() и
и![]() :
:
![]() .
.
Аналогично
найдем уравнения сторон
![]() и
и![]() .
.
Чтобы
написать уравнение медианы
![]() ,
вспомним, что точка
,
вспомним, что точка![]() делит
сторону
делит
сторону![]() пополам. Найдем координаты точки
пополам. Найдем координаты точки![]() .
Если
.
Если![]() ,
,![]() ,
,![]() и
и![]() ,
то
,
то
![]() ,
,
![]() .
.
Теперь
осталось только записать уравнение
прямой
![]() ,
проходящей через две точки
,
проходящей через две точки![]() и
и![]() .
.
Высота
![]() перпендикулярна стороне
перпендикулярна стороне![]() .
Через
.
Через![]() проведем прямую с угловым коэффициентом
проведем прямую с угловым коэффициентом![]() :
:
![]() .
(19)
.
(19)
Так
как
![]() ,
то из условия перпендикулярности двух
прямых имеем
,
то из условия перпендикулярности двух
прямых имеем
![]() .
(20)
.
(20)
Запишем
уравнение стороны
![]() в виде с угловым коэффициентом
в виде с угловым коэффициентом
![]() .
.
Из
этого уравнения определим
![]() ,
а из (20) найдем
,
а из (20) найдем![]() .
Зная угловой коэффициент прямой
.
Зная угловой коэффициент прямой![]() из (19) получим уравнение перпендикуляра
из (19) получим уравнение перпендикуляра![]() .
.
Длину
высоты найдем как расстояние от точки
![]() до прямой
до прямой![]() по формуле:
по формуле:
![]() ,
,
где
![]() – уравнение стороны
– уравнение стороны![]() .
.
Чтобы
найти внутренние углы треугольника
![]() нужно угловые коэффициенты сторон
выписать в порядке убывания:
нужно угловые коэффициенты сторон
выписать в порядке убывания:![]() ,
затем вычислить тангенсы углов по
формулам:
,
затем вычислить тангенсы углов по
формулам:
![]() ,
,
![]() ,
,![]() .
.
Пример.
Даны координаты вершин треугольника:
![]() .
Требуется найти: 1) уравнение сторон
треугольника; 2) уравнение медианы
.
Требуется найти: 1) уравнение сторон
треугольника; 2) уравнение медианы![]() ;
3) длину и уравнение высоты
;
3) длину и уравнение высоты![]() ;
4) внутренние углы треугольника
;
4) внутренние углы треугольника![]() .
.
Решение:
1)
Найдем уравнение стороны
![]() :
:![]() .
Запишем уравнение в общем виде:
.
Запишем уравнение в общем виде:![]() .
.
Найдем
уравнение
![]() :
:![]() или
или![]() .
.
Найдем
уравнение
![]() :
:![]() ;
т. е.
;
т. е.![]() .
.
2)
Найдем координаты точки
![]() :
:
![]() ;
;
![]() ;
;![]() .
.
Запишем
уравнение
![]() :
:
![]() ,
или
,
или
![]() .
.
3) Найдем длину высоты АК
![]() .
.
Придадим
уравнению прямой ВС
форму уравнения с угловым коэффициентом
![]() ,
откуда
,
откуда![]() .
.
Угловой
коэффициентом прямой АКравен
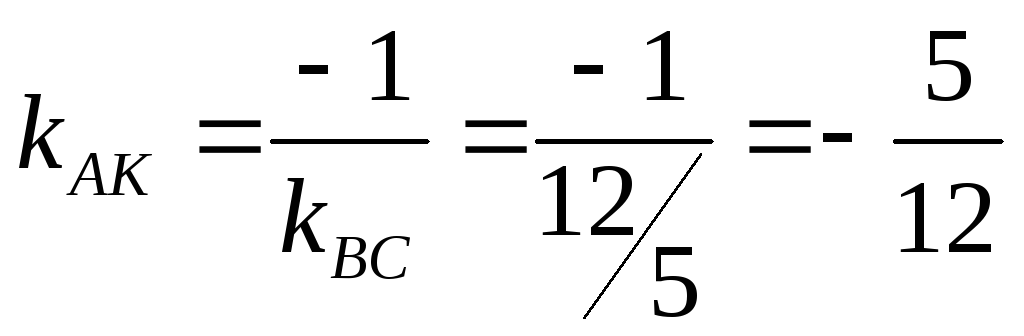 .
.
Уравнение
(АК):
![]() ;
;
![]() ;
;
![]() .
.
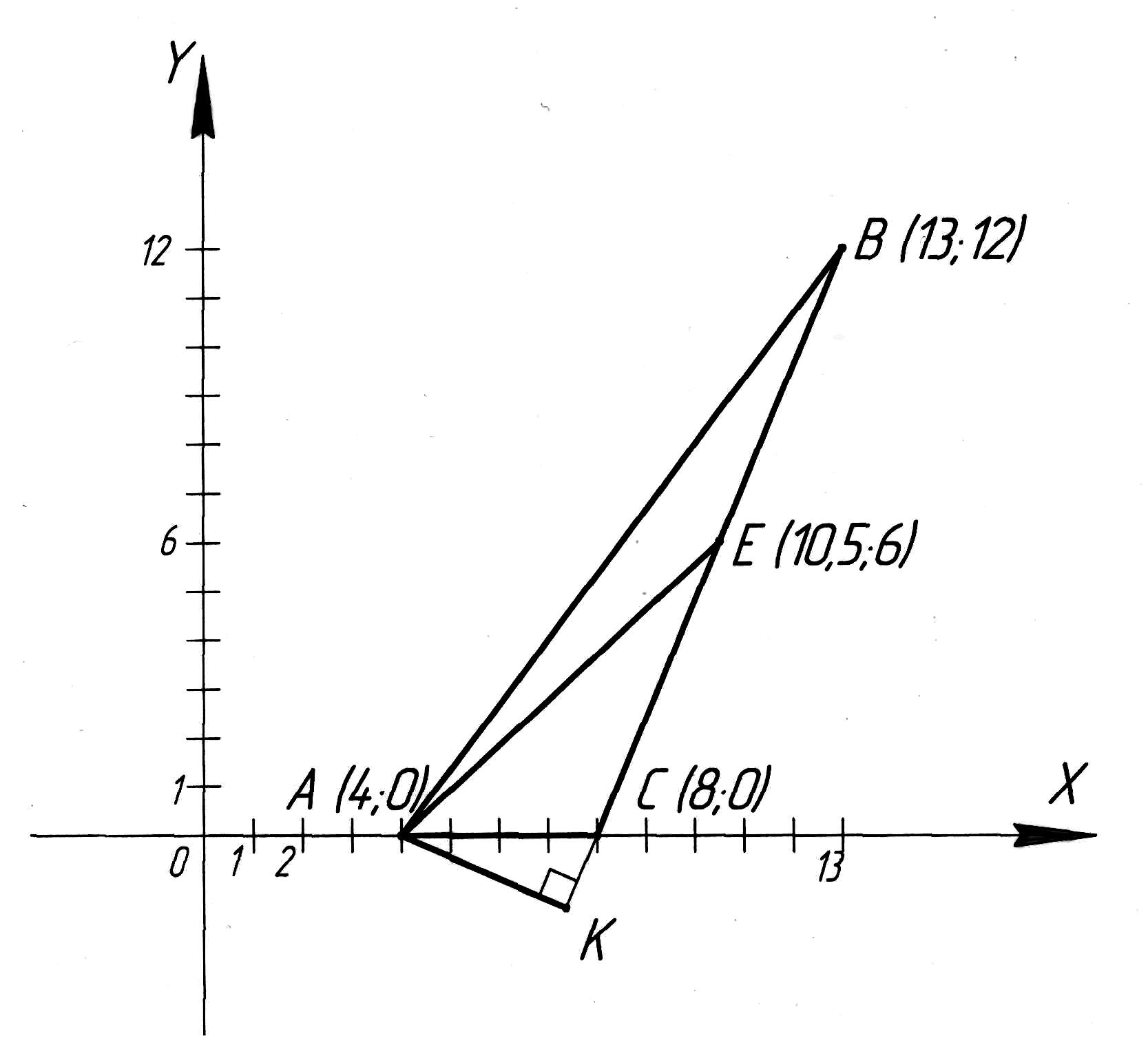
Рис. 1. Чертеж к заданию 3.
4) Запишем уравнения сторон треугольника в виде уравнений прямых с угловыми коэффициентом:
(АС):
![]() ,
,![]() .
.
(АВ):
![]() ,
,![]() .
.
(ВС):
![]() ,
,![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
