7. Исследование кинетики гомогенных химических реакций. Реакторы периодического действия с постоянным и переменным объемом реакционной массы, реакторы идеального вытеснения.

Кинетику реакции исследуют в реакторах смешения периодического действия (РИС-П).

В реакторе устанавливается и поддерживается заданная температура. Далее вводится рассчитанное количество исходных реагентов и интенсивно перемешивается (начало эксперимента).

В определенные промежутки времени отбираются пробы и анализируются. По найденным значениям строится концентрационная зависимость.

В дальнейшем эта зависимость обрабатывается интегральным или дифференциальным методами.

Интегральный метод (уравнение скорости).

;

Разделим переменные:

Результатом интегрирования левой части уравнения будет: - уравнение прямой линии в координатах.

F(Ci(j))

После нахождения концентрационной зависимости задаются функцией

Дифференциальный метод

1 – на концентрационной зависимости выбирается произвольно несколько точек;

2 – к выбранным точкам проводят касательные и по углу наклона определяют истинную скорость;

3 – задаются уравнением скорости и строят график зависимости.

Расчет химического реактора достаточно сложен и трудоемок и включает в себя выбор модели реактора, технологический, конструктивно-механический расчеты. Сложность задачи расчета реакторов зависит от многих факторов: типа химической

реакции, ее термодинамики, скорости теплообмена с окружающей средой, распределения вещества и тепла по объему.

В ряде случаев осуществляют расчет специальных устройств, входящих в конструкцию реактора: барботеров, теплообменников, змеевиков, циклонов и других. Однако в рамках изучаемой дисциплины расчет реактора будет заключаться в выборе модели реактора и нахождении его размеров, необходимых для получения заданного количества целевого продукта.

Для достижения этой цели используют расчетные уравнения, устанавливающие функциональную зависимость времени пребывания реагентов (время реакции) в реакторе () от различных факторов:

 = f (x, с_o, _r), (1)

где x - заданная степень превращения; с_o - начальная концентрация исходного реагента; _r - скорость химической реакции.

Определив время, необходимое для проведения процесса, можно рассчитать объем реактора и его основные размеры для заданной производительности.

Расчетные уравнения для различных типов реакторов:

_{- реактор идеального смешения непрерывного действия, РИС-Н:}

для непрерывных реакторов пользуются понятием условного времени пребывания реагентов в реакторе, которое определяется по уравнению:

(2)

где, - условное время пребывания, одинаковое для всех частиц;V - объем реактора; G_V,0 - объемный поток реагента, поступающего в реактор.

Зависимость объемного потока G_V,0 от мольного потока G_n,0 реагентов имеет вид:

G _n,0 = G_V,0 · с _i,0 (3)

_{- реактор идеального вытеснения, РИВ:}

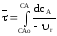; (4)

- реакторы идеального смешения периодического действия, РИС-П

(при V=const, ε=0):

(5)

- РИС-П (при V≠ const, ε≠ 0):

, (6)

где n _i,0 - начальное число молей реагента, ε- коэффициент относительного изменения объема реакционной массы, которая равна:

, (7)

где V _x=1,V _x=0 – мольные объемы реакционной массы при степени превращения, равной 1 и 0.

Для реакций нулевого, первого и второго порядка эти уравнения сравнительно легко решаются аналитически. Следует отметить, что уравнения для реакций второго порядка легко решаются в случае реакций с одним реагентом или с двумя реагентами при их эквимолярном соотношении на входе в реактор, то есть для реакций типа:

2 А  С или А + В  С (при С_А,0 = С_В,0 ).

В случае реакций, описываемых более сложными кинетическими уравнениями, можно пользоваться методом графического интегрирования. Для этого строят график зависимости в координатах 1/^_r = f (x_i), вычисляют площадь, ограниченную кривой, осью абсцисс и соответствующими пределами изменения x_i, отложенной по этой оси. При этом площадь под этой кривой (S) будет равняться интегралу , а время химической реакции произведению:

. (8)

В то же время, если известно время химической реакции, объем РИС-П можно найти, используя уравнение:

(9)

где G - суточная производительность; Z-запас мощности (0,1-0,15); φ-коэффициент заполнения (0,6 - 0,85); m- количество реакторов;

_пол - полное время периодического процесса.

Это время складывается из времени химической реакции _х.р и вспомогательного _всп, расходуемого на загрузку реагентов, выгрузку продуктов и др.:

_пол = _х.р + _всп (10)

Для определения объема реактора обычно задаются производительностью, а время пребывания рассчитывают по приведенным выше уравнениям, справедливым для данного типа реактора, после чего определяют объем реактора.

Для проточных реакторов идеального смешения соединенных в каскад (К-РИС-Н) используют графический и аналитический методы расчета

Графический метод расчета. Этот метод прост и позволяет рассчитать каскад реакторов идеального смешения непрерывного действия для реакции любого порядка.

В основе расчета лежит уравнение (2)

, (11)

где с_{i, m-1} - концентрация реагента на входе в m-ый реактор;

с_{i, m}- концентрация реагента на выходе из m-го реактора.

Из уравнения (11) находим, что

(12)

Как видно из уравнения (12), для m-го реактора зависимость скорости реакции от концентрации изображается в виде прямой с углом наклона, для которого (рис. 1). С другой стороны, скорость реакции описывается уравнением

, (13)

которое на графике в координатах 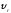отпредставляет собой приn>1 параболу, а при n = 1 прямую линию. Точка пересечения линии уравнений (11) и (8.12) характеризует концентрацию реагента в m-ом реакторе.

Для расчета К-РИС-Н графическим методом необходимо:

1. Вначале построить по уравнению зависимости _r от С_i (11).

2. Затем из точки, лежащей на оси абсцисс, для которой , провести прямую с тангенсом угла наклона, равным, до пересечения с кривой (прямой) в точке М.

3. Опустив перпендикуляр из точки пересечения М на ось абсцисс, получают значение концентрации реагента на выходе из первого реактора. Эта же концентрация является исходной для второго реактора.

4. Для нахождения концентрации во втором реакторе операцию повторяют, взяв за исходную точку , и т. д. до тех пор, пока в последнем реакторе не будет достигнута заданная концентрация. При этом число ступеней и будет числом реакторов в каскаде, необходимым для достижения заданной степени превращения.

М

Е

Д

Рис. 8.1. Графический метод расчета каскада реакторов идеального смешения

Аналитический метод расчета. Аналитический метод расчета используется только для химических реакций первого порядка.

Для этого используют уравнение:

, (14)

Уравнение (14) устанавливает зависимость m от отношения , которое выражает степень переработки реагента и величины, пропорциональной объему каждого реактора в каскаде.