
- •Примеры базисов
- •Интегрирование
- •Определение
- •Аддитивная граница
- •25. Вероятность ошибки при оптимальном приеме в канале со случайной фазой
- •26. Относительная фазовая модуляция
- •27. Распределения Релея и Райса
- •28. Канал с замираниями. Модель с рассеивателями
- •32. Каналы с межсимвольной интерференцией. Оптимальный прием
- •Литература
11. Вероятность ошибки при оптимальном приеме дискретных сигналов
Вероятность ошибки может быть найдена как
q−1 |
|
Pe = ∑Pe (i)Pi , |
(11.1) |
i=0 |
|
где Pe (i) – вероятность ошибки при передаче i -го сигнала, |
Pi – вероятность |
передачи i -го сигнала. Выражение (11.1) дает точное значение вероятности ошибки. В ряде случаев воспользоваться этим выражением не удается, так как
невозможно точно вычислить условные вероятности Pe (i) . В этом |
случае |
приходится пользоваться верхней оценкой вероятности ошибки |
|
q−1 ~ |
|
Pe ≤ ∑Pe (i)Pi , |
(11.2) |
i=0 |
|
~ ≥
где Pe (i) Pe (i) верхняя оценка условной вероятности ошибки. Для вычисления этой оценки существует ряд подходов. Рассмотрим некоторые из них.
Аддитивная граница (аддитивное неравенство, неравенство Буля, граница объединения). Условная вероятность ошибки при передаче i -го сигнала определяется как
Pe (i) = Pr[i ≠ i | i] .
Используя понятие решающей области, виде
Pr[i) ≠ i | i] = Pr[r Ri
это выражение можно переписать в
q−1 |
|
|
|
| i]= Pr U{r Rk |
| i} . |
(11.3) |
|
|
k =0 |
|
|
k ≠i |
|
||
|
|
|
|
Аддитивное неравенство позволяет оценить сверху вероятность объединения любых событий. Оно записывается как
|
|
|
≤ ∑Pr[ Ai ] , |
(11.4) |
Pr UAi |
||||
|
i |
|
i |
|
где {Ai } множество некоторых событий. Применяя (11.4) к (11.3), получим
Pr[i) |
q−1 |
|
≠ i | i] ≤ ∑Pr[r Rk | i] . |
(11.5) |
k =0 k ≠i

Вероятность Pr[r Rk | i] в свою очередь может быть оценена сверху вероятностью ошибки в системе передачи, использующей только два сигнала
s |
(t) и s |
k |
(t) . |
В такой системе существуют только две решающие области R(2) |
|||||||||
i |
|
|
|
|
|
|
|
|
|
i |
|
|
|
и |
R(2) 1), |
то есть R(2) |
UR(2) = R D и |
R(2) I R |
(2) . Очевидно, |
что R(2) |
R |
k |
, |
||||
|
k |
|
|
i |
k |
i |
k |
|
k |
|
|
||
поэтому Pr[r Rk | i] ≤ Pr[r Rk(2) | i] , далее |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
~ |
q−1 |
|
(2) |
| i] . |
|
|
|
|
|
|
|
|
|
Pe (i) ≤ Pe (i) = |
∑Pr[r Rk |
|
|
|
|
|||
|
|
|
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
k ≠i |
|
|
|
|
|
|
|
Вычисление |
вероятности Pr[r Rk(2) |
| i] |
обычно |
оказывается |
сравнительно |
||||||||
несложным в отличие от вероятности Pr[r Rk |
| i] . Окончательное выражение |
||||||||||||
для аддитивной границы вероятности ошибки имеет вид |
|
|
|
|
|||||||||
|
|
|
|
|
q−1 q−1 |
|
|
| i]Pi . |
|
|
|
|
|
|
|
|
|
|
Pe ≤ ∑∑Pr[r Rk(2) |
|
(11.6) |
||||||
i=0 k =0 k ≠i
□
Аппроксимация решающей области. Условная вероятность ошибки при передаче i -го сигнала определяется как
Pe (i) = Pr[i ≠ i | i] .
Используя понятие решающей области, это выражение можно переписать в виде
Pr[i) ≠ i | i] =1 − Pr[r Ri | i]=1 − ∫w(r | i)dr . |
(11.7) |
Ri |
|
Если интеграл в правой части равенства (11.7) вычислить не удается, то можно
оценить его снизу, |
используя подходящую аппроксимацию решающей области |
|
~ |
~ |
выбрана так, |
Ri . Пусть Ri Ri |
и конфигурация аппроксимирующей области Ri |
|
что интеграл ∫R~i w(r | i)dr вычисляется аналитически. Поскольку w(r | i) ≥ 0 для
всех r , так как это плотность вероятностей, то ∫R~ w(r | i)dr ≤ ∫R w(r | i)dr . |
||
|
i |
i |
Поэтому имеем верхнюю границуPe (i) ≤1 − ∫R~i |
w(r | i)dr и окончательно |
|
1 Верхний индекс 2 здесь означает, что в системе используется только два сигнала
q−1 |
|
Pe ≤1 − ∑Pi ∫~ w(r | i)dr . |
(11.8) |
i=0 Ri |
|
□
В завершение отметим, что для вычисления вероятности ошибки следует использовать, в тех случаях, когда это возможно, точное выражение (11.1), либо оценки, например, оценки (11.6) и (11.8). Во всех случаях для вычисления вероятности ошибки необходимо знать априорное распределение на входе канала {Pi }, условные функции плотности вероятности w(r | i) , описывающие канал, и алгоритм приема, то есть конфигурацию решающих областей.
Число двоичных единиц (бит) переносимых q -ичным сигналом равно
m = log2 q . При ошибке, происходящей при передаче сигналов, формируется ошибочное решение относительно номера переданного сигнала и возникает от
1 до m ошибочных бит. Рассмотрим вероятность ошибки на бит Pb , и ее связь с
вероятностью ошибки на символ Pe . Определим вероятность принятия решения в пользу сигнала с номером i' при условии, что был передан сигнал с номером
i , и обозначим ее |
как Pe (i,i') , |
i' ≠ i , |
то |
есть Pe (i,i') = Pr[r Ri' | i] . Тогда |
|||||
очевидно, чтоPe (i) = ∑iq'=−10,i'≠i Pe (i,i') . |
|
|
|
|
|
|
|||
Пусть |
n(i,i') |
- число разрядов, |
в |
которых различаются |
двоичные |
||||
представления |
номеров сигналов |
i |
и |
i' . Например, |
n(5,6) = 2 , |
так как |
|||
510 =1012 , 610 |
=1102 . Очевидно, |
что |
1 ≤ n(i,i') ≤ m при |
i' ≠ i . Тогда можно |
|||||
записать, что |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
q−1 q−1 |
|
|
|
||
|
|
Pb = |
∑∑Pe (i,i')n(i,i')Pi . |
|
|
||||
|
|
|
|
|
|||||
|
|
|
m i=0 |
i'=0 |
|
|
|
||
i'≠i
Вэтом равенстве фактически записано отношение среднего числа ошибочно принятых бит к их общему числу. Точное вычисление вероятности ошибки на бит может оказаться затруднительным. Основная проблема состоит
ввычислении, или достаточно точном оценивании, вероятностей Pe (i,i') . Тем
не менее, в ряде случаев сигналов она разрешима.
Заметим, что вероятность ошибки на бит может быть уменьшена, если назначить номера сигналов так, чтобы уменьшить величины произведений
Pe (i,i')n(i,i') . |
На практике |
часто оказывается, что значения вероятностей |
|
Pe (i,i') сильно различаются |
при различных i,i' . В частности это так при |
||
использовании АМ, |
ФМ, КАМ сигналов. Поэтому разумно назначить номера |
||
сигналов так чтобы |
величина n(i,i') была малой для тех пар (i,i') , для которых |
||
вероятность |
Pe (i,i') |
велика. В этом случае можно добиться, что произведения |
|
Pe (i,i')n(i,i') |
будут |
небольшими и общая вероятность ошибки на бит |
|
уменьшится. |
Такая нумерация может быть обеспечена с использованием кода |
||
Грея (Gray code).
Код Грея представляет собой переупорядочение двоичных кодовых последовательностей таким образом, что соседние последовательности
отличаются только в одном двоичном разряде. |
|
Простой пример приведен в |
||||
табл.11.1. |
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 11.1 |
|
Код Грея длины 3 |
|
|
|
||
|
|
|
|
|
|
|
|
Десятичное |
|
Двоичное |
|
Код |
|
|
представление |
|
представление |
|
Грея |
|
|
0 |
|
000 |
|
000 |
|
|
1 |
|
001 |
|
001 |
|
|
2 |
|
010 |
|
011 |
|
|
3 |
|
011 |
|
010 |
|
|
4 |
|
100 |
|
110 |
|
|
5 |
|
101 |
|
111 |
|
|
6 |
|
110 |
|
101 |
|
|
7 |
|
111 |
|
100 |
|
Из табл. 11.1 в частности |
следует, что |
n(5,6) =1, так как 510 =111Gray , |
||||
610 =101Gray . Это значит, что при |
ошибочном решении в пользу сигнала 6 при |
|||||
условии, что был передан сигнал 5, произойдет ошибка только в одном двоичном разряде, а не в двух как при обычной нумерации сигналов. Это значит, что применение кода Грея вместо обычной нумерации сигналов желательно, если вероятность Pe (5,6) велика.
Алгоритм построения кода Грея. Код Грея любой длины может быть
построен рекуррентно. Обозначим код Грея длины n как |
G(n) . Очевидно, что |
|
G(1) ={0,1} . |
Построение кода G(n +1) на основе кода |
G(n) выполняется |
следующим |
образом: |
|
|
~ |
~ |
а) Построение вспомогательного списка G(n) . Список |
G(n) |
|
представляет собой список G(n) , переупорядоченный в обратном порядке |
|
|
б) |
~ |
|
Построение кода Грея G(n +1) из G(n) и G(n) . К началу каждого |
||
слова из |
~ |
и оба |
G(n) приписывается 0, к словам из G(n) приписывается 1, |
||
|
~ |
|
списка слов объединяются, то есть G(n +1) = ((0g, g G(n)),(1g, g G(n))). |
|
|
Пример. Построение кода Грея длины 4. |
|
|
|
~ |
|
По определению G(1) ={0,1} . Тогда G(1) = (1,0) , и G(2) = (00,01,11,10) . |
||
|
~ |
= (10,11,01,00) , и G(3) = (000,001,011,010,110,111,101,100). |
Следовательно G(2) |
||
~ |
= (100,101,111,110,010,011,001,000) , и окончательно G(4) = (0000, |
|
Поэтому G(3) |
||
0001, 0011,0010,0110,0111,0101,0100,1100,1101,1111,1110,1010,1011,1001,1000).

12. Оптимальный прием в канале с аддитивным белым гауссовским шумом
Пусть {si (t)} - множество сигналов, используемых для передачи,
заданных на интервале [0,T ] , i = 0,1,..., q −1, {Pi }- |
априорное распределение, |
||||
заданное на этом |
множестве. |
Сигнал |
на выходе канала |
имеет вид |
|
r(t) = s(t) + n(t) , где |
s(t) {si (t)} , |
n(t) - аддитивный белый гауссовский шум |
|||
(АБГШ) со спектральной плотностью мощности |
N0 / 2 . Задача |
приемника |
|||
состоит в определении номера переданного сигнала |
i по принятому сигналу |
||||
r(t) . |
|
|
|
|
|
Выберем базис {ϕ j (t)}, j =1,..., D , |
для представления сигналов. Тогда |
||||
вместо множества сигналов {si (t)} можно рассматривать множество D -мерных вещественных сигнальных векторов (сигнальных точек) {si }, где si = (si1 ,..., siD )
и |
sij = (si ,ϕ j ) = ∫0T si (t)ϕ j (t)dt |
- скалярное произведение i −го сигнала и |
j -ой |
||||||
базисной |
функции, |
j =1,..., D . |
Аналогично можно построить разложение |
||||||
принятого |
сигнала |
r(t) |
|
по |
базисным |
функциям, |
r = (r1 ,..., rD ) , |
где |
|
rj |
= (r,ϕ j ) = ∫0T r(t)ϕ j (t)dt . |
Очевидно, что |
r = s +n , где |
n = (n1 ,..., nD ) |
и |
||||
n j |
= (n,ϕ j ) = ∫0T n(t)ϕ j (t)dt |
- |
скалярное произведение шума и j -ой базисной |
||||||
функции. |
Отметим, |
что случайные величины (с.в.) n j |
независимы между |
||||||
собой и имеют гауссовское распределение с нулевым математическим ожиданием, поскольку шум имеет нулевое среднее, и дисперсией N0 / 2 , то есть
n j = 0 , n2j = N0 / 2 , и n j nk = 0 , j, k = 0,1,..., D , j ≠ k . Эти свойства следуют из
свойств БГШ.
Для построения алгоритма оптимального приема нужно знать вид
условных плотностей |
вероятностей |
w(r | i) , |
определяемых |
каналом. |
При |
|||||||||||
условии, что передан i -й сигнал, |
r = si |
+ n , поэтому для канала с АБГШ |
|
|
|
|||||||||||
|
1 |
D |
|
|
2 |
|
|
1 |
D |
|
|
1 |
D |
|
|
|
|
|
|
r −si |
|
|
|
|
∑(rj − sij ) |
2 |
|
||||||
w(r | i) = |
|
|
exp − |
|
|
|
= |
|
|
|
− |
|
|
|
, |
|
|
N0 |
|
πN0 |
exp |
N0 |
|
|
|||||||||
|
πN0 |
|
|
|
|
|
|
|
j=1 |
|
|
|
||||
или w(r | i) = K exp(− d 2 (r, si ) / N0 ), где K = (πN0 )−D / 2 , d( , ) - евклидово
расстояние между точками из R D . Теперь можно записать выражение для решающих областей оптимального приемника МАВ
Ri( MAB) = r : Pi exp(− d 2 (r, si ) / N0 )= max Pk exp(− d 2 (r, sk ) / N0 ), |
|
|
|
0≤k≤q−1 |
|
или |
= min (d 2 (r, sk ) − N0 ln Pk ). |
|
Ri( MAB) = r : d 2 (r, si ) − N0 ln Pi |
(12.1) |
|
|
0≤k≤q−1 |
|
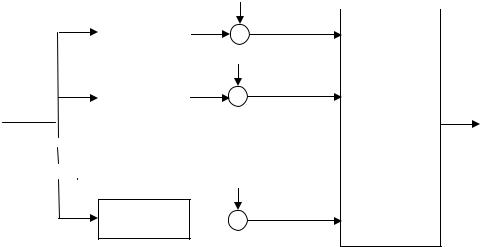
Схема приемника МАВ для канала с АБГШ показана на рис. 12.1
|
|
|
|
− N0 ln P0 |
|
|
|
|
|
|
|
|
|
|
d 2 (r, s0 ) |
+ |
|
|
||
|
|
|
|
|||
|
|
|
|
− N0 ln P1 |
|
|
|
|
|
|
|
||
r |
d 2 |
(r,s1 ) |
+ |
|
Выбор |
i |
|
|
|
|
минимума |
||
|
|
|
|
|
|
|
− N0 ln Pq−1
d 2 (r, sq−1 )  +
+
Рис.12.1 Схема оптимального приемника для канала с АБГШ (приемник по МАВ)
Решающие области МП имеют вид
Ri( MП) = r : exp(− d 2 (r, si ) / N0 )= max exp(− d 2 (r, sk ) / N0 ), |
|
||||
|
|
0≤k≤q−1 |
|
|
|
или |
|
|
|
|
|
R( MП) = r : d(r, s |
) = min d(r, s |
k |
) . |
(12.2) |
|
i |
i |
0≤k ≤q−1 |
|
|
|
|
|
|
|
|
|
Последнее равенство означает, что прием по МП в канале с АБГШ эквивалентен приему по минимуму евклидова расстояния. Схема приемника МП для канала с АБГШ показана на рис. 12.2
|
|
d 2 (r,s0 ) |
|
|
|
|
|
|
|
Выбор |
|
|
|
|
|
|
|
r |
|
d 2 |
(r,s1 ) |
i |
|
|
|
|
минимума |
|
|
|
|
|
|
||
d 2 (r, sq−1 )
Рис.12.2. Схема оптимального приемника для канала с АБГШ (приемника по МП)
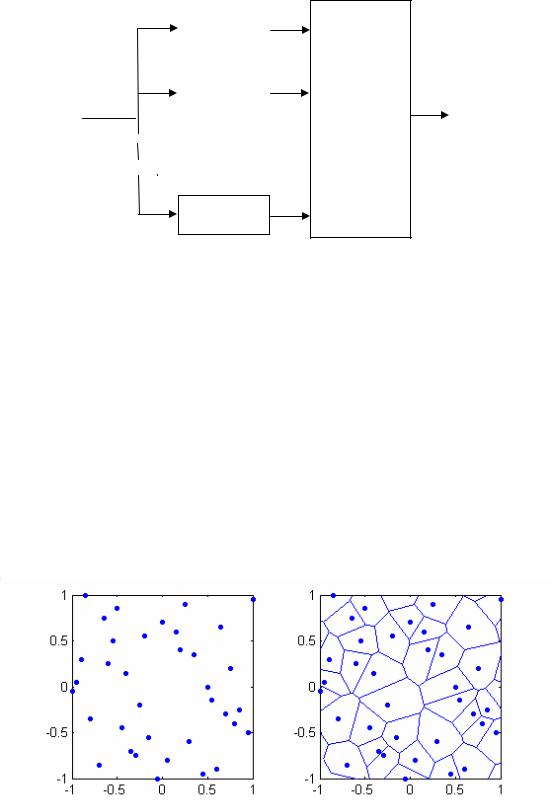
Решающая область Ri , заданная равенством (12.2), представляет собой
множество точек из R D , лежащих ближе к si , чем к любой другой сигнальной точке sk , k ≠ i . Для случая D = 2 эти области представляют собой выпуклые многоугольники и известны как области Вороного. На рис.12.3 показано для примера некоторое произвольное двумерное сигнальное созвездие и соответствующее ему разбиение на решающие области (области Вороного).
Рис.12.3 Сигнальное созвездие и разбиение на решающие области (области Вороного).
На вход схем, показанных на рис.12.1 и 12.2 , подается вектор r , полученный в результате конечномерного представления выходного сигнала канала r(t) . Рассмотрим более подробно как выглядит приемник,
обрабатывающий выходной сигнал канала r(t) . Поскольку конечномерное представление сохраняет расстояние, то
d 2 (r, si ) = d 2 (r(t), si (t)) = T∫(r(t) − si (t))2 dt = T∫r 2 (t)dt − 2T∫r(t)si (t)dt + Ei ,
0 0 0
где Ei = ∫0T si2 (t)dt – энергия i -го сигнала. Тогда равенства (12.1) и (12.2) можно переписать в виде
Ri( MAB) = |
|
T |
|
|
max |
T |
|
, |
(12.3) |
r : ∫r(t)si (t)dt −Ci( МАВ) = |
∫r(t)sk (t)dt −Ck( МАВ) |
|
|||||||
|
|
0 |
|
|
0≤k≤q−1 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
где C (МАВ) = (E |
k |
− N |
0 |
ln P ) / 2 , k = 0,1,..., q −1, |
|
|
|
|
|
k |
|
i |
|
|
|
|
|
||
T
Ri( MП) = r : ∫r(t)si (t)dt −Ci( МП)
0
|
T |
|
= |
0max≤k≤q−1 |
∫r(t)sk (t)dt −Ck( МП) |
|
|
0 |
, (12.4)
где Ck(МП) = Ek / 2 . Как видно из определения областей (12.3) и (12.4),
решения по МАВ и по МП строятся почти одинаково, разница состоит лишь в
постоянных Ck( МАВ) и Сk( МП) . |
На |
рис 12.4 показана схема оптимального |
||||||
приемника. Эта схема эквивалентна ранее приведенным схемам. |
|
|||||||
|
s0 (t) |
|
|
|
−C0 |
|
|
|
|
|
T |
|
|
|
|||
|
× |
|
|
∫dt |
+ |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
s1 (t) |
|
|
|
|
−C |
Выбор |
|
|
|
|
|
|
||||
|
|
|
T |
|
|
|||
r(t) |
|
|
|
|
1 |
i |
||
|
|
|
|
|
|
|||
× |
|
|
∫dt |
|
|
максимума |
||
|
|
+ |
|
|
||||
|
|
|
|
|
||||
|
|
|
|
0 |
|
|
|
|
|
sq−1 (t) |
|
|
|
−Cq−1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
T |
|
|
|
||
|
× |
|
|
∫dt |
+ |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.12.4. Схема оптимального (корреляционного) приемника для канала с АБГШ

Приемник, показанный на рис.12.4 называется корреляционным, так как структура, приведенная на рис 12.5, называется коррелятором.
|
si (t) |
|
|
r(t) |
T |
||
|
|||
|
∫dt |
||
× |
|
||
|
|
0 |
|
|
|
|
Рис.12.5. Коррелятор
Еще одна эквивалентная приведенным структура оптимального приемника может быть получена с использованием так называемых согласованных фильтров. Фильтр называется согласованным с сигналом si (t) ,
если его импульсная переходная характеристика равна hi (t) = si (T −t).
Рассмотрим реакцию фильтра, согласованного с сигналом si (t) , на сигнал r(t)
∞ |
∞ |
|
t1 = T −t +τ |
|
|
|
|
||||
yi (t) = ∫r(τ)hi (t −τ)dτ = |
∫r(τ)si (T −t +τ)dτ = |
|
τ = t1 −T + t |
|
= |
−∞ |
−∞ |
|
dτ = dt1 |
|
|
|
|
|
|
|
= ∞∫r(t1 −T + t)si (t1 )dt1 .
−∞
Отсюда следует, что yi (t) t =T = yi (T ) = ∞∫r(t1 )si (t1 )dt1 . Это значит, что значение
−∞
на выходе согласованного фильтра, взятое в момент t = T , равно значению на выходе коррелятора. Поэтому оптимальный приемник может быть построен по схеме с согласованными фильтрами и следующими за ними устройствами взятия отсчетов (см. рис.12.6)
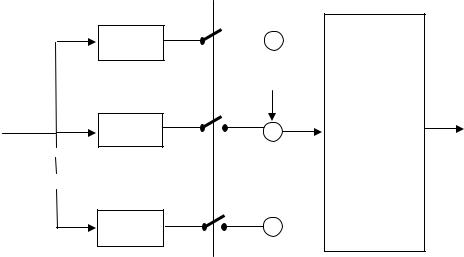
h0 (t)
r(t)
h1 (t)
hq−1 (t)
 −C0
−C0
 +
+ 
|
−C1 |
Выбор |
i |
|
|
||
|
|
максимума |
|
+ |
|
|
|
|
|
|
 −Cq−1
−Cq−1
+ 
t = T
Рис.12.6. Схема приемника с согласованными фильтрами для канала с АБГШ
Свойства согласованного фильтра. Предположим, что имеется некоторый фильтр с конечной импульсной переходной характеристикой h(t) , 0 < t < T . Пусть на его вход поступает сигнал r(t) = s(t) + n(t) , где s(t) -
полезный сигнал, а n(t) - АБГШ. Покажем, что если фильтр h(t) согласован с сигналом s(t) , то отношение сигнал/шум на выходе фильтра будет
максимальным.
Рассмотрим сигнал на выходе фильтра (символ , как и ранее, обозначает свертку)
y(t) = r(t) h(t) = ∞∫r(τ)h(t −τ)dτ = ∞∫s(τ)h(t −τ)dτ + ∞∫n(τ)h(t −τ)dτ .
−∞ −∞ −∞
Поскольку импульсная переходная характеристика фильтра h(t) равна нулю вне интервала (0,T ) то можно записать, что
|
y(t) = ∫t |
s(τ)h(t −τ)dτ + ∫t |
n(τ)h(t −τ)dτ = sh (t) + nh (t) , |
|
|
t −T |
t−T |
||
где sh (t) = ∫t |
s(τ)h(t −τ)dτ , |
nh (t) = ∫t |
n(τ)h(t −τ)dτ - сигнальная и шумовая |
|
t−T |
|
t−T |
||
составляющие сигнала на выходе фильтра соответственно. Обозначим
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
рассмотрим |
значение |
отсчета |
сигнала |
на выходе фильтра, |
||||||||||
h (t) = h(t −T ) |
|||||||||||||||||||||||||||||||
взятого в момент t = T . Оно равно |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
~ |
T |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(t) |
|
t=T = y(T ) = ∫s(t)h (t)dt + |
∫n(t)h (t)dt , |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
~ |
|
(12.5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(T ) = sh (T ) + nh (T ) = (s, h ) + |
(n, h ) , |
|||||
где через |
|
( , ) |
|
|
|
обозначено скалярное |
произведение функций, |
~ |
|||||||||||||||||||||||
|
|
|
|
sh (T ) = (s, h ) - |
|||||||||||||||||||||||||||
отсчет сигнальной составляющей на выходе фильтра, |
nh (T ) = |
~ |
|||||||||||||||||||||||||||||
(n, h ) - отсчет |
|||||||||||||||||||||||||||||||
шумовой составляющей на выходе фильтра. |
Величина nh (T ) |
представляет |
|||||||||||||||||||||||||||||
собой гауссовскую случайную величину с нулевым средним |
и дисперсией |
||||||||||||||||||||||||||||||
(N0 / 2) |
|
~ |
|
|
|
2 |
|
= (N0 / 2) |
|
h |
2 |
. |
|
|
|
|
|
|
|||||||||||||
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
В |
|
дальнейшем рассмотрении |
будет |
использовано |
неравенство |
||||||||||||||||||||||||||
( f , g)2 ≤ |
|
|
|
f |
|
|
|
2 |
|
|
|
g |
|
|
|
2 , |
|
известное |
как неравенство Коши-Шварца-Буняковского. |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Оно обращается в равенство, |
если функции f (t) и |
g(t) |
пропорциональны, то |
||||||||||||||||||||||||||||
есть если |
f (t) = Cg(t) , где C - некоторая константа. |
|
|
|
|||||||||||||||||||||||||||
|
Легко видеть, что если положить |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
(12.6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h (t) = Cs(t) , |
|
|
|
||
то для величины квадрата сигнальной составляющей в равенстве (12.5) можно
с использованием |
неравенства |
Коши-Шварца-Буняковского |
записать, |
|
что |
|||||||||||||||||||||||||||
sh (T )2 = (s,Cs)2 = C 2 |
|
|
|
s |
|
|
|
4 = C 2 E 2 , |
где |
E |
- энергия сигнала. При этом условии |
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
дисперсия шумовой компоненты будет равна σh2 = (N0 / 2) |
|
|
|
Cs |
|
|
|
2 |
= (N0 / 2)C 2 |
|
|
|
s |
|
|
|
2 , |
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
а отношение этих величин будет равно своему максимальному значению |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
sh (T )2 |
= |
E |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(12.7) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
σh2 |
(N0 / 2) |
|||||||||||||||||||
Заметим, что значение константы C не играет роли, так как она присутствует в |
||||||||||||||||||||||||||||||||
числителе и |
знаменателе этого |
отношения. Поэтому в дальнейшем можно |
||||||||||||||||||||||||||||||
считать что |
C =1 . |
Из равенства (12.6) |
~ |
|
|
|
|
что |
||||||||||||||||||||||||
следует, что h(t) = s (t) = s(T −t) , |
|
|||||||||||||||||||||||||||||||
совпадает с определением согласованного фильтра.
Рассмотрим теперь свойства согласованного фильтра в частотной области. Обозначим через H ( f ) ↔ h(t) частотную характеристику фильтра.
Поскольку h(t) = s(T −t) , то
|
|
|
|
|
|
|
|
|
|
Замена |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
∞ |
∞ |
|
|
|
T −t = t |
|
∞ |
|
||||||||||||||||||||||
H ( f ) = ∫h(t)e− j 2πft dt = |
∫s(T −t)e− j 2πft dt = |
t = T −t1 |
= ∫s(t1 )e− j 2πf (T −t1 ) dt1 = |
|||||||||||||||||||||||||||
−∞ |
−∞ |
|
|
|
1 |
|
−∞ |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dt = −dt1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= e− j 2πfT ∫s(t1 )e j 2πft1 dt1 = e− j 2πfT S* ( f ) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где S( f ) - спектр сигнала. Спектр |
сигнальной |
составляющей |
на выходе |
|||||||||||||||||||||||||||
согласованного фильтра равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Sh ( f ) = S( f )H ( f ) = S( f )e− j 2πfT S * ( f ) = e− j 2πfT |
|
S( f ) |
|
2 . |
|
|||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
Тогда сама сигнальная составляющаяsh (t) ↔ Sh ( f ) равна |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
2 e j 2πft df , |
|
||||||||||||||||
|
|
|
sh (t) = ∫e− j 2πfT |
|
S( f ) |
|
|
|||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а ее отсчет в момент t = T будет равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
sh (T ) = ∞∫e− j 2πfT |
|
S( f ) |
|
2 e j 2πfT df = ∞∫ |
|
S( f ) |
|
2 df = ∞∫s2 (t)dt = |
|
|
|
s |
|
|
|
2 = E . |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
−∞ |
|
|
|
|
|
−∞ |
−∞ |
|
||||||||||||||||||||||
Здесь также использовано равенство Парсеваля. |
Отсюда следует, |
что как и |
||||||||||||||||||||||||||||
ранее, sh (T )2 = E 2 .
Шум на выходе согласованного фильтра окрашен и имеет спектральную плотность мощности
Nh ( f ) = (N0 / 2) H ( f ) 2 = (N0 / 2) S * ( f )e− j 2πfT 2 = (N0 / 2) S( f ) 2 .
Мощность шума на выходе фильтра (или дисперсия отсчета шума на выходе фильтра) равна, как и прежде,
∞ ∞ ∞
σh2 = ∫Nh ( f )df = (N0 / 2) ∫ S( f ) 2 df = (N0 / 2) ∫s2 (t)dt = (N0 / 2)
 s
s
 2 = (N0 / 2)E.
2 = (N0 / 2)E.
−∞ |
−∞ |
|
−∞ |
|
|
Следовательно получаем, что |
|
|
|
||
|
|
sh (T )2 |
= |
E |
, |
|
|
σh2 |
(N0 / 2) |
||
и это выражение совпадает с (12.7).

13. Вероятность ошибки при передаче двоичных сигналов в канале с аддитивным белым гауссовским шумом
Рассмотрим простой случай передачи двоичных сигналов. Вероятность ошибки определяется по формуле полной вероятности как
q−1
Pe = ∑Pe (i)Pi =Pe (0)P0 + Pe (1)P1 ,
i=0
где Pe (i) - условная вероятность ошибки при передаче i -го сигнала, Pi -
вероятность передачи i -го сигнала. Найдем сначала вероятность Pe (0) . Как следует из определения алгоритма приема по МП
Pe (0) = Pr[d 2 (r, s0 ) > d 2 (r,s1 ) | 0]= Pr[ |
|
r −s0 |
|
|
|
2 > |
|
|
|
r −s1 |
|
|
|
2 | 0] |
|
|
|
|
|
|
|
При передаче сигнала s0 (t) на выходе канала наблюдается r(t) = s0 (t) + n(t) , и
следовательно r = s0 +n . Тогда
Pe (0) = Pr[
 n
n
 2 >
2 > 
 s0 −s1 + n
s0 −s1 + n
 2 ]= Pr[
2 ]= Pr[
 n
n
 2 −
2 − 
 s0 −s1 + n
s0 −s1 + n
 2 > 0].
2 > 0].
Рассмотрим выражение 
 n
n
 2 −
2 − 
 s0 −s1 + n
s0 −s1 + n
 2 :
2 :
|
|
|
|
n |
|
|
|
2 − |
|
|
|
s0 −s1 + n |
|
|
|
2 = |
|
|
|
n |
|
|
|
2 − |
|
|
|
s0 −s1 |
|
|
|
2 − 2(s0 −s1 , n) − |
|
|
|
n |
|
|
|
2 = − |
|
|
|
s0 −s1 |
|
|
|
2 − 2(s0 −s1 , n) . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pe (0) = Pr[ξ > ∆2 ], |
|
(13.1) |
|||||||||||||||||||||||||||
где ξ = −2(s0 −s1 ,n) , |
|
|
|
|
∆2 = d 2 (s0 ,s1 ) = |
|
|
|
s0 −s1 |
|
|
|
2 – квадрат |
расстояния между |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
сигналами. Определим характеристики случайной величины ξ . Она равна |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ = −2(s0 −s1 ,n) = −2∑(s0 j − s1 j )n j , |
|
(13.2) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где s0 j , s1 j - координаты соответствующих сигнальных точек, |
|
n j - скалярные |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
произведения АБГШ |
|
|
|
|
и базисных функций. |
|
Величины n j |
это независимые |
||||||||||||||||||||||||||||||||||||||||||||||||||
одинаково распределенные гауссовские с.в. (см. свойства АБГШ) с параметрами n j = 0 , n2j = N0 / 2 . Найдем параметры величины ξ , определенной равенством
(13.2). Поскольку ξ представляет собой линейную комбинацию независимых
гауссовских с.в., то она тоже гауссовская. Далее, найдем математическое ожидание и дисперсию
|
|
|
|
|
D |
|
|
|
D |
|
|
|
|
|
|
|
ξ |
= − 2∑(s0 j − s1 j )n j = −2∑(s0 j − s1 j ) |
n j |
= 0 , |
|
|
|||||||
|
|
|
|
|
j=1 |
|
|
|
j=1 |
|
|
|||
|
D |
|
D |
|
|
|
|
D |
|
|
||||
D[ξ] = D − 2∑(s0 j − s1 j |
)n j = 4∑(s0 j − s1 j )2 D[n j ] = 2N0 ∑(s0 j − s1 j )2 =2N0 ∆2 . |
|||||||||||||
|
j=1 |
|
j=1 |
|
|
|
|
j=1 |
|
|
||||
Итак, |
вероятность Pe (0) вычисляется, как указано в (13.1), где ξ |
- |
||||||||||||
гауссовская с.в. с параметрами (0, 2N0 ∆2 ) . |
|
|
|
|
|
|
|
|||||||
Определим функцию |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
Q(x) = ∞∫ |
1 |
|
e−z2 / 2 dz . |
(13.3) |
||||
|
|
|
|
|
|
|
x |
2π |
|
|
|
|
|
|
Легко |
видеть, |
что |
Q(x) = Pr[ζ > x] , где ζ гауссовская |
с.в. |
с |
|||||||||
параметрами (0,1). С использованием функции (13.3) можно найти вероятность превышения некоторого порога A гауссовской с.в. X общего вида с
параметрами (m,σ 2 ) , то есть
Pr[ X > A] = Q Aσ− m .
С использованием (13.1) и (13.3) можно записать, что
P (0) |
|
2 |
|
|
∆ |
|
= Q |
∆ |
|
= Q |
. |
||
e |
|
2 |
|
|
2N0 |
|
|
|
∆ 2N0 |
|
|
|
Аналогичное значение имеет и вероятность Pe (1) , поэтому
P |
|
∆ |
|
(13.4) |
= Q |
|
. |
||
e |
|
2N0 |
|
|
|
|
|
|
Как следует из выражения (13.4), вероятность ошибки при передаче двоичных сигналов по каналу с АБГШ зависит только от евклидова расстояния между сигналами (но не от их конкретного вида!) и от интенсивности шума.
Функция Q(x) , используемая в выражении (13.4), не выражается через элементарные функции и вычисляется численно. На практике она может быть найдена из таблиц. Чаще, однако, в руководствах по теории вероятностей
встречаются таблицы значений гауссовской функции распределения, определенной как
F(x) = ∫x |
1 |
e−z2 / 2 dz . |
−∞ |
2π |
|
Связь между ней и функцией Q(x) задается равенством Q(x) =1 − F(x) . Часто встречаются также таблицы так называемой функции ошибок и дополнительной функции ошибок, определенных следующим образом
2π ∫0x e−z2 dz
и |
|
|
erfc(x) = |
2 |
∫x∞ e−z 2 dz =1 −erf(x) , |
|
π |
|
соответственно. Связь функции |
Q(x) с erfc(x) задается равенством |
|
Q(x) = erfc(x /  2 )/ 2 . Можно указать также просто вычисляемые верхние и
2 )/ 2 . Можно указать также просто вычисляемые верхние и
нижние границы для Q(x) для положительных значений ее аргумента
1 |
− |
1 |
−x2 / 2 |
< Q(x) < |
1 |
e |
−x2 / 2 |
, |
(13.5) |
|
1 |
e |
|
2π x |
|
||||||
2π x |
|
x2 |
|
|
|
|
|
|
|
|
и наиболее простую верхнюю границу |
|
|
|
|
|
|
|
|||
|
|
Q(x) ≤ |
1 |
e−x2 / 2 . |
|
|
|
|
(13.6) |
|
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
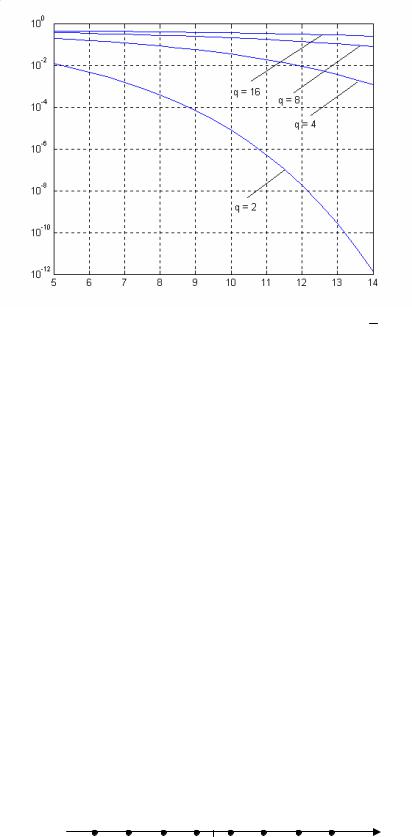
На рис.13.1а показан график функции Q(x) , а на рис.13.1б – графики этой функции, а также верхняя и нижняя границы (13.5) и простейшая верхняя граница (13.6) в полулогарифмическом масштабе.
|
Весьма точно значения Q(x) |
могут быть найдены с использованием |
|||||
приближенного выражения сравнительно удобного для программирования |
|||||||
|
|
|
5 |
|
1 |
i |
|
|
|
Q(x) ≈ f (x) |
∑ |
a |
, |
(13.7) |
|
|
|
|
|||||
|
|
|
i |
|
|
|
|
|
|
|
i=0 |
|
(1 + px) |
|
|
где |
f (x) = (1/ |
2π ) exp(−x2 / 2) , |
|
p = 0.2316419 , |
a = 0.3193815 , |
||
|
|
|
|
|
|
|
1 |
a2 |
= −0.3565638 , |
a3 =1.781478 , a4 = −1.821256 , a5 =1.330274 . Качество |
|||||
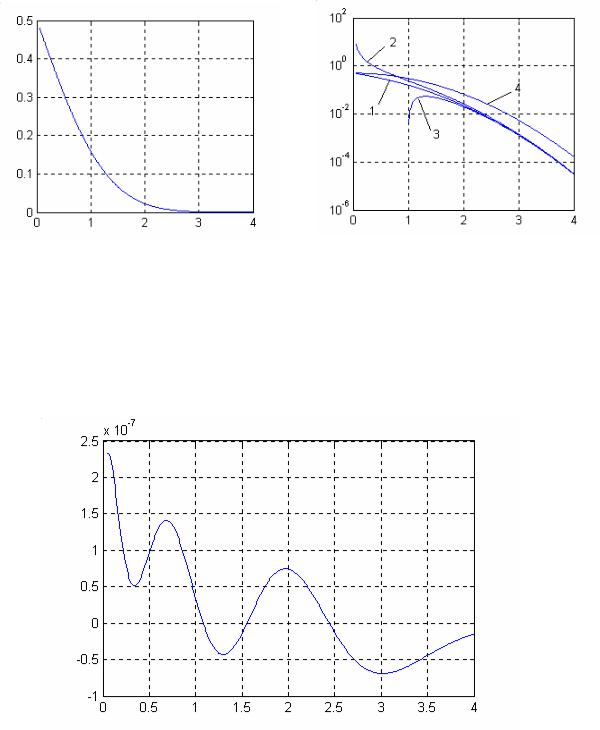
приближения иллюстрируется графиком рис.13.2, где показана разность между истинным значением Q(x) и приближением (13.7)
а |
б |
Рис.13.1 а) функция Q(x) , б) 1- функция Q(x) , 2,3 – верхняя и нижняя границы (13.5) , 4 – простая верхняя граница (13.6)
Рис.13.2 Ошибка приближения функции Q(x)
14. Вероятность ошибки для различных систем двоичных сигналов в канале с аддитивным белым гауссовским шумом
Ранее получено, что вероятность ошибки для двоичных сигналов может быть найдена как
& |
|
# |
, |
Pe ( Q |
|
! |
|
|
2N0 |
! |
|
% |
|
|
где - расстояние между сигналами, N0 / 2 - значение спектральной плотности мощности АБГШ. Рассмотрим три различных набора двоичных сигналов.
1. Противоположные сигналы. Пусть )1 (t) некоторая нормированная функция, заданная на интервале [0,T ] и определяющая форму сигнала, 
 )1
)1 
 ( 1.
( 1.
Положим что s0 (t) (  E)1 (t) , s1 (t) (
E)1 (t) , s1 (t) (  E)1 (t) , где E энергия сигналов,
E)1 (t) , где E энергия сигналов,
T T
E ( + s02 (t)dt ( + s12 (t)dt .
0 0
Оба сигнала могут быть представлены с использованием всего одной базисной функции. Это значит, что противоположные сигналы образуют одномерное
сигнальное множество, s0 ( ( E ) , |
s1 ( ( |
E ) . Легко заметить, что решающие |
|||
области в данном случае имеют вид бесконечных полупрямых R0 ( [0, ,) , |
|||||
R1 ( (,,0) , см. рис.14.1 |
|
|
|
|
|
|
s1 |
|
|
s0 |
|
|
E |
|
|
|
|
|
0 |
E |
|||
Рис.14.1 Сигнальное множество (противоположные сигналы)
Очевидно, что расстояние между сигналами равно ( 2 E , тогда вероятность ошибки равна
E , тогда вероятность ошибки равна

|
& |
# |
(14.1) |
P(пр) ( Q |
2E ! . |
||
e |
|
! |
|
|
% |
N0 |
|
Величина E / N0 называется отношением сигнал/шум. В инженерной практике принято выражать это отношение в децибелах (дБ). Величина отношения, измеренная в дБ, определяется как
−E / N0 .дБ ( 10 log10 −E / N0 .,
и наоборот
E / N0 ( 10−E / N0 .дБ / 10 .
Перевод отношения в децибелы и обратно можно легко выполнять в уме, если запомнить несложные правила:
a) при увеличении отношения в два раза, соответствующая величина в децибелах увеличивается на 3 дБ (точнее на 3.01 дБ), так как 10 log10 2 ( 3.01 / 3 ;
б) при уменьшении отношения в два раза, соответствующая величина в
децибелах |
уменьшается |
на |
3 дБ |
(точнее |
на |
3.01 |
|
|
дБ) |
так |
как |
||||||||||||||
10 log10 (1/ 2) ( 3.01 / 3 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Пусть E / N0 ( 5 . Требуется оценить −E / N0 .дБ . Легко видеть, |
|||||||||||||||||||||||||
что −E / N0 .дБ ( 7 дБ , действительно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
10 log10 5 ( 10 log10 (10 / 2) ( 10 log10 10 10 log10 2 ( 10 3 ( 7 . □ |
|
|
|||||||||||||||||||||||
2. Ортогональные сигналы. Пусть )1 (t) и ) 2 (t) две ортонормированные |
|||||||||||||||||||||||||
функции, заданные на интервале [0,T ] , |
()1 ,) 2 ) ( 0 и |
|
|
|
)1 |
|
|
|
( |
|
|
|
) 2 |
|
|
|
( 1. Положим |
||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
что s0 (t) ( |
E)1 (t) , s1 (t) ( |
E) 2 (t) , где |
E - |
энергия сигналов. В этом случае |
|||||||||||||||||||||
+0T s0 (t)s1 (t)dt ( 0 , и сигналы имеют равную энергию |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
T |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E ( + s02 (t)dt ( + s12 (t)dt . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сигналы могут быть представлены с использованием двух базисных |
|||||||||||||||||||||||||
функций. Это значит, что ортогональные |
сигналы образуют |
двумерное |
|||||||||||||||||||||||
сигнальное |
множество, |
s0 ( ( |
E ,0) , |
s1 ( (0, |
E ) . |
|
Легко |
|
заметить, |
что |
|||||||||||||||

решающие области в данном случае имеют вид бесконечных полуплоскостей
R0 ( {r ( (r1 , r2 ) : r1 0 r2 } , R1 ( {r ( (r1 , r2 ) : r1 1 r2 } , см. рис.14.2 .
Очевидно, что расстояние между сигналами равно (  2E , тогда
2E , тогда
E  s1
s1
s0
0
 E
E
Рис.14.2 Сигнальное множество (ортогональные сигналы)
вероятность ошибки равна
P |
(орт) |
& |
E |
# |
(14.2) |
|
( Q |
|
! . |
||
e |
|
N0 |
! |
|
|
|
|
% |
|
|
|
□
3. Сигналы с пассивной паузой. В этом случае s0 (t) ( 0 , s1 (t) 2 0 и
T
E ( +0 s12 (t)dt . Базис для представления этого набора сигналов состоит из одной функции)1 (t) ( s1 (t) /  E . Тогда s1 (t) (
E . Тогда s1 (t) (  E)1 (t) и
E)1 (t) и 
 )1
)1 
 ( 1. Сигналы с пассивной паузой образуют одномерное сигнальное множество, s0 ( (0) , s1 ( (
( 1. Сигналы с пассивной паузой образуют одномерное сигнальное множество, s0 ( (0) , s1 ( ( E ) . Легко заметить, что решающие области в данном случае имеют вид бесконечных полупрямых R0 ( (,,
E ) . Легко заметить, что решающие области в данном случае имеют вид бесконечных полупрямых R0 ( (,,  E / 2) , R1 ( (
E / 2) , R1 ( ( E / 2, ,) , см. рис.14.3
E / 2, ,) , см. рис.14.3
s0 |
s1 |
0 |
E |
Рис.14.3 Сигнальное множество (сигналы с пассивной паузой)
Очевидно, что расстояние между сигналами равно (  E , тогда вероятность ошибки равна
E , тогда вероятность ошибки равна
|
& |
E |
# |
(14.3) |
P(пп) ( Q |
! . |
|||
e |
|
2N0 |
! |
|
|
% |
|
|
|
□
Pe
E / N0 , дБ
Рис.14.1 Вероятность ошибки для двоичных сигналов
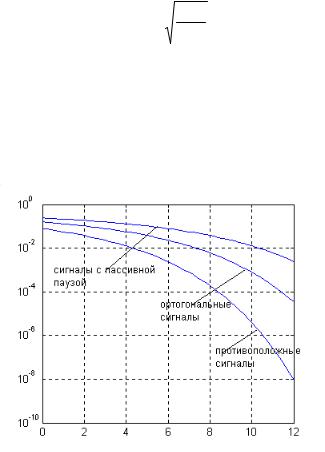
Приведенные выражения для вероятности ошибки справедливы при любой форме сигналов (при сохранении противоположности или ортогональности). От формы сигналов зависят другие свойства сигналов, в частности, спектральные свойства.
Как видно из равенств (14.1)-(14.3) и графиков, представленных на рис.14.1, наименьшую вероятность ошибки обеспечивают противоположные сигналы. При использовании ортогональных сигналов для достижения той же вероятности ошибки требуется вдвое (или на 3дБ) большее отношение сигнал/шум, чем при использовании противоположных сигналов. Сигналы с пассивной паузой уступают ортогональным 3дБ, а противоположным - 6 дБ.
15. Дискретная амплитудная модуляция. Вероятность ошибки
Сигналы дискретной амплитудной модуляции (АМ) |
имеют |
вид |
si (t) = Aiϕ(t) , где ϕi (t) - некоторая нормированная функция, |
заданная |
на |
интервале [0,T ] и определяющая форму сигнала, Ai - амплитуда i -го сигнала, i = 0,1,...q −1. Определим амплитуду i -го сигнала как
|
|
A = |
E |
|
|
2i |
|
|
|
||
|
|
1 − |
. |
|
|
||||||
|
|
|
i |
|
|
|
q −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда A0 = |
E , |
Aq−1 = − E , |
а |
все |
|
|
промежуточные |
значения |
амплитуды |
||
расположены |
с |
равномерным |
шагом |
|
|
в |
интервале [− |
E , E ] . |
Сигнальное |
||
множество АМ показано на рис 15.1. |
|
|
|
|
|
|
|
||||
|
|
sq−1 |
|
|
|
|
s1 |
s0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
E |
|
0 |
|
|
E |
|
|
|
Рис.15.1 Сигнальное множество АМ сигналов.
Минимальное расстояние между сигналами, как видно из рис.15.1, составляет
∆ = 2 E /(q −1) . Определим энергию каждого сигнала. Очевидно, что энергия i -го сигнала равна
E /(q −1) . Определим энергию каждого сигнала. Очевидно, что энергия i -го сигнала равна
Ei = Ai 2 = E 1 − q2−i1 2 ,
то есть энергия сигналов принимает различные значения. Величина E имеет смысл максимальной энергии. Как обычно будем полагать, что сигналы передаются равновероятно. Найдем значение средней энергии
|
|
q−1 |
|
E |
q−1 |
|
2i |
2 |
|
E |
q−1 |
|
4 |
q−1 |
|
4 |
|
q−1 |
|
||
E |
= |
∑ |
E P = |
1 |
− |
|
= |
|
∑ |
1 − |
∑ |
i + |
|
∑ |
i2 . |
||||||
|
|
|
|
|
|
2 |
|||||||||||||||
|
|
i i |
q |
∑ |
|
q −1 |
|
|
q |
|
|
(q −1) |
|
(q −1) |
|
||||||
|
|
i=0 |
|
i=0 |
|
|
|
i=0 |
|
i=0 |
|
|
i=0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
q−1 |
|
2i |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Найдем |
значение |
|
выражения |
|
|
|
|
|
|
|
|
|
1 |
− |
|
|
. |
Используя |
|
тождества |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q i=0 |
|
q −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∑ik=0 i = k(k +1) / 2 и ∑ik=0 i2 |
= k(k +1)(2k +1) / 6 , получим |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
1 |
|
q−1 |
|
2i |
|
|
2 |
1 |
q−1 |
|
|
|
|
4 |
|
q−1 |
|
|
4 |
|
|
|
q−1 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
∑ |
1 |
− |
|
|
= |
|
∑ |
1 − |
|
∑ |
i + |
|
|
|
∑ |
i |
2 = |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
q −1 |
|
|
q |
|
|
|
|
|
(q −1) |
|
|
(q −1) |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
q i=0 |
|
|
|
|
i=0 |
|
|
|
|
i=0 |
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
1 |
|
|
4 |
|
|
q(q −1) |
|
|
|
|
|
4 |
|
|
|
|
(q |
−1)q(2q −1) |
|
|
1 q +1 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
= |
|
|
|
q − |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
. |
|
|
|
|||
|
|
q |
(q −1) |
|
2 |
|
|
|
(q |
−1) |
2 |
|
|
|
6 |
|
|
3 q −1 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
E q +1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
(15.1) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 q −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решающие области |
для |
|
|
i =1,2,..., q − 2 |
представляют собой |
отрезки |
||||||||||||||||||||||||||||||||||||||
длины |
∆ с |
центрами |
|
в |
|
|
сигнальных |
точках |
s1 ,s2 ,...,sq−2 , |
то |
есть |
|||||||||||||||||||||||||||||||||
Ri = [ Ai |
− ∆/ 2, Ai + ∆/ 2) . |
Решающие |
области для |
крайних |
|
|
точек |
s0 |
и |
sq−1 |
||||||||||||||||||||||||||||||||||
представляют |
собой бесконечные |
|
|
|
|
полупрямые |
|
R0 =[ A0 − ∆/ 2, ∞) |
и |
|||||||||||||||||||||||||||||||||||
Rq−1 = (−∞, Aq−1 + ∆/ 2) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Сигнал на выходе канала имеет вид |
r(t) = s(t) + n(t) , |
|
где s(t) {si (t)} , |
|||||||||||||||||||||||||||||||||||||||||
n(t) – АБГШ со спектральной плотностью мощности |
N0 / 2 . В силу того, что |
|||||||||||||||||||||||||||||||||||||||||||
сигнальное множество АМ сигналов одномерно, имеем следующее
конечномерное представление r = A + n , где |
A {Ai }, |
n – г.с.в с параметрами |
|||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
= 0 , |
|
n2 |
= N0 / 2 . |
Найдем вероятность |
ошибки. |
По формуле полной |
|||
|
n |
||||||||||
вероятности имеем |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
q−1 |
|
1 |
q−1 |
|
|
|
|
|
|
|
|
Pe = ∑Pe (i)Pi |
= |
∑Pe (i) , |
(15.2) |
||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
i=0 |
|
q i=0 |
|
|
|
где Pe (i) - вероятность при передаче i -го сигнала, |
Pi |
- вероятность передачи |
|||||||||
i -го |
сигнала, Pi |
=1/ q . Рассмотрим |
сначала |
вычисление Pe (i) при |
|||||||
i =1,2,..., q − 2 .
Pe (i) = Pr[r Ri |
| i] = Pr[Ai |
+ n [ Ai − ∆/ 2, Ai |
+ ∆/ 2)]= Pr[n [−∆/ 2,+∆ |
|||||||||||||||||
−∆ / 2 |
1 |
|
2 |
/ |
N0 |
|
∞ |
|
1 |
|
|
|
2 |
/ N0 |
|
|
∆ |
|
||
= ∫ |
e |
−x |
dx + |
∫ |
|
|
e |
−x |
|
dx = |
|
|
||||||||
|
|
|
|
|
πN0 |
|
|
|
2Q |
2N0 |
. |
|||||||||
−∞ |
πN0 |
|
|
|
|
∆/ 2 |
|
|
|
|
|
|
|
|
||||||
Найдем оставшиеся вероятности Pe (0) и Pe (q −1) |
|
|
|
|
||||||||||||||||
Pe (0) = Pr[r R0 |
| 0] = Pr[A0 |
+ n [ A0 − ∆/ 2, ∞)]= Pr[n [−∆/ 2, ∞)] |
||||||||||||||||||
|
|
−∆ / 2 |
|
1 |
|
|
2 |
/ N0 |
|
|
|
|
|
|
∆ |
|
|
|
||
|
|
= ∫ |
|
|
e |
−x |
dx |
|
|
|
|
|
|
|
||||||
|
|
|
|
πN0 |
|
|
|
= Q |
2N0 |
. |
|
|
||||||||
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Аналогично можно показать, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
P (q −1) = Q |
|
|
|
|
. |
|
|
|
|
|
|
|||||||
|
|
|
e |
|
|
|
|
|
|
2N0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
/ 2)]=
(15.3)
=
(15.4)
(15.5)
Подстановка (15.3)-(15.5) в (15.2) с учетом того, что ∆ = 2 E /(q −1) дает окончательное выражение
E /(q −1) дает окончательное выражение
P |
= |
2q − 2 |
|
2E |
1 |
|
, |
(15.6) |
|
Q |
|
|
|
||||
e |
q |
|
N0 |
q −1 |
|
|
|
|
|
|
|
|
|
|
|||
определяющее зависимость вероятности ошибки от максимального отношения сигнал/шум E / N0 . С использованием равенства (15.1) получим выражение,
определяющее зависимость вероятности ошибки от среднего значения отношения сигнал/шум E / N0
P |
= |
|
|
6E |
1 |
|
(15.7) |
|
2q − 2 Q |
. |
|||||||
e |
|
q |
|
N |
|
q2 −1 |
|
|
|
|
|
|
|
0 |
|
|
|
При q = 2 равенства (15.6) и |
(15.7) обращаются в |
Pe = Q( 2E / N0 ) - |
||||||
вероятность ошибки для двоичных противоположных сигналов, при этом также
E = E .
Графики, показанные на рис. 15.2, дают представление о зависимости вероятности ошибки от среднего значения отношения сигнал/шум. Важно отметить, что вероятность ошибки резко возрастает с увеличением объема сигнального алфавита.
Pe
E / N0 , дБ
Рис.15.2 Вероятность ошибки для АМ сигналов
Рассмотрим вывод выражения для вероятности ошибки на бит для сигналов АМ. Среднее значения отношения сигнал шум/шум на бит равно
|
|
|
|
|
|
1 |
|
|
|
|
|
|
E |
|
E |
|
|||||||
|
|
|
|
|
= |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||
|
N0 |
|
|
log2 q N0 |
|
||||||
|
bit |
|
|
||||||||
Вероятность ошибки на бит зависит от отображения сообщений (номеров сигналов) в сигнальные точки. Предпочтительным будет такое отображение, при котором близко расположенные сигнальные точки соответствуют сообщениям, различающимся в малом числе двоичных разрядов. Такое отображение для сигналов АМ достигается с использованием кода Грея. В этом случае блоки двоичных данных, соответствующие соседним сигнальным точкам, будут отличаться только в одной позиции (см. пример для АМ-8 на Рис.15.3).
100 101 111 110 010 011 001 000
0
Рис.15.3 Сигнальное множество АМ –8 сигналов (отображение в соответствии с кодом Грея)
Поскольку ошибочное решение относительно переданного сигнала наиболее вероятно в пользу соседних сигналов, то оно будет приводить к ошибке только в одном бите. Это значит, что в большинстве случаев доля ошибочных двоичных разрядов при ошибочном решении равна 1/ log 2 q =1/ m . Отсюда следует, вероятность ошибки на бит как функции от отношения сигнал/шум на бит задается выражением
|
|
1 |
|
|
|
1 |
2q −2 |
|
|
|
E |
|
log2 q |
|
|
|
||
P |
≈ |
|
P |
= |
Q |
|
|
|
|
. |
(15.8) |
|||||||
|
|
|
|
|
6 |
|
|
|
2 |
|
|
|||||||
b |
|
log2 |
q |
e |
|
log2 q |
q |
|
|
N0 |
q |
−1 |
|
|
||||
|
|
|
|
|
|
|
bit |
|
|
|
|
|||||||

16. Квадратурная амплитудная модуляция. Вероятность ошибки
Сигналы квадратурной амплитудной модуляции (КАМ) (quadrature amplitude modulation, QAM) имеют вид si (t) = si1ϕ1 (t) + si2ϕ2 (t) , где ϕ1 (t), ϕ2 (t) - две ортонормированные функции, заданные на интервале [0,T ] и
определяющие форму сигнала, i = 0,1,..., q −1. Из определения сигналов КАМ следует, что D = 2 . Величины si1 , si2 для сигналов КАМ принимают дискретные значения равномерно расположенные в некотором конечном интервале. Они могут рассматриваться как амплитудные множители при функциях ϕ1 (t) и ϕ2 (t) , поэтому сигнал КАМ представляет собой сумму двух ортогональных АМ сигналов si1ϕ1 (t) и si2ϕ2 (t) .
Как обычно будем считать, что q = 2m , где m - целое; число m может
рассматриваться как число бит переносимых сигналом (при отсутствии
кодирования). Положим для начала, что m = 2k , k - целое. Тогда |
q = 2k |
тоже |
||||||||||||||||
целое. Поставим в соответствие номеру сигнала i , |
i = 0,1,..., q −1, пару целых i1 |
|||||||||||||||||
и i2 , i1 ,i2 = 0,1,..., q −1, по правилу i = i1 |
q + i2 . Иначе говоря, i1 , |
i2 это цифры |
||||||||||||||||
в |
|
|
-ичном представлении числа i . Положим, что |
|
|
|
|
|
|
|
||||||||
q |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2i |
|
|
|
2i |
2 |
|
|
|
|
|||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
si1 = A 1 − |
q −1 |
, |
si2 = A 1 − |
q −1 |
, |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где A - максимальное абсолютное значение величин si1 |
и si2 . Очевидно, что |
|||||||||||||||||
значения величин si1 и si2 расположены с |
равномерным |
шагом |
в |
|||||||||||||||
интервале[−A, A] . Сигнальное множество КАМ показано на рис 16.1 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
б |
в |
Рис.16.1 Сигнальное множество КАМ а) q = 4 , б) q =16 , в) q = 64

При q = 2m , где m = 2k −1, сигнальное множество строится путем
“прореживания ” сигнального множества для q = 22k . Примеры приведены на рис.16.2 – множество для КАМ8 построено из множества КАМ16, а множество для КАМ32 из множества для КАМ64 путем выбрасывания половины точек.
а |
б |
Рис.16.2 Сигнальное множество КАМ а) q = 8 , б) q = 32
Минимальное расстояние между сигналами, как видно из рис.16.1, составляет
|
|
|
|
∆ = 2A /( |
q −1) . |
|
|
|
|
|
(16.1) |
|||
Определим энергию каждого сигнала. Очевидно, что энергия i -го |
||||||||||||||
сигнала равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
= s2 |
+ s2 |
|
− |
2i |
|
2 |
|
− |
2i |
|
|
2 |
i |
= A2 1 |
1 |
|
+ A2 |
1 |
|
2 |
|
, |
|||||
|
i1 |
i2 |
|
|
q −1 |
|
|
|
|
q −1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
то есть энергия сигналов принимает различные значения. Как обычно будем полагать, что сигналы передаются равновероятно. Найдем значение средней энергии
|
|
|
|
|
|
|
|
|
1 q−1 |
|
A2 |
q −1 q −1 |
|
|
|
2i |
|
2 |
|
|
|
2i |
2 |
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
E |
= |
|
∑Ei = |
|
|
|
|
|
|
|
|
|
− |
|
1 |
|
|
|
− |
|
|
|
|
|
|
= |
|
|
||||
|
|
|
|
|
|
q |
q |
∑ ∑ |
1 |
|
|
|
|
+ 1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
= |
0 |
|
i1 |
= |
0 i2 |
= |
|
|
|
|
q −1 |
|
|
|
q −1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
A |
2 |
q −1 |
|
|
|
|
2i |
|
2 |
|
q −1 |
|
|
|
|
2i |
|
|
2 |
2A |
2 q −1 |
|
2i |
|
2 |
||||||||||||
|
|
|
∑ |
|
|
|
+ ∑ |
|
|
|
2 |
|
|
∑ |
|
|
|
|||||||||||||||||||||
= |
|
|
|
|
|
|
1 |
|
|
|
|
− |
|
|
|
|
|
|
− |
1 |
|
|
||||||||||||||||
q |
|
q 1 − |
|
|
|
q 1 |
|
|
|
= |
|
|
|
1 |
|
. |
||||||||||||||||||||||
|
|
|
= |
0 |
|
|
|
|
q −1 |
|
|
i2 |
= |
0 |
|
|
|
|
q −1 |
|
|
q |
i1 |
= |
0 |
|
|
q −1 |
|
|||||||||
|
|
|
i1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
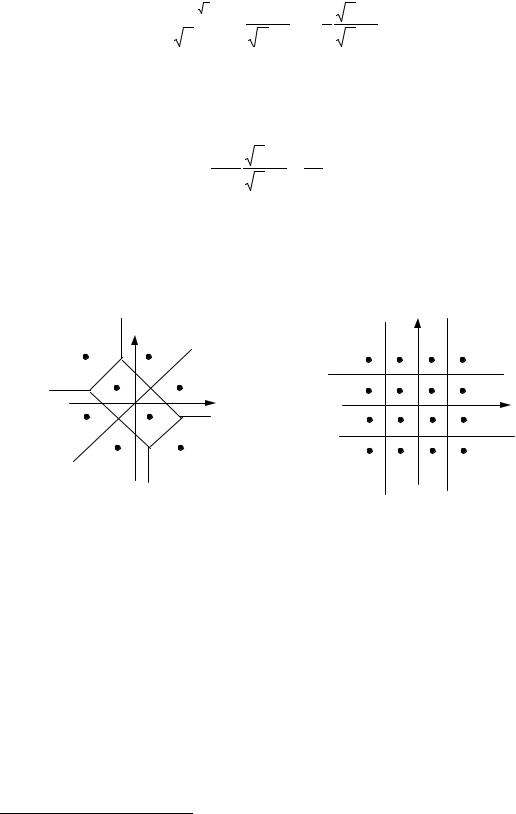
|
1 |
q−1 |
|
|
|
2i |
|
2 |
|
1 q |
+1 |
|
|
|
|
|||||
|
∑ |
|
|
|
|
|
|
|
|
|
||||||||||
Ранее получено, что |
|
|
|
1 |
− |
|
|
= |
|
|
|
|
|
|
. Отсюда легко следует, что |
|||||
|
|
|
q −1 |
3 q −1 |
||||||||||||||||
|
q i=0 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
1 |
|
|
q −1 |
|
|
2i |
2 |
|
|
|
1 |
q +1 |
|
|||
|
|
|
|
|
|
|
|
− |
|
1 |
|
|
|
= |
|
|
. |
|||
|
|
|
|
q |
|
∑ 1 |
q |
−1 |
|
3 |
q −1 |
|||||||||
|
|
|
|
|
i1 =0 |
|
|
|
|
|
|
|
||||||||
Тогда с учетом (16.1) имеем соотношение между средней энергией сигналов КАМ и минимальным расстоянием между ними
|
= |
2A2 |
q +1 |
= |
∆2 |
(q −1) |
(16.2) |
E |
|||||||
|
|
3 |
q −1 |
|
6 |
|
|
Решающие области для сигнальных точек, находящихся в середине сигнального созвездия, представляют собой квадраты. Для точек на краях сигнального созвездия они бесконечны (см. рис.16.3).
а |
б |
Рис.16.3 Решающие области КАМ а) q = 8 , б) q =16
Оценим вероятность ошибки для КАМ сигналов1. Вероятность ошибки вычисляется как
q−1 |
1 |
q−1 |
|
Pe = ∑Pe (i)Pi = |
∑Pe (i) , |
(16.3) |
|
i=0 |
q i=0 |
|
|
1 Вывод точного выражения для вероятности ошибки приведен в Приложении 3.

где Pe (i) вероятность ошибки при передаче i -го сигнала, Pi вероятность
передачи i -го сигнала, |
Pi =1/ q . |
Рассмотрим вычисление |
Pe (i) . По |
|
определению Pe (i) = Pr[r Ri | i] , где Ri - i -ая решающая область, |
r = si + n - |
|||
точка в сигнальном пространстве, соответствующая принятому сигналу. |
||||
Обозначим квадрат с длиной стороны |
∆и центром в некоторой точке |
|||
z = (z1 , z2 ) как S(z) . Он может быть описан как |
|
|
||
S(z) = [z1 − ∆/ 2, z1 + ∆/ 2]×[z2 − ∆/ 2, z2 + ∆/ 2] . |
|
|||
Тогда S(si ) это квадрат с |
центром |
в i -й |
сигнальной точке и |
S(si ) Ri . |
Поэтому |
|
|
|
|
Pe (i) = Pr[r Ri | i] ≤ Pr[r S(si ) | i]= Pr[si |
+ n S(si )]= Pr[n S(0)]= |
|||
=1 − Pr[n S(0)]=1 − Pr[(n1 , n2 ) [−∆/ 2,+∆/ 2]×[−∆/ 2,+∆/ 2]]=
=1 − Pr[n1 [−∆/ 2,+∆/ 2]]Pr[n2 [−∆/ 2,+∆/ 2]]=
=1 |
|
∆ / 2 |
1 |
|
e−x |
2 |
|
2 |
|
|
|
|
∆ |
2 |
(16.4) |
− |
∫ |
|
|
/ N0 dx |
=1 − 1 |
− 2Q |
. |
||||||||
|
|
|
πN |
0 |
|
|
|
|
|
|
|
|
2N |
|
|
|
−∆ / 2 |
|
|
|
|
|
|
|
|
|
|
0 |
|
||
Подстановка (16.4) в (16.3) дает с учетом (16.2) оценку |
|
|
|
||||||||||||
|
|
|
P ≤ |
|
|
|
3E |
1 |
2 |
|
|
(16.5) |
|||
|
|
|
1 − 1 − 2Q |
. |
|
|
|||||||||
|
|
|
e |
|
|
|
|
N0 q −1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим получение более |
простой, |
|
но менее |
точной |
чем (16.5) |
||||||||||
оценки вероятности ошибки при использовании КАМ сигналов. Пусть C(z)
круг радиуса ∆/ 2 |
с центром z . Заметим что Ri S(si ) C(si ) , тогда |
|
|||||||||||||
|
|
Pe (i) ≤ Pr[n S(0)]< Pr[n C(0)] = Pr[n12 + n22 |
> (∆/ 2)2 ]. |
|
|||||||||||
Далее |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pr[n12 + n22 |
> (∆/ 2)2 ]= |
∫∫ |
|
|
1 |
|
e−x2 / N0 |
|
1 |
e−y 2 / N0 dxdy = |
|
||
|
|
|
|
|
|
x2 + y 2 >(∆ / 2)2 |
|
πN0 |
|
|
πN0 |
|
|
||
|
|
|
|
|
|
|
Переходкполярнымкоординатам: |
|
|||||||
|
|
|
|
|
|
|
|
||||||||
|
∫∫ |
(πN0 ) |
2 |
2 |
|
|
x = ρcosθ, y = ρsinθ |
|
|||||||
= |
−1e−( x |
+ y |
) / N0 dxdy = |
{x |
2 |
+ y |
2 |
> (∆/ 2) |
2 |
}= {ρ > ∆/ 2, 0 <θ < 2π} |
= |
||||
|
x2 + y 2 >(∆ / 2)2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
dxdy = ρdρdθ |
|
|
|
|
||||

= 2π ∞ (πN0 )−1 ρe−ρ2 / N0 dρdθ = |
∞ |
2ρ |
e−ρ2 / N0 dρ = − e−ρ2 / N0 |
|
∞ = e−∆2 / 4 N0 . |
||||||||||||
|
|||||||||||||||||
|
|
|
|
||||||||||||||
∫ ∫ |
|
|
|
∫ |
|
N0 |
|
|
|
|
|
|
|
∆ / 2 |
|||
0 ∆ / 2 |
|
|
∆ / 2 |
|
|
|
|
|
|
|
|
|
|||||
Следовательно |
P (i) < exp(−∆2 |
/ 4N |
0 |
) . Отсюда с использованием (16.2) и (16.3) |
|||||||||||||
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
получаем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
E |
|
|
|
||||||
|
P |
< exp |
|
− |
|
|
|
. |
(16.6) |
||||||||
|
|
|
|
|
|
||||||||||||
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2(q −1) N0 |
|
|
|
|||||||
На рис. 16.4 показаны графики границ вероятности ошибки, вычисленных по формулам (16.5) (сплошная линия ) и (16.6) ( пунктир) для q = 4,16,64 .
Pe
E / N0 , дБ
Рис.16.4 Границы вероятности ошибки для сигналов КАМ
Рассмотрим вывод выражения для вероятности ошибки на бит для сигналов КАМ. Среднее значения отношения сигнал шум/шум на бит равно
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
E |
|
E |
|
|
|||||||
|
|
|
|
|
= |
|
|
|
|
|
. |
(16.7) |
|
|
|
|
|
|
|
|
|||||
|
N0 |
|
|
log2 q N0 |
|
|
||||||
|
bit |
|
|
|
||||||||
Для отображения сообщений в сигнальные точки КАМ может использоваться код Грея. Для нумерации строк и столбцов в сигнальном созвездии

применяются два кода Грея длины m / 2 , m = log2 q . Сообщение, строится как конкатенация слов кода Грея для номеров строки и столбца, соответствующих сигнальной точке. Пример для КАМ-16 показан на рис. 16.5.
1010 |
1110 |
0110 |
0010 |
1011 |
1111 |
0111 |
0011 |
1001 |
1101 |
0101 |
0001 |
1000 |
1100 |
0100 |
0000 |
Рис.16.5 Сигнальное множество КАМ –16 (отображение в соответствии с кодом Грея для строк и столбцов)
Очевидно, что в этом случае соседним точкам соответствуют сообщения, отличающиеся в одном двоичном разряде. Поэтому формула для вероятности ошибки на бит может быть получена из выражений (16.5) и (16.7) как
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
1 |
|
|
|
E |
|
|
|
|||||
Pb ≈ |
|
Pe ≈ |
1− |
|
1 |
−2Q |
|
|
|
log2 q |
|
. |
||||
log2 |
q |
log2 |
|
|
3 |
N0 |
|
q −1 |
|
|
||||||
|
|
q |
|
|
|
bit |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17. Фазовая модуляция. Вероятность ошибки
Сигналы фазовой модуляции (ФМ) (phase shift keying, PSK) имеют вид
|
|
|
|
si (t) = |
2E / T cos(2πf0t −θi ), |
0 < t < T , |
|
|
|
|
(17.1) |
|||||||||||
где |
E энергия сигнала, |
T |
период следования сигналов, f0 |
несущая частота, |
||||||||||||||||||
f0 = l / T , |
l - целое, |
θi - |
|
фаза i -го |
|
сигнала, |
|
θi = i(2π / q) , |
i = 0,1,..., q −1. |
|||||||||||||
Равенство (17.1) можно переписать в виде |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
s |
(t) = |
E cosθ |
|
2 |
cos 2πf |
|
t + |
E sinθ |
|
2 sin 2πf |
|
t = s |
ϕ |
(t) + s |
|
ϕ |
|
(t) , (17.2) |
||||
i |
|
|
i |
T |
|
|
0 |
|
|
i |
T |
|
0 |
|
|
i1 1 |
|
|
i2 |
|
2 |
|
где |
si1 = |
E cosθi , |
si2 = |
|
E sinθi - |
коэффициенты |
разложения по |
|||||||||||||||
ортонормированным функциям |
ϕ1 (t) = |
|
2 / T cos 2πf0t |
и ϕ2 (t) = |
|
2 / T sin 2πf0t . |
||||||||||||||||
Из равенства (17.2) |
следует, что D = 2 |
в случае сигналов ФМ. Сигнальное |
||||||||||||||||||||
множество ФМ показано на рис 17.1 Сигнальные точки равномерно
расположены на окружности радиуса |
E , угол между радиусами, |
|
соединяющими соседние сигнальные точки равен |
2π / q . Следовательно, |
|
минимальное расстояние между сигналами равно ∆ = 2 |
E sin(π / q) . |
|
si
s1
θi
s0
sk |
sq−1 |
Rk
Рис.17.1 Сигнальное множество ФМ
Решающая область Rk для k -го |
ФМ |
сигнала представляют собой угол |
||||
величины 2π / q |
с вершиной в |
начале |
координат, биссектриса |
которого |
||
проходит через точку sk (см. рис. 17.1). |
|
|
||||
Оценим |
вероятность ошибки для ФМ сигналов. Вероятность ошибки |
|||||
вычисляется как |
|
|
|
|
|
|
|
q−1 |
|
1 |
|
q−1 |
|
|
Pe = ∑Pe (i)Pi = |
|
∑Pe (i) , |
(17.3) |
||
|
|
|||||
|
i=0 |
|
q i=0 |
|
||
где Pe (i) вероятность ошибки при передаче i -го сигнала, Pi вероятность
передачи i -го сигнала, Pi =1/ q . Рассмотрим вычисление |
Pe (i) . По |
определению Pe (i) = Pr[r Ri | i] , где Ri - i -ая решающая область, |
r = si +n - |
точка в сигнальном пространстве, соответствующая принятому сигналу. Рассмотрим рис.17.2
l2 |
si |
l1 |
si+1 |
|
si−1 |
Ri
Рис.17.2. К вычислению вероятности ошибки для ФМ
Нетрудно заметить, что
Pe (i) = Pr[r Ri | i] = Pr[r лежитправеепрямойl1 или r лежит левеепрямойl2 | i] <
<Pr[r лежит правее прямой l1 | i] + Pr[r лежит левее прямой l2 | i] =
=Pr[d(r, si−1 ) < d(r, si ) | i] + Pr[d(r, si+1 ) < d(r,si ) | i] =
|
∆ |
|
|
∆ |
|
|
2E |
sin |
π |
(17.4) |
= Q |
|
|
+ Q |
|
|
= 2Q |
|
. |
||
|
2N0 |
|
|
|
|
|
N0 |
|
|
|
|
|
|
2N0 |
|
|
q |
|
|||
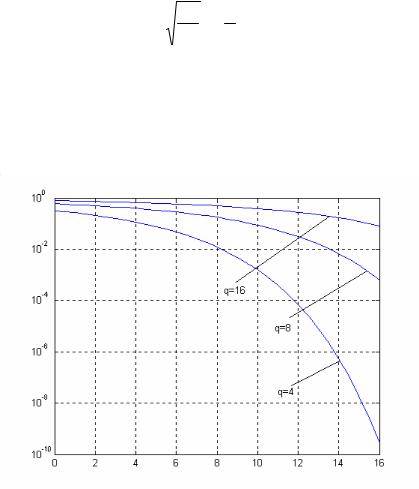
При переходе от первой ко второй строке (17.4) использовано аддитивное неравенство. Далее использовано общее выражение для вероятности ошибочного приема в системе передачи с двоичными сигналами и выражение для минимального расстояния сигналов ФМ. В итоге после подстановки (17.4) в (17.3) получаем, что
|
|
2E |
sin |
π |
(17.5) |
P < 2Q |
N0 |
. |
|||
e |
|
|
q |
|
|
|
|
|
|
|
|
На рис. 17.3 показаны графики границы вероятности ошибки, вычисленной по формуле (17.5).
Pe
E / N0 , дБ
Рис.17.3 Граница вероятности ошибки для сигналов ФМ
Для сигналов ФМ номера сигналов обычно отображаются в сигнальные точки с использованием кода Грея. В этом случае блоки двоичных данных, соответствующие соседним сигнальным точкам, отличаются только в одной позиции (см. пример для ФМ-8 на Рис.17.4).
011
010
001
110 |
000 |
111 |
100 |
|
|
|
101 |
Рис.17.4 Сигнальное множество ФМ-8 (отображение в соответствии с кодом Грея)
Поскольку ошибочное решение относительно переданного сигнала наиболее вероятно в пользу соседних сигналов, то оно будет приводить к ошибке только в одном бите. Это значит, что доля ошибочных двоичных разрядов при ошибочном решении равна 1/ log 2 q =1/ m . Отсюда следует, что вероятность ошибки на бит как функция от отношения сигнал/шум на бит задается выражением
|
1 |
|
2 |
|
|
|
E |
|
|
|
|
Pb ≈ |
Pe < |
Q |
|
|
|
log2 q sin |
π |
. |
|||
|
|
|
2 |
|
|
|
|||||
|
log2 q |
|
log2 q |
|
|
N0 |
|
|
|||
|
|
|
|
|
bit |
|
q |
|
18. Частотная модуляция. Вероятность ошибки
Сигналы частотной модуляции (ЧМ) (frequency shift keying, FSK) имеют
вид |
|
si (t) = 2E / T cos 2πfi t, 0 < t < T , |
(18.1) |
где E энергия сигнала, T период следования сигналов, fi центральная частота i -го сигнала, fi = li / T , li - целое, i = 0,1,..., q −1. Величины li должны быть различны при различных i . При таком выборе центральных частот сигналы ЧМ
будут ортогональными. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Естественно |
выбрать |
в |
|
качестве |
|
базиса |
функции |
вида |
|||||||||
ϕi (t) = 2 / T cos 2πfi t . Можно проверить, что |
|
|
|
|
|
|
|
|
|||||||||
(ϕi ,ϕk ) = |
sin 2π(l |
i |
+ l |
k |
) |
+ |
sin 2π(l |
i |
−l |
k |
) |
= |
1, i = k |
. |
|
||
|
|
|
|
|
|
|
|
|
|||||||||
2π(li + lk ) |
|
2π(li −lk ) |
|
|
|||||||||||||
|
|
|
|
|
|
0, i ≠ k |
|
|
|||||||||
Число базисных функций совпадает в этом случае с числом сигналов, то есть
D = q . Тогда можно записать, что si (t) =  Eϕi (t) , а сигнальные точки тогда будут иметь вид
Eϕi (t) , а сигнальные точки тогда будут иметь вид
s0 |
= ( |
E,0,0,...,0) |
s1 |
= (0, |
E,0,...,0) |
... |
|
|
sq−1 = (0,0,...,  E )
E )
Сигнальное созвездие может быть изображено только в случаях q = 2 и q = 3 .
Наглядное описание решающих |
областей также |
возможно только в этих |
случаях. |
|
|
Оценим вероятность ошибки для ЧМ сигналов. Вероятность ошибки |
||
вычисляется как |
|
|
q−1 |
q−1 |
|
Pe = ∑Pe (i)Pi = 1 ∑Pe (i) , |
(18.2) |
|
i=0 |
q i=0 |
|
где Pe (i) - вероятность |
ошибки при передаче i -го сигнала, Pi - вероятность |
|
передачи i -го сигнала, |
Pi =1/ q . Рассмотрим вычисление Pe (i) . |
Условная |
вероятность ошибки может быть записана как |
|
|
|
Pe (i) =1 − Pc (i) , |
(18.3) |
где Pc (i) вероятность правильного решения при передаче i -го сигнала. При оптимальном приеме в канале с АБГШ вероятность правильного приема определяется как
P (i) = Pr[d(r,s |
) = min d(r,s |
k |
) | i] = Pr[d 2 |
(r,s |
i |
) |
= min d 2 (r,s |
k |
) | i] . |
||||||||||||
c |
i |
0≤k <q |
|
|
|
|
|
|
|
|
|
|
|
|
0≤k <q |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Это равенство можно переписать в виде |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P (i) |
= Pr |
q−1 {d 2 (r,s |
) |
< d 2 (r,s |
k |
)}| i . |
|
|
|
|||||||||||
|
|
c |
|
I |
|
|
|
|
i |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k ≠i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку |
|
|
2 = r 2 − 2(r,s j ) + s j |
2 = r 2 − 2 Erj + E , |
|||||||||||||||||
d 2 (r,s j ) = r −s j |
|||||||||||||||||||||
для любого |
j = 0,1,..., q −1 , |
то |
условие |
d 2 (r,si ) < d 2 (r, s k ) |
эквивалентно |
||||||||||||||||
условию ri > rk . Поэтому можно записать, что |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
q−1 |
{r |
|
|
|
|
|
|
|
|
|
||
|
|
|
P (i) = |
Pr |
|
> r }| i . |
|
|
|
|
|
|
|||||||||
|
|
|
c |
|
|
|
|
|
I |
|
i |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k ≠i |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При передаче i -го сигнала ri = |
|
E + ni , |
rk = nk , |
гдеni |
nk , k = 0,1,..., q −1, k ≠ i , |
||||||||||||||||
независимые гауссовские с.в. с параметрами (0, N0 / 2) . Следовательно, |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Pc (i) = Pr Iq−1 { E + ni > nk } , |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
k |
≠i |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
или, переходя к нормированным переменным ηi |
= ni |
|
/ |
N0 / 2 , ηk |
= nk / N0 / 2 , |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pc (i) = Pr Iq−1 { 2E / N0 +ηi >ηk } . |
|
|
|
||||||||||||||||
|
|
|
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k ≠i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь ηi , ηk , |
k = 0,1,..., q −1, k ≠ i , независимые гауссовские с.в. с параметрами |
||||||||||||||||||||
(0,1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Для получения результата поступим следующим образом: 1)
зафиксируем значение |
z = 2E / N0 +ηi , 2) |
найдем значение вероятности |
||
Pr[ |
q−1 |
{z >ηk }], и 3) |
усредним по значению |
z = 2E / N0 +ηi . |
Ik =0,k ≠i |
|
|
|
|
q−1 |
|
∞ |
q−1 |
|
||
Pc (i) = Pr I{ |
2E / N0 +ηi >ηk } |
= ∫Pr I{z >ηk } |
||||
|
k =0 |
|
−∞ |
|
k =0 |
|
k ≠i |
|
k ≠i |
||||
|
|
|
|
|
|
|
Далее,
q−1 |
|
q−1 |
q−1 |
|
Pr I{z >ηk } |
= ∏Pr[z >ηk ] = ∏(1 −Q(z)) |
|||
|
k =0 |
|
k =0 |
k =0 |
|
k ≠i |
k ≠i |
||
k ≠i |
|
|||
1 |
e |
−( z− 2 E / N0 )2 / 2 |
dz . |
2π |
|
= (1 −Q(z))q−1.
(18.4)
(18.5)
Подстановка (18.5) в (18.4) и далее в (18.3) |
и в (18.2) дает в результате |
|
||||
∞ |
|
1 |
|
|
|
|
Pe =1 − ∫(1 −Q(z)) |
q−1 |
e |
−( z− 2 E / N0 )2 / 2 |
dz . |
(18.6) |
|
|
2π |
|
||||
−∞ |
|
|
|
|
|
|
Формула (18.6) дает точное значение вероятности ошибки, но его вычисление требует численного интегрирования. Для этой вероятности можно легко получить просто вычисляемую верхнюю границу. Ее вывод основан на использовании аддитивного неравенства. Условная вероятность ошибки может быть найдена как
|
|
|
{d 2 |
|
|
|
|
|
|
P (i) = Pr q−1 |
(r,s |
i |
) > d 2 |
(r,s |
k |
)}| i . |
|||
e |
U |
|
|
|
|
|
|||
|
|
k =0 |
|
|
|
|
|
|
|
|
k ≠i |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Применяя аддитивную границу, имеем
q−1
Pe (i) ≤ ∑Pr[d
k =0 k ≠i
q−1
= ∑Pr[
k =0 k ≠i
И окончательно,
q−1 |
q−1 |
2 (r,si ) > d 2 (r,sk ) | i] = ∑Pr[ri < rk | i] = ∑Pr[ E + ni < nk ] = |
|
k =0 |
k =0 |
k ≠i |
k ≠i |
 2E / N0 +ηi <ηk ] = ∑q−1 Q( E / N0 )= (q −1)Q(
2E / N0 +ηi <ηk ] = ∑q−1 Q( E / N0 )= (q −1)Q( E / N0 ).
E / N0 ).
k =0 k ≠i
Pe ≤ (q −1)Q( E / N0 ). |
(18.7) |

Граница (18.7) вычисляется гораздо проще, чем точное значение (18.6). Точность оценки (18.7) во многих случаях оказывается вполне приемлемой. Заметим также, что при q = 2 граница и точное значение совпадают. На рис. 18.1 показаны графики вероятности ошибки (сплошная линия) и оценки вероятности ошибки (пунктир) в зависимости от отношения сигнал/шум.
Pe
E / N0 , дБ
Рис.18.1 Вероятность ошибки и граница вероятности ошибки для сигналов ЧМ
Рассмотрим вывод выражения для вероятности ошибки на бит. Ранее было показано, что вероятность ошибки на бит может быть вычислена как
|
1 |
q−1 q−1 |
|
Pb = |
∑∑Pe (i,i')n(i,i')Pi , |
||
|
|||
|
m i=0 i'=0 |
||
|
|
i'≠i |
|
где Pe (i,i') - вероятность принятия решения в пользу сигнала с номером i' при условии, что был передан сигнал с номером i , i' ≠ i , n(i, i') число разрядов, в
которых различаются двоичные представления номеров сигналов i и i' . При использовании ортогональных сигналов и, в частности, сигналов ЧМ,
Pe (i, i') = Pe (i) /(q −1)
для всех i' ≠ i . Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
q−1 q−1 |
P (i) |
|
|
|
1 |
|
|
q−1 |
q−1 |
|
|||||
|
Pb |
= |
|
|
|
∑∑ |
|
e |
|
n(i,i')Pi = |
|
|
|
∑Pe (i)Pi ∑n(i,i') . |
(18.8) |
||||||
|
|
|
q −1 |
|
|
|
|||||||||||||||
|
|
|
|
m i=0 i'=0 |
|
|
|
m(q −1) i=0 |
i'=0 |
|
|||||||||||
|
|
|
|
|
|
i'≠i |
|
|
|
|
|
|
|
|
|
|
|
|
i'≠i |
|
|
|
|
|
|
|
|
q−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим сумму |
∑n(i,i') . |
Пусть |
j |
- число различий в двоичной записи |
|||||||||||||||||
|
|
|
|
|
|
i'=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i'≠i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
величин i и i' ; ясно, что 1 ≤ j ≤ m . Тогда легко заметить, что |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
q−1 |
|
m |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
∑n(i,i') = ∑ jCmj , |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
i'=0 |
|
j=1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
i'≠i |
|
|
|
|
|
|
|
|
|
|
и далее |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
m |
|
|
|
|
m! |
|
|
m |
|
|
m! |
|
|
m |
m(m −1)! |
|
|
|||
∑ jCmj =∑ j |
|
|
|
|
|
=∑ |
|
|
|
=∑ |
|
= |
|||||||||
|
j!(m − j)! |
|
|
|
|
|
|
|
|||||||||||||
j=1 |
j=1 |
|
|
j=1 ( j −1)!(m − j)! |
j=1 ( j −1)!((m −1) −( j −1))! |
|
|||||||||||||||
mm−1
=m∑Cmj−−11 = m∑Cml −1 = m2m−1 ,
j=1 l=0
то есть
q−1
∑n(i,i') = m2m−1 .
i'=0 i'≠i
Подставляя полученное выражение |
в (18.8) |
и принимая во внимание, что |
||||
q = 2m имеем для ортогональных сигналов |
|
|
||||
P = |
|
2m−1 |
|
P . |
|
|
|
2m −1 |
|
||||
b |
|
|
e |
|
||
Заметим, что для двоичных сигналов, то есть когда q = 2 и m =1, Pb |
= Pe , а при |
|||||
q >>1 Pb ≈ Pe / 2 . |
|
|
|
|
|
|
Отношение сигнал/шум на |
|
бит |
Eb / N0 = (1/ m)E / N0 , |
поэтому |
||
окончательное выражение для вероятности ошибки на бит, как следует из формулы (18.6), имеет вид
|
2m−1 |
∞ |
q−1 1 |
|
−( z− 2mEb / N0 )2 / 2 |
|
||||
Pb = |
|
|
|
|
|
− ∫(1 −Q(z)) |
|
e |
|
|
2 |
m |
−1 |
1 |
2π |
|
dz . |
||||
|
|
|
−∞ |
|
|
|
||||

19. Предельные характеристики достижимые при использовании ортогональных сигналов
Рассмотрим передачу с использованием ортогональных сигналов. Пусть
si (t) = Eϕi (t) , где ϕi (t) , i = 0,1,..., q −1, - |
ортонормированные |
функции, |
заданные на интервале [0,T ] , E -энергия |
сигнала. В качестве |
базисных |
функций могут рассматриваться, в частности, отрезки гармоник соответствующим образом выбранных различных частот. Получающиеся при этом сигналы соответствуют сигналам ЧМ.
Выражение для вероятности ошибки, полученное при рассмотрении ЧМ, справедливо для любых ортогональных сигналов и имеет вид
∞ |
|
1 |
|
|
|
|
|
|
Pe =1 − ∫(1 −Q(z)) |
q−1 |
|
e |
−( z− 2 E / N0 )2 / 2 |
dz |
(19.1) |
||
|
2π |
|
|
|||||
−∞ |
|
|
|
|
|
|
||
и, кроме того |
|
|
|
|
|
|
|
|
Pe ≤ (q −1)Q( |
E / N0 ). |
|
|
(19.2) |
||||
Рассмотрим передачу при различных значениях q . Число |
двоичных |
|||||||
единиц (бит), переносимых q -ичным сигналом, |
равно m = log2 q . |
При этом |
||||||
энергия, приходящаяся на один переданный бит, |
равна Eb = E / m ; |
определим |
||||||
также отношение сигнал/шум на бит Eb / N0 . Логично рассмотреть вероятность
ошибки на бит Pb в отличие от вероятности ошибки на символ (сигнал) Pe и
построить зависимость Pb от |
Eb / N0 при различных q . Ранее было показано, |
|||||||||||
что вероятность ошибки на бит может быть вычислена как |
|
|
||||||||||
|
|
|
|
|
|
2m−1 |
|
|
|
|
|
|
|
|
|
|
|
P = |
|
P . |
|
|
|
(19.3) |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
b |
2m −1 |
e |
|
|
|
|
|
Заметим, что для двоичных сигналов, то есть когда q = 2 и m =1, |
Pb = Pe , а при |
|||||||||||
q >>1 Pb ≈ Pe / 2 . Из (19.1) и (19.4) следует, что |
|
|
|
|
||||||||
|
2m−1 |
∞ |
|
|
q−1 1 |
|
−( z− 2mEb / N0 )2 / 2 |
|
|
|||
Pb = |
|
|
|
|
− ∫(1 |
−Q(z)) |
|
e |
|
|
|
|
2 |
m |
|
1 |
2π |
|
dz . |
||||||
|
|
−1 |
−∞ |
|
|
|
|
|
|
|||
На рис. 19.1 показаны графики вероятности ошибки на бит в зависимости от отношения сигнал/шум на бит.

Pb
Eb / N0 , дБ
Рис.19.1 Вероятность ошибки на бит для ортогональных сигналов
Как следует из рассмотрения графиков, вероятность ошибки на бит убывает с ростом числа сигналов, если отношение сигнал/шум на бит оказывается не слишком малым. Оценим величину этого порогового значения. Для этого,
основываясь на оценке (19.2), получим соответствующую оценку для Pb . Из
(19.2) и (19.3) следует, что
Pb ≤ 2m−1 Q( mEb / N0 ).
mEb / N0 ).
Используя оценку Q(x) < exp(−x2 / 2) / 2 , получим
P < 2m−2 |
exp(−(m / 2)E |
b |
/ N |
0 |
) = exp(− (m / 2)(E |
b |
/ N |
0 |
− 2 ln 2))/ 4 . (19.4) |
|
b |
|
|
|
|
|
|
||||
Последнее равенство |
означает, |
что если Eb / N0 |
> 2 ln 2 1 (что соответствует |
|||||||
только 1.41 дБ!), то вероятность ошибки может быть сделана сколь угодно малой при возрастании m . Из этого утверждения можно было бы сделать вывод о возможности построения сколь угодно надежного метода передачи с
использованием ортогональных сигналов. Например, если |
Eb / N0 |
= 2 дБ, |
то |
||
при |
m =50 из (19.4) следует, что P < 2 10−7 |
; если же |
взять |
m = 80 , |
то |
|
b |
|
|
|
|
1 На самом деле пороговое значение отношения сигнал/шум на бит равно не 2ln2 а ln2 (-1.59 дБ). Неточность в определении порогового значения связана с использованием сравнительно слабой границы вероятности ошибки.
Pb < 3 10 −11 . На практике такой метод оказывается нереализуемым. При увеличении m экспоненциально возрастает число ортогональных сигналов, т.к. q = 2m . В рассмотренных примерах число сигналов равно 1.1 1015 и 1.2 1024
соответственно. Это приводит к экспоненциальному возрастанию полосы частот, требуемой для передачи и экспоненциальному возрастанию сложности формирования и приема сигналов. Практически реализуемые методы передачи с использованием ортогональных сигналов основываются на применении сигналов из сравнительного небольшого алфавита и формировании из них длинных последовательностей (кодирования). При возрастании длины этих последовательностей можно добиться требуемой надежности передачи без неприемлемого расширения полосы частот и увеличения сложности обработки.

20. Сравнительная характеристика АМ, КАМ, ФМ и ЧМ.
|
|
Сигналы АМ имеют вид |
|
|
|
|
|||
|
|
|
|
|
|
si (t) Ai! (t) , |
|
|
|
где Ai |
E #1% 2i /(q % 1) , |
i 0,1,...q % 1, E - максимальная энергия сигналов. |
|||||||
|
|
Сигналы КАМ могут быть представлены в виде |
|
|
|||||
|
|
|
|
|
si (t) si1!1 (t) & si2! 2 (t) , |
|
|
||
где si1 |
A#1% 2i1 /( q % 1) , |
si 2 |
A#1% 2i2 /( q % 1) , i1 , i2 0,1,..., |
q % 1. |
|
||||
|
|
Сигналы ФМ имеют вид |
|
|
|
|
|||
|
|
|
ФМ: si (t) |
2E / T cos(2 f0t % 2 i / q) , |
|
|
|||
где i 0,1,...q % 1, |
E - энергия сигналов. И, наконец, выражение для ЧМ сигналов |
||||||||
|
|
|
|
|
si (t) |
2E / T cos 2 fi t , |
|
|
|
где E |
энергия |
сигнала, |
fi |
несущая (центральная) частота |
i -го сигнала, |
||||
fi |
f0 |
& i( f , f0 |
- частота 0-го сигнала, причем f0 l / T , где l |
целое число, а |
|||||
( f |
частотный интервал, разделяющий соседние несущие. Величины ( f |
и f0 |
|||||||
должны быть выбраны так, чтобы сигналы были ортогональными. |
|
||||||||
|
|
Вид сигналов АМ |
и |
КАМ |
во |
временной области зависит от |
вида |
||
базисных функций, используемых для их представления. Предположим, что в качестве базисных функций выбраны отрезки гармоник: для АМ отрезок
синусоиды длительности T |
с частотой f0 , |
а для КАМ отрезки синусоиды и |
косинусоиды длительности |
T с частотой |
f0 . Тогда во всех рассматриваемых |
здесь видах модуляции используются сигналы представляющие собой отрезки гармонического колебания длительности T . На рис. 20.1 показаны примеры q -
ичных, q 16 , сигнальных последовательностей длины 8, соответствующих передаче одной и той же последовательности сообщений. Отметим некоторые очевидные особенности представленных сигнальных последовательностей. Сигналы ФМ и ЧМ имеют постоянную амплитуду и, следовательно, постоянную энергию. Сигналы АМ, КАМ и ФМ передаются с использованием одной несущей частоты, а для передачи ЧМ требуется несколько частот. Поэтому АМ, КАМ и ФМ относятся к узкополосным методам модуляции, а ЧМ к широкополосным. По внешнему виду сигналы АМ и КАМ близки; для АМ
существует два варианта изменения фазы в момент смены сигналов: изменение на противоположную и сохранение предыдущего значения. Для КАМ это изменение возможно в более широких переделах. Последнее утверждение справедливо и для ФМ.
Рис.20.1 Примеры сигнальных последовательностей АМ, КАМ, ФМ и ЧМ (сверху вниз)
Важным является сравнение видов модуляции по их энергетической эффективности. Рассмотрим значение отношения сигнал/шум требуемое для достижения фиксированного значения вероятности ошибки Pe , скажем
P |
10%5 , и исследуем изменение этого значения с увеличением числа сигналов |
e |
|
q |
и связанного с ним значения числа бит, переносимых одним сигналом, |
m log 2 (q) . Эти данные представлены в таблице 20.1
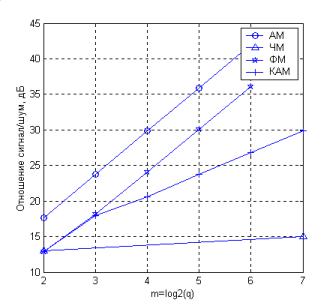
|
|
|
|
|
Таблица 20.1 |
||
|
Отношение сигнал/шум, дБ, требуемое для достижения P |
10%5 |
|||||
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
q 4 |
q 8 |
q 16 |
q 32 |
q 64 |
|
q 128 |
|
m 2 |
m 3 |
m 4 |
m 5 |
m 6 |
|
m 7 |
|
|
|
|
|
|
|
|
ЧМ |
13 |
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
АМ |
17.6 |
23.8 |
29.9 |
35.9 |
42.0 |
|
48.0 |
|
|
|
|
|
|
|
|
ФМ |
12.9 |
18.2 |
24.1 |
30.1 |
36.1 |
|
|
|
|
|
|
|
|
|
|
КАМ |
12.9 |
18.0 |
20.6 |
23.8 |
26.8 |
|
29.9 |
|
|
|
|
|
|
|
|
Из приведенных в таблице 20.1 данных следует, что для увеличения m на 1 при сохранении значения вероятности ошибки требуется увеличить отношение сигнал шум для АМ примерно на 6дБ, для ФМ тоже примерно на 6 дБ, для КАМ примерно на 3дБ. Для ЧМ это увеличение измеряется долями дБ. На рис. 20.2 приведены эти зависимости. Из приведенных данных следует, что наибольшей энергетической эффективностью обладает ЧМ, потом идут КАМ, ФМ и АМ.
Рис.20.2 Энергетическая эффективность различных видов модуляции
Рассмотрим теперь спектральную эффективность, или удельную
скорость передачи. |
Эта величина определяется как Vуд V /W , где |
V log 2 q / T m / T |
- скорость передачи, бит/с, а W - ширина полосы частот. |
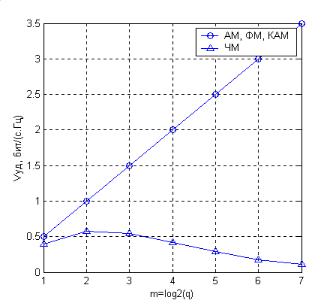
Для сигналов КАМ, АМ, ФМ, полученных на основе отрезков гармоник с прямоугольными огибающими W ) 2 / T ; заметим, что ширина полосы в этом случае не зависит от объема сигнального алфавита. Для ЧМ сигналов с прямоугольными огибающими и несущими, выбранными с постоянным шагом по частоте, W 2 / T & (q %1)( f , где ( f - частотный интервал между соседними
несущими. Известно, что минимальное значение ( f 1/(2T ) (в общем случае
для обеспечения ортогональности сигналов ЧМ нужно чтобы выполнялось условие ( f l /(2T ) , где l целое). Тогда для полосы частот, занимаемой ЧМ
сигналами, имеем выражение |
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
2 |
|
& |
q %1 |
|
|
q & 3 |
|
2m & 3 |
. |
|||
T |
|
|
|
|
|||||||||
|
|
|
|
2T |
|
|
|
2T |
2T |
||||
В итоге |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−m |
, |
для КАМ, АМ, ФМ |
||||||||||
|
|
|
|
||||||||||
|
2 |
||||||||||||
Vуд , |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2m |
|
, |
|
для ЧМ |
|
|
||||
|
2m & |
3 |
|
|
|
||||||||
|
+ |
|
|
|
|
|
|
|
|||||
Графики для удельной скорости передачи для этих видов модуляции показаны на рис. 20.3.
Рис.20.3 Спектральная эффективность различных видов модуляции
Из приведенного графика видно, что наименьшей спектральной эффективностью (удельной скоростью передачи) обладает ЧМ, а КАМ, АМ и ФМ по этому показателю эквивалентны. Таблица 20.2 содержит основные параметры сигналов рассмотренных видов модуляции.
Таблица 20.2
Основные параметры сигналов АМ, КАМ, ФМ и ЧМ
|
Скорость |
Постоянная |
Полоса |
Vуд , |
Место по |
Место по |
Размерность |
|||||
|
V , бит/с |
амплитуда |
W , Гц |
бит/(c.Гц) |
энергетич. |
спектр. |
|
|||||
|
|
|
|
|
|
|
эффект. |
эффект. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
АМ |
log2 |
q / T |
- |
2 / T |
m / 2 |
4 |
1-3 |
1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
КАМ |
log2 |
q / T |
- |
2 / T |
m / 2 |
2 |
1-3 |
2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ФМ |
log2 |
q / T |
+ |
2 / T |
m / 2 |
3 |
1-3 |
2 |
||||
|
|
|
|
|
|
|
|
|
|
|
||
ЧМ |
log2 |
q / T |
+ |
|
q & 3 |
|
2m |
1 |
4 |
q |
||
|
|
|
|
|
2T |
|
|
2m & 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

20-1. Частотное разделение с использованием ортогональных несущих
(OFDM)
Сигналы OFDM (OFDM = Orthogonal Frequency Division Multiplexing)
формируются как сумма сигналов КАМ (или ФМ), передаваемых на различных несущих частотах. Общая полоса частот, отведенная для передачи, делится на N параллельных частотных подканалов, число которых на практике может лежать в пределах от нескольких десятков до нескольких тысяч. В подканале с номером n , n = 0,1,..., N −1, передается сигнал вида
|
si(n) (t) = si(1n) |
2 cos 2πfn t + si(2n) |
2 sin 2πfn t , 0 ≤ t ≤ T , |
(20-1.1) |
|
|
T |
T |
|
где T – |
длительность |
сигнала, fn – |
несущая частота1, используемая для |
|
передачи |
в n -ом частотном подканале, |
i = 0,1,...qn −1, qn – число сигналов, |
||
используемых в n -ом подканале. На практике все величины qn обычно равны между собой, но в общем случае они могут быть различными: например, в части подканалов может использоваться КАМ-16, а в другой части подканалов КАМ-4. Пара коэффициентов (si(1n) , si(2n) ) находится во взаимно-однозначном
соответствии с индексом i |
и определяет i -ую точку в двумерном сигнальном |
||
созвездии КАМ или ФМ, используемом в n -ом подканале. |
|
||
Обозначим |
индекс сигнала передаваемого в n -ом подканале |
как in , |
|
in = 0,1,2,..., qn −1. |
Пусть i |
– набор этих индексов (мультииндекс), |
то есть |
i = (i0 ,i1 ,...,iN −1 ) . |
Тогда |
совокупный OFDM сигнал, соответствующий |
|
мультииндексу i , определяется как сумма сигналов в подканалах |
|
||
|
|
N −1 |
|
|
|
si (t) = ∑si(nn) (t) |
(20-1.2) |
|
|
n=0 |
|
Общее число OFDM сигналов q равно числу различных мультииндексов i , то
есть q = q0 q1...qN −1 . Значение мультииндекса может рассматриваться как сообщение, подлежащее передаче. Тогда очевидно, что скорость передачи (информационная скорость) равна
1 Эти частоты иногда называют поднесущими частотами (subcarrier)

|
1 |
|
1 |
N −1 |
|
V = |
log2 q = |
∑log2 qn , бит/с. |
|||
|
|
||||
|
T |
T n=0 |
|||
Передаваемое сообщение представляет собой значение мультииндекса, то есть
блок |
из |
∑nN=−01log2 qn |
бит. |
Он разбивается на |
N подблоков длиной log2 qn , |
||
n = 0,1,2,..., N −1, и n -ый |
подблок, то есть величина |
in задает номер |
пары |
||||
(s(n) , s(n) ) , |
которая определяет КАМ или ФМ сигнал, |
передаваемый в |
n -ом |
||||
i1 |
i2 |
|
|
|
|
|
|
подканале. Очевидно, |
что один сигнал OFDM |
может переносить много бит |
|||||
информации. Например, при числе подканалов |
N = 64 |
и КАM-16 в каждом |
|||||
подканале |
сигнал OFDM переносит N log2 q0 |
= 64 4 = 256 бит. Значение |
|||||
мультииндекса представляет собой в этом случае любую 256-битную последовательность.
|
Несущие |
частоты |
fn |
выбираются так, чтобы подканалы были |
||||
ортогональными, то есть чтобы выполнялись условия |
|
|||||||
T |
|
|
|
T |
|
|
|
1, n = k |
∫ |
2 / T cos 2πfnt |
2 / T cos 2πfk tdt = ∫ |
2 / T sin 2πfnt |
|
||||
2 / T sin 2πfk tdt = |
||||||||
0 |
|
|
|
0 |
|
|
|
0, n ≠ k |
и |
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
∫ |
2 / T cos 2πfnt |
2 / T sin 2πfk tdt = 0 для всех n,k . |
|
||||
|
0 |
|
|
|
|
|
|
|
Это условие достигается, если |
fn = f0 + n∆ f , где |
f0 = l0 / T , l0 |
– целое число |
|||||
или |
l0 >>1, и ∆ f |
= l / T , l |
– |
целое. Минимальный шаг по частоте ∆f , при |
||||
котором достигается ортогональность подканалов, |
равен 1/T . |
Тогда полоса |
||||||
частот, занимаемая совокупным OFDM сигналом, равна |
|
|||||||
|
W = 2 /T +(N −1)∆f = 2 /T +(N −1) /T = (N +1) /T . |
|
||||||
Отсюда следует, что OFDM сигналы являются широкополосными2 сигналами; |
||||||||
их спектр лежит в диапазоне от f0 −1/ T до |
f0 + N / T . |
|
||||||
|
Удельная скорость передачи (эффективность использования полосы) при |
|||||||
использовании OFDM равна |
|
|
|
|
|
|
||
|
|
|
|
|
1 |
N −1 |
|
|
|
|
Vуд =V /W = |
∑log2 qn . |
|
||||
|
|
|
|
|||||
|
|
|
|
|
N +1 n=0 |
|
|
|
2 Напомним, что широкополосными называются сигналы, для которых WT >>1.
Рассмотрим частный случай, когда во всех подканалах передается одинаковое число сигналов, то есть qn = q0 , n =1,2,..., N −1 . Тогда
Vуд = |
|
N |
|
log2 q0 → log2 q0 = m при N >>1. |
|
N +1 |
|||||
|
|
||||
Последнее соотношение означает, что OFDM обладает очень высокой удельной |
|||||
скоростью, то есть очень |
эффективно использует полосу частот (ср. с |
||||
данными, приведенными в Табл. 20.2). |
|||||
В канале с АБГШ |
вероятность ошибки при оптимальном приеме OFDM |
||||
сигналов может быть легко оценена. Поскольку несущие частоты в подканалах выбраны так, что обеспечивается ортогональность, то искажения, возникающие из-за влияния АБГШ, независимы в различных подканалах. Поэтому вероятность ошибки (вероятность неправильного определения значения мультииндекса i на приемной стороне) легко может быть найдена следующим образом
N −1
Pe =1 −∏(1 − Pe(n) ) ,
n=0
где Pe(n) - вероятность ошибки в n − ом подканале, то есть вероятность ошибки КАМ или ФМ сигналов (см. соответствующие выражения в разделах о КАМ и ФМ).
Формирование и прием OFDM сигналов. Формирование и прием OFDM
сигналов может выполняться:
–непосредственным путем по формулам (20-1.1) и (20-1.2);
–более эффективным цифровым способом с использованием быстрого преобразования Фурье (БПФ), (Fast Fourier Transform, FFT) .
Идея цифрового способа формирования OFDM сигнала состоит в том, что в цифровой форме вычисляются значения отсчетов сигнала в моменты
времени t = 0, T / N, 2T / N,..., (N −1)T / N , а затем с помощью цифро-
аналогового преобразования и интерполяции восстанавливается сигнал в непрерывной форме. Рассмотрим этот алгоритм более подробно.
Сигнал OFDM имеет вид
si (t) = |
2 |
N −1 |
(n) |
(n) |
sin 2πfnt). |
|
∑(sin 1 |
cos 2πfnt + sin 2 |
|||
|
T n=0 |
|
|
|
|
Обозначим X i(n) = si(n1) |
− jsi(n2) . Покажем, что |
|
|
|
|
||||||
|
|
|
n |
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
N −1 |
|
|
|
|
|
|
|
|
|
|
si (t) = 2 /T Re∑X i(nn)e j 2πfnt . |
|
|
(20-1.3) |
||
Действительно, |
|
|
n=0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
N −1 |
|
− j 2πfnt |
|
N −1 |
|
|
|
|
|
|
|
(n) |
e |
|
(n) |
|
(n) |
|
|
|
|
|
|
∑X in |
|
= ∑(sin 1 |
− jsin 2 )(cos 2πfnt + j sin 2πfnt)= |
|
|
|
|||||
n=0 |
|
|
|
n=0 |
|
|
|
|
|
|
|
|
|
|
|
N −1 |
(n) |
(n) |
|
N −1 |
|
(n) |
sin 2πfnt), |
|
|
|
|
|
|
(n) |
|
||||
|
|
|
|
= ∑(sin 1 |
cos 2πfnt + sin 2 |
sin 2πfnt)+ j∑(− sin 2 |
cos 2πfnt + sin 1 |
||||
|
|
|
|
n=0 |
|
|
|
n=0 |
|
|
|
откуда следует выражение (20-1.3). Поскольку |
fn = f0 +n∆f |
= f0 +n /T , где |
|||||||||
n = 0,1,..., N −1, то из (20-1.3) следует, что |
|
|
|
|
|||||||
|
|
|
|
N −1 |
|
|
N −1 |
|
|
|
|
si (t) = 2 /T Re∑X i(nn)e j 2πf ( f0 +n / T )t |
|
|
(20-1.4) |
||||||||
= Re 2 /T e j 2πf0t ∑X i(n)e j 2π (n / T )t . |
|||||||||||
Обозначим |
|
n=0 |
|
|
|
n=0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
N −1 |
|
|
|
|
|
|
|
|
|
|
|
xi (t) = ∑X i(nn)e j 2π (n / T )t |
. |
|
|
(20-1.5) |
|
|
|
|
|
|
|
n=0 |
|
|
|
|
|
Функция xi (t) принимает комплексные значения и может быть представлена в виде xi (t) = Re xi (t) + j Im xi (t) . Тогда из равенств (20-1.4) и (20-1.5) следует,
что
si (t) = Re(( 2 /T cos 2πf0t + j
2 /T cos 2πf0t + j  2 /T sin 2πf0t)(Re xi (t) + j Im xi (t)))=
2 /T sin 2πf0t)(Re xi (t) + j Im xi (t)))=
|
= Re xi (t) |
2 /T cos 2πf0t −Im xi (t) |
2 /T sin 2πf0t . |
Последнее выражение означает, что для формирования OFDM сигнала, |
|||
зависящего от значения мультииндекса i , |
нужно уметь вычислять значения |
||
функций Re xi (t) и Im xi (t) для 0 <t <T . |
|
|
|
Рассмотрим отсчеты |
функции |
xi (t) в моменты |
t = kT / N , |
k = 0,1,..., N −1, то есть величины |
|
|
|
N −1
xi (t) t=kT / N = xi(k ) = ∑X i(n)e j 2πnk / N . n=0
Тогда легко заметить, что комплексный вектор xi = (xi(0) , xi(1) ,..., xi( N −1) )
представляет собой дискретное преобразование Фурье (ДПФ)3 комплексного
3 Прямое и обратное ДПФ определяются как
N −1 |
|
1 |
N −1 |
|
X (n) = ∑x(k )e− j 2πnk / N |
и x(k ) = |
∑X (n)e j 2πnk / N соответственно. |
||
|
||||
k =0 |
|
N n=0 |
||
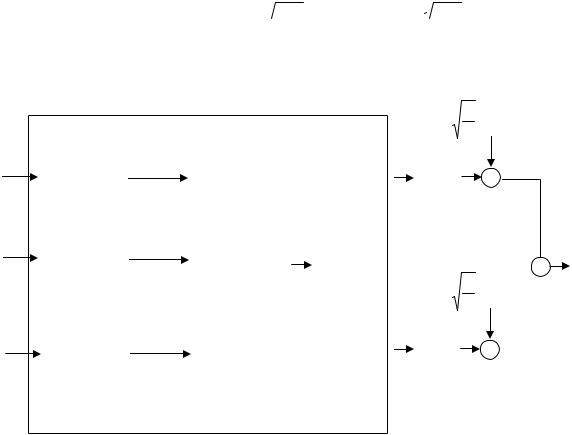
вектора Xi = (X i(0) , X i(1) ,..., X i( N −1) ). При определенных значениях длины преобразования N , в частности когда N = 2 p , p - целое, получение вектора xi
из вектора Xi может быть выполнено очень эффективно с использованием быстрого преобразования Фурье (БПФ).
Поэтому формирование OFDM сигнала выполняется так:
– по значению мультииндекса i вычисляются величины X i(n) , n = 0,1,....N −1, (отображение КАМ или ФМ) и формируется вектор Xi = (X i(0) , X i(1) ,..., X i( N −1) );
–по вектору Xi вычисляется комплексный вектор xi (быстрое ДПФ);
–по Re xi и Im xi восстанавливаются непрерывные сигналы Re xi (t) и Im xi (t) (цифро-аналоговое преобразование и интерполяция);
–формируется OFDM сигнал как Re xi (t) 2 /T cos 2πf0t −Im xi (t)
2 /T cos 2πf0t −Im xi (t)  2 /T sin 2πf0t .
2 /T sin 2πf0t .
Иллюстрация показана на рис.20-1.1.
|
|
|
|
|
|
|
|
|
|
|
|
|
2 cos 2πf0t |
||||
i0 |
|
|
(si 1 |
, si 2 ) |
|
|
|
|
|
|
|
T |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
КАМ (ФМ) |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Re xi |
|
|
ЦАП |
× |
|
|
|
|
||
i1 |
|
отображение |
(si11 |
, si2 |
2 ) |
|
|
|
|
|
|
|
s (t) |
||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
КАМ (ФМ) |
Формирование |
|
|
xi |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отображение |
|
|
|
вектора Xi |
|
ОБПФ |
|
|
|
|
+ |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
− |
2 sin 2πf0t |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
iN −1 |
|
(siN −11 , siN −1 2 ) |
|
|
|
|
|
|
|
T |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
КАМ (ФМ) |
|
|
|
|
|
Imxi |
|
|
|
× |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
ЦАП |
|
|
|
|
||||
|
|
отображение |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Цифровая обработка
Рис. 20-1.1 Схема формирования OFDM сигнала
Рассмотрим поясняющий пример со значениями параметров близкими к реальным (стандарт IEEE 802.11b для локальных беспроводных сетей). Пусть
число подканалов N = 64 и в каждом подканале используется КАМ-16. Пусть частотный интервал между соседними несущими равен ∆ f = 312.5кГц,
следовательно, длительность сигнала равна T =1/ 312500 =3.2мкс. Положим также значение минимальной несущей f0 = 2.4 ГГц. Каждый сигнал переносит в этом случае 64 ×log 2 16 = 256 бит за время 3.2 мкс, то есть скорость передачи составляет 80 Мбит/с. Заметим, что реальная скорость передачи, обеспечиваемая стандартом, значительно меньше указанного значения из-за потерь в скорости требуемых для обеспечения работы всей системы (временные защитные интервалы, управление, помехоустойчивое кодирование и др.). На рис. 20-1.2 и 20-1.3 показаны графики, иллюстрирующие формирование OFDM сигнала с указанными параметрами для некоторого случайного информационного набора из 256 бит.
a) |
Re |
xi, Re xi(t) |
|
0.5 |
|
|
|
0 |
|
|
|
-0.5 |
|
|
|
0 |
1 |
2 |
3 |
|
|
t, c |
-6 |
|
|
|
x 10 |
c) |
Re xi(t) cos2πf0t |
|
|
0.5 |
|
|
|
0 |
|
|
|
-0.5 |
|
|
|
0 |
1 |
2 |
3 |
|
|
t, c |
-6 |
|
|
|
x 10 |
b) |
Im |
xi, Im xi(t) |
|
1 |
|
|
|
0.5 |
|
|
|
0 |
|
|
|
-0.5 |
|
|
|
-1 |
|
|
|
0 |
1 |
2 |
3 |
|
|
t, c |
-6 |
|
|
|
x 10 |
d) |
Im xi(t) sin2πf0t |
|
|
1 |
|
|
|
0.5
0
-0.5
-1
0 |
1 |
2 |
3 |
|
|
t, c |
-6 |
|
|
|
x 10 |
Рис. 20-1.2 Компоненты OFDM сигнала. Пример.
|
|
|
si(t) |
|
|
|
1 |
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
-0.5 |
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
|
|
|
t, c |
|
|
-6 |
|
|
|
|
|
|
x 10 |
Рис.20-1.3 Пример OFDM сигнала
Схема приемника OFDM сигнала показана на рис. 20-1.4
|
2 cos 2πf0t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rc |
|
|
|
|
|
ˆ (0) |
|
|
iˆ0 |
|
|
× |
|
ФНЧ |
|
АЦП |
|
|
|
|
|
X |
Решение |
|
|||
|
|
|
|
|
|
|
|
|
ˆ (1) |
КАМ (ФМ) |
ˆ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
X |
Решение |
i1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
r(t) |
|
|
|
|
|
|
Формирование |
|
|
ˆ |
|
|
|
КАМ (ФМ) |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вектора |
|
|
X |
|
|
|
|
|
|
|
2 sin 2πf0t |
|
|
|
|
rc + jrs |
|
БПФ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
iN −1 |
|
|
|
|
|
|
|
rs |
|
|
|
|
ˆ |
|
|
|
|
|
|
× |
|
ФНЧ |
|
АЦП |
|
|
|
|
X |
( N −1) |
|
Решение |
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
КАМ (ФМ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Цифровая обработка
Рис. 20-1.4. Схема приема OFDM сигнала
Поясним работу этой схемы. После умножения принятого сигнала на гармонические функции и НЧ фильтрации получаются низкочастотные компоненты сигнала. Они соответствуют непрерывным функциям, показанным на частях а) и b) рис. 20-1.2. Аналого-цифровые преобразования
формируют векторы rc |
и rs , состоящие из |
N отсчетов. Из векторов rc |
и rs |
||||||
строится |
комплексный |
вектор |
rc + jrs и |
подвергается обратному |
|||||
преобразованию Фурье (БПФ). |
В результате получается комплексный вектор |
||||||||
ˆ |
ˆ (0) |
ˆ (1) |
ˆ ( N −1) |
) . |
По |
величинам |
ˆ (n) |
строятся решения |
ˆ |
X = (X |
, X |
,..., X |
X |
in , |
|||||
n = 0,1,..., N −1.

21. Тактовая синхронизация. Устройство установления тактовой синхронизации
Схема оптимального приемника содержит корреляторы либо
согласованные фильтры, соединенные |
с устройством взятия отсчетов (см. рис. |
||||||||||||
21.1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
si (t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
! dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h (t) |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
а) |
|
|
|
б) |
|||||
Рис.21.1 Коррелятор (а) и согласованный фильтр с устройством взятия отсчетов (б).
Работа этих устройств должна быть синхронизирована с поступающей из канала последовательностью: должны быть точно известны моменты начала и конца интегрирования в случае использования корреляторов или моменты взятия отсчетов при использовании приемника с согласованными фильтрами. В обоих случаях достаточным будет знание в точке приема моментов времени T,2T,3T,4T,... . Получение этих моментов времени (“меток времени”)
называется синхронизацией. Возможны следующие подходы к установлению синхронизации: 1) использование общего внешнего источника сигналов точного времени для передатчика и приемника; 2) передача меток времени по отдельному каналу; 3) получение меток времени из принятой сигнальной последовательности. Очевидно, что наиболее практически значимым является третий подход. Иллюстрация показана на рис.21.2.
Существует ряд подходов к решению задачи установления тактовой синхронизации. Рассмотрим один из них. Ограничимся случаем передачи двоичных противоположных сигналов по каналу с АБГШ.
r(t)
Оптимальный
приемник
Устройство
установления
синхронизации
Метки времени
T 2T 3T 4T 5T …
Рис.21.2 Установление синхронизации по принятому сигналу
Предположим, что временной сдвиг (ошибка синхронизации) # |
равномерно |
распределен на интервале [0,T ] , и на интервале наблюдения NT |
этот сдвиг |
постоянен. Возьмем на длительности сигнала n отсчетов и будем оценивать этот временной сдвиг с точностью до величины T / n , то есть будем оценивать
величину |
# m mT / n , где m 0,1,..., n %1. Обозначим |
значение |
i -го отсчета |
||||
принятого |
сигнала на |
j % ом интервале наблюдения |
как r (ij) , |
j 1,2,..., N , |
|||
i 1,2,.., n . |
Обозначим |
последовательность отсчетов |
принятой |
сигнальной |
|||
последовательности как |
|
|
|
|
|
|
|
|
r (r (11) , r (21) ,..., r ( n1) , r (12) , r (22) ,..., r (n2) ,..., r (1N ) , r (2 N ) ,..., r ( nN ) ) . |
||||||
Можно записать также, |
что |
r (r (1) , r ( 2) ,..., r ( N ) ) , |
где |
r ( j) |
(r (1 j) , r ( 2 j) ,..., r (nj) ) . |
||
Обозначим также отсчеты |
сигнала в пределах |
одного |
j -го |
сигнального |
|||
интервала как s(ij) (# m ) . Каждый отсчет выходного сигнала канала может быть записан как
|
|
|
|
|
|
r (ij) s(ij) (# m ) & n(ij) , |
|
|
|
|||
где |
n(ij) |
- отсчет |
шума, |
соответствующий |
i -му |
отсчету |
j -го сигнала в |
|||||
последовательности. Все n(ij) - |
независимые гауссовские случайные величины, |
|||||||||||
|
|
0 , |
|
|
2 . |
|
|
|
||||
и |
n(ij) |
(n(ij) )2 |
Обозначим |
вектор |
отсчетов сигнальной |
|||||||
последовательности, |
|
взятых |
в |
пределах |
j -го |
интервала, |
как |
|||||
s( j) (# m ) (s(1 j ) (# m ), s(2 j ) (# m ),..., s(nj ) (# m )) .
Оптимальное решение (решение по максимуму апостериорной вероятности) относительно # m вычисляется как

!
# m arg max P(# m | r) ,
# m
где |
P(# m | r) - апостериорное распределение величины # m , |
m 0,1,..., n %1. По |
||||||||
формуле Байеса имеем |
|
|
|
|
|
|
|
|
||
|
|
|
P(# m | r) |
P(# m ) |
w(r | # m ) . |
|
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
w(r) |
|
|
|
||
Поскольку величина # m распределена |
равномерно, |
то есть P(# m ) 1/ n , то |
||||||||
очевидно, что оптимальная оценка может быть получена как |
|
|||||||||
|
|
|
! |
|
|
|
|
|
|
(21.1) |
|
|
|
# m arg max w(r | # m ) . |
|
|
|||||
|
|
|
|
|
# m |
|
|
|
|
|
Плотность вероятностей w(r | # m ) может быть записана как |
|
|||||||||
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
w(r | # m ) ( w(r ( j ) | # m ) . |
|
|
|
||||
|
|
|
|
|
j 1 |
|
|
|
|
|
Для |
плотности w(r ( j ) |
| # m ) имеем следующее выражение |
(формула полной |
|||||||
вероятности) |
|
|
|
|
|
|
|
|
|
|
|
w(r ( j ) | # |
m |
) w(r ( j) | 0,# |
m |
)P |
& w(r ( j ) | 1,# |
m |
)P , |
(21.2) |
|
|
|
|
0 |
|
|
1 |
|
|||
где |
P0 , P1 - вероятности передачи нуля и единицы соответственно, w(r | 0,# m ) , |
|||||||||
w(r | 1,# m ) - условные плотности вероятностей величины r при передаче нуля и
единицы |
|
|
при |
фиксированном |
|
временном |
|
сдвиге |
# m . |
|
При |
|
передаче |
|||||||||||||||||||
противоположных сигналов в канале с АБГШ имеем |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
w(r ( j ) | 0,# |
|
|
) |
n |
|
1 |
|
. |
(r (ij) % s(ij) (# |
|
))2 |
+ |
. |
|
n |
(r (ij) % s(ij) (# |
|
))2 |
+ |
|||||||||||||
m |
( |
|
2 |
exp, % |
|
|
|
|
2 |
m |
|
|
) |
K exp, % |
/ |
|
|
|
|
2 |
m |
|
|
) |
||||||||
|
|
|
20 |
, |
|
|
2 |
|
|
|
) |
, |
|
|
|
2 |
|
|
|
) |
||||||||||||
|
|
|
|
|
i 1 |
|
|
− |
|
|
|
|
|
|
|
|
− |
|
i 1 |
|
|
|
|
|
|
|
|
|||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w(r ( j ) | 1,# |
|
|
) |
n |
|
1 |
|
. |
(r |
(ij) |
& s |
(ij) |
(# m )) |
2 |
+ |
. |
|
n |
(r |
(ij) |
& s |
(ij) |
(# m )) |
2 |
+ |
|||||||
|
|
|
|
exp, % |
) |
K exp, % |
) |
|||||||||||||||||||||||||
|
m |
|
|
( |
|
20 |
2 |
, |
|
|
2 |
2 |
|
|
|
|
) |
, |
|
/ |
|
|
2 |
2 |
|
|
|
|
) |
|||
|
|
|
|
|
i 1 |
|
|
− |
|
|
|
|
|
|
|
|
− |
|
i 1 |
|
|
|
|
|
|
|
|
|||||
где K = (2πσ 2 )−n / 2 . При записи этих выражений учтено, что отсчеты сигналов,
соответствующих передаче нуля и единицы, различаются только знаком. Далее, с учетом этих выражений из равенства (21.2) следует, что
|
|
N |
|
|
n |
(r |
(ij ) |
− s |
(ij ) |
(τm )) |
2 |
|
|
n |
(r |
(ij ) |
+ s |
(ij ) |
(τm )) |
2 |
|
|
||
w(r | τm ) = K |
N |
|
|
|
− ∑ |
|
|
|
|
|
|
− ∑ |
|
|
|
|
|
, |
||||||
|
∏ P0 |
exp |
|
|
2σ |
2 |
|
|
|
+ P1 exp |
|
|
2σ |
2 |
|
|
|
|||||||
|
|
j=1 |
|
i=1 |
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
||||||
Полагая сигналы равновероятными, то есть P0 = P1 =1/ 2 , получим
N |
1 |
|
n |
r (ij) s(ij ) (τ |
m |
) |
|
1 |
n |
r (ij) s(ij ) (τ |
m |
) |
|
|
||||
|
|
|
− ∑ |
|
|
|
|
+ |
|
|
|
|
|
|
, |
(21.3) |
||
|
|
2 |
|
|
|
|
2 |
|
|
|||||||||
w(r | τm ) = K1 (r)∏ |
2 |
exp |
σ |
|
|
|
2 |
exp ∑ |
σ |
|
|
|
||||||
j=1 |
i=1 |
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|||||
где
N |
|
n |
(r |
(ij) |
) |
2 |
+ (s |
(ij) |
(τm )) |
2 |
|
|
|
|
− ∑ |
|
|
|
|
|
|
||||
K1 (r) = ∏K exp |
|
|
|
|
|
|
|
|
|
, |
||
|
|
|
|
2σ |
2 |
|
|
|||||
j=1 |
|
i=1 |
|
|
|
|
|
|
|
|
|
|
множитель, не зависящий от величины τm . Используя определение функции гиперболического косинуса cosh(x) = (ex + e−x ) / 2 , получим из (21.3)
N |
|
n |
r |
(ij) |
s |
(ij) |
(τm ) |
|
|
|
|
∑ |
|
|
|
|
|||
|
|
|
|
|
2 |
|
|||
w(r |τm ) = K1 (r)∏cosh |
|
|
σ |
|
. |
||||
j=1 |
i=1 |
|
|
|
|
|
|||
Поэтому, оптимальная оценка величины временного сдвига может быть получена как
) |
N |
|
n |
r |
(ij) |
s |
(ij) |
(τm ) |
|
|
|
N |
n |
r |
(ij) |
s |
(ij) |
(τm ) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
τm = arg maxτ |
|
∑ |
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|||||
∏cosh |
|
|
σ |
|
|
= arg maxτ |
∑log cosh ∑ |
|
|
σ |
|
. |
|||||||||
m |
j=1 |
i=1 |
|
|
|
|
|
|
m |
j=1 |
i=1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
∆ |
n |
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим величину Y ( j) (τm ) =∑r(ij) s(ij ) (τm ) . Нетрудно заметить, что |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
jT −τm |
|
|
|
|
|
|
|
|
|
Y ( j) (τm ) = ∑r (ij ) s(ij) (τm ) ≈ C |
∫r(t)s(t − ( j −1)T +τm )dt , |
|
|||||||||||||||||||
|
|
|
i=1 |
|
|
|
|
|
|
|
( j−1)T −τm |
|
|
|
|
|
|
|
|
||
где C - некоторая константа; то есть это значение пропорциональное Y ( j) (τm )
может быть вычислено с использованием коррелятора, похожего на показаный

на рис.21.1а. Ранее отмечалось, что коррелятор может быть реализован с использованием согласованного фильтра. Пусть h(t) s(T % t) импульсная переходная характеристика фильтра согласованного с сигналом s(t) . Заметим,
что импульсная переходная характеристика фильтра h(t) имеет конечную длительность. Обозначим сигнал на выходе согласованного фильтра как y(t) .
Он равен
y(t) r(t) 4 h(t) 3!r(t1 )h(t % t1 )dt1 3!r(t1 )s(T % t & t1 )dt1 .
%3 %3
С учетом конечной длительности импульсной переходной характеристики фильтра имеем
t
y(t) !r(t1 )s(T % t & t1 )dt1
t%T
Тогда очевидно, что Y ( j ) (# m ) Cy( jT %# m ) , то есть требуемое значение может быть получено как отсчет сигнала на выходе согласованного фильтра, взятый в момент jT %# m .
Таким образом, устройство установления синхронизации должно иметь в своем составе согласованный фильтр, нелинейный элемент с характеристикой log cosh(5) , устройства взятия отсчетов, накопители и блок выбора максимума.
Схема показана на рис.21.3. Заметим, что нелинейная функция log cosh(5) на практике с успехом может быть заменена более простой в реализации функцией взятия модуля | 5 | . Основанием для такой замены является соотношение log cosh(x) 2 x % log 2 при не слишком малых x .

log cosh(5)
h(t)  или
или
| 5 |
Замыкание в моменты
|
jT %#0 |
|
|
|
|
|
|
|
|
||||
|
|
|
Накопление |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N отсчетов |
|
|
|
|
|
|
Замыкание в |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
моменты |
|
|
|
|
|
|
|
|
||||
|
jT %#1 |
|
|
|
|
|
Выбор |
! |
|||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
Накопление |
|
|
|
#m |
|
|
|
|
|
|
|
|
|
|
|
максимума |
|
|
|
|
|
|
|
|
|
|
|
N отсчетов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замыкание в моменты
jT %# n%1
Накопление  N отсчетов
N отсчетов
Рис.21.3 Устройство оптимальной оценки временного сдвига
22. Влияние неточности тактовой синхронизации на вероятность ошибки
Предположим, что синхронизация установлена с ошибкой τ . Оценим влияние неточно установленной синхронизации на вероятность ошибки. Как и прежде ограничимся рассмотрением двоичной передачи с использованием
противоположных сигналов. Обозначим si (t) = Aiϕ(t) , где A0 = − E , A1 =
E , A1 =  E ,
E ,
ϕ(t) - нормированная функция, определенная на интервале [0,T ] . При синхронизации, установленной с ошибкой τ , приемник может быть описан схемой, показаной на рис.22.1. Заметим, что при τ = 0 эта схема в точности соответствует оптимальному приемнику.
ϕ(t −τ)
r(t) |
|
|
|
i |
T +τ |
|
Сравнение |
||
|
|
|||
|
|
|
||
× |
∫dt |
|
с нулевым |
|
|
τ |
|
порогом |
|
|
|
|
|
|
Рис.22.1 Оптимальный прием противоположных сигналов при неточно установленной синхронизации
Рассмотрим передачу двух последовательно идущих сигналов. Их можно
описать как A(1)ϕ(t) и A( 2)ϕ(t −T ) , где A(1) , A(2) - амплитуды текущего и следующего сигналов соответственно, A(1) , A( 2) = ± E . Пусть n(t) как обычно
E . Пусть n(t) как обычно
обозначает АБГШ. Тогда величина на выходе коррелятора может быть найдена
как
T +τ |
T |
T +τ |
ξτ = ∫r(t)ϕ(t −τ)dt =A(1) |
∫ϕ(t)ϕ(t −τ)dt + A(2) |
∫ϕ(t −T )ϕ(t −τ)dt + n , |
τ |
τ |
T |
где n = ∫τT +τ n(t)ϕ(t −τ)dt |
- гауссовская с.в. с нулевым средним |
и дисперсией |
|||||
N0 / 2 . Для |
дальнейшего |
рассмотрения |
требуется ввести |
некоторые |
|||
обозначения. |
Пусть |
|
|
|
|
|
|
|
|
|
Rτ(1) = ∫τT ϕ(t)ϕ(t −τ)dt |
|
(22.1) |
||
и |
|
|
|
|
|
|
|
|
|
|
Rτ(2) = ∫TT +τ ϕ(t −T )ϕ(t −τ)dt . |
|
(22.2) |
||
Очевидно, что R(1) =1 , |
R(2) |
= 0 , R(1) = 0 , |
R(2) |
=1. |
|
|
|
|
0 |
0 |
T |
T |
|
|
|
Оценим вероятность ошибки. Как обычно сигналы предполагаются |
|||||||
равновероятными, поэтому |
Pe = (Pe (0) + Pe (1)) / 2 , где Pe (0) , |
Pe (1) |
условные |
||||
вероятности ошибки при передаче нуля и единицы соответственно. Рассмотрим вероятность Pe (0) . Легко видеть, что при передаче нуля и при фиксированном
значении амплитуды следующего за текущим сигнала вероятность ошибки равна
Pe (0, A(2) ) = Pr[ξτ > 0 | 0, A(2) ] = Pr[−  ERτ(1) + A( 2) Rτ(2) + n > 0].
ERτ(1) + A( 2) Rτ(2) + n > 0].
Поскольку амплитуда A(2) равновероятно принимает значения ±  E , то после
E , то после
усреднения по этим значениям имеем
Pe (0) = (1/ 2) Pr[−  E (Rτ(1) + Rτ( 2) ) + n > 0]+ (1/ 2) Pr[−
E (Rτ(1) + Rτ( 2) ) + n > 0]+ (1/ 2) Pr[−  E (Rτ(1) − Rτ(2) ) + n > 0].
E (Rτ(1) − Rτ(2) ) + n > 0].
Отсюда следует, что
P (0) = |
1 |
|
2E |
(R |
(1) |
+ R |
(2) |
|
+ |
1 |
|
2E |
(R |
(1) |
− R |
(2) |
|
|
Q |
|
|
|
) |
|
Q |
|
|
|
) . |
||||||
e |
2 |
|
N0 |
τ |
τ |
|
|
2 |
|
N0 |
τ |
τ |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Правая часть этого выражения не зависит от номера переданного сигнала; это значит, что условная вероятность ошибки в данном случае совпадает с безусловной, то есть

P |
= |
1 |
|
2E |
(R |
(1) |
+ R |
(2) |
|
+ |
1 |
|
2E |
(R |
(1) |
− R |
(2) |
|
(22.3) |
|
Q |
|
|
|
) |
|
Q |
|
|
|
) . |
||||||||
e |
2 |
|
N0 |
τ |
τ |
|
|
2 |
|
N0 |
τ |
τ |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вероятность ошибки, как это следует из выражения (22.3), зависит от
отношения сигнал/шум и косвенно, |
то есть через величины Rτ(1) и Rτ(2) , от |
||
временного сдвига τ и формы сигналов. |
|
|
|
Рассмотрим частный случай. Пусть сигналы представляют собой |
|||
противоположные прямоугольные импульсы, то есть |
|||
|
1 |
, 0 |
< t < T |
|
T |
||
|
|
. |
|
ϕ(t) = |
|
|
|
|
|
|
|
|
|
|
|
0, иначе |
|||
Тогда с использованием |
определений |
(22.1) |
и |
(22.2), легко |
показать, что |
|||||||
Rτ(2) =τ / T , Rτ(1) = (T −τ) / T . Отсюда |
|
|
|
|
|
|
|
|
||||
P = |
1 |
|
2E |
+ |
1 |
|
|
2E |
|
− |
2τ |
(22.4) |
|
Q |
|
|
Q |
|
1 |
. |
|||||
e |
2 |
|
|
|
2 |
|
|
N0 |
|
|
|
|
|
|
N0 |
|
|
|
|
T |
|
||||
Аналогичное выражение можно получить, если рассмотреть не положительное,
а отрицательное значение временного сдвига τ . В итоге будет получена формула, совпадающая с (22.4) , в которой вместо τ будет −τ . Окончательное выражение, учитывающее как положительную ошибку синхронизации
(опоздание) так и отрицательную (опережение), имеет вид
P = |
1 |
|
2E |
+ |
1 |
|
2E |
− |
2 | τ | |
|
|
Q |
|
|
Q |
1 |
|
. |
|||
e |
2 |
|
|
|
2 |
|
N0 |
|
T |
|
|
|
N0 |
|
|
|
|
||||
Графики вероятности ошибки для различных величин отношения τ / T
показаны на рис.22.1. Видно, что при увеличении этого отношения вероятность ошибки убывает с ростом отношения сигнал/шум все медленнее, а при
τ / T =1/ 2 передача становится невозможной.

Рис.22.1 Вероятность ошибки для двоичных противоположных сигналов при различных значениях ошибки синхронизации
23. Канал с аддитивным белым гауссовским шумом и случайной фазой
Основной моделью канала, рассматривавшейся до сих пор, был канал с аддитивным белым гауссовским шумом. В этой модели сигнал на выходе канала имеет вид
|
r(t) = s(t) + |
n(t) , |
(23.1) |
где s(t) {si (t)}iq=− |
01 переданный сигнал, |
принимающий значения из конечного |
|
сигнального множества, n(t) - белый гауссовский шум. Более сложный класс моделей каналов образуют каналы со случайными параметрами. В канале со случайными параметрами сигнал на выходе канала имеет вид
r(t) = s(t, a) + n(t) , |
(23.2) |
где a - вектор параметров сигнала, случайно изменяемых при передаче по каналу, a = (a1 ,..., aL ) , L - число случайных параметров, n(t) - белый
гауссовский шум. Обычно случайные параметры и шум статистически независимы. При некотором значении вектора случайных параметров, скажем
при a = a0 , имеет место равенство s(t) = s(t, a0 ) где s(t) {si (t)}iq=−01 . Иначе
говоря, если значения параметров сигнала не меняются и равны a0 , то имеет
место канал с АБГШ. Канал со случайными параметрами задан, если задано распределение вектора случайных параметров a . Обычно предполагается, что значение вектора случайных параметров не известно или не точно известно в точке приема и приемник должен быть построен с учетом этого обстоятельства.
Иллюстрация приведена на рис. 23.1

s(t, a0 ) |
|
|
Случайное |
||
|
|
изменение |
|
|
|
|
|
параметров |
s(t, a) |
r(t) |
 +
+
n(t)
Рис. 23.1 Общая схема канала со случайными параметрами
Как правило, число случайных параметров невелико, например, в модели канала со случайной фазой рассматривается только один случайный параметр – фазовый сдвиг приходящего сигнала. При рассмотрении канала со случайной
фазой предполагается использование сигнала, передаваемого на одной несущей
частоте (или на одной из нескольких несущих). Рассмотрим для примера передачу с использованием ЧМ, то есть
si (t) = |
2E |
cos 2π fi t , 0 < t < T , i = 0,1,..., q − 1. |
|
|
T |
|
|
Сигнал на выходе канала со случайной фазой имеет вид |
|||
r(t) = |
2E |
cos(2π fi t − θ ) + n(t) , |
|
|
|
T |
|
где θ - случайный фазовый сдвиг. |
Распределение случайного фазового сдвига |
||
может быть задано различным образом. Наиболее простым и распространенным является предположение о равномерном распределении фазового сдвига, то есть
плотность вероятностей величины θ |
|
задается как |
|
|||
|
|
1 |
, 0 ≤ θ |
< 2π |
|
|
w(θ ) = |
|
|
. |
|||
2π |
||||||
|
|
|
||||
|
|
0, иначе |
|
|
||
|
|
|
|
|||
Причины случайного фазового сдвига могут быть различными; в частности, он может возникать из-за условий распространения сигнала и/или из-за нестабильного формирования сигнала в передатчике.
24. Оптимальный прием дискретных сигналов в канале со случайной фазой
Рассмотрим равновероятную передачу ЧМ сигналов по каналу со
случайной фазой. Сигналы ЧМ имеют вид si (t) =  2E / T cos 2πfi t , 0 < t < T , i = 0,1,2,..., q −1. Частоты сигналов fi выбираются так, чтобы сигналы были
2E / T cos 2πfi t , 0 < t < T , i = 0,1,2,..., q −1. Частоты сигналов fi выбираются так, чтобы сигналы были
ортогональны в усиленном смысле. Ортогональность в усиленном смысле означает, выполнение следующих условий
T |
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
1, i |
= k |
|
∫ |
2 / T cos 2πfi t |
2 / T cos 2πfk tdt = ∫ |
|
|
|
|
|
|
|||||||||
2 / T sin 2πfi t 2 / T sin 2πfk tdt = |
|
||||||||||||||||
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0, i ≠ k |
||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ 2 / T cos 2πfi t |
2 / T sin 2πfk tdt = 0 . |
|
|
|
|||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Это условие достигается если |
|
fi = f0 |
+ i∆ f , где f0 |
= l0 / T , l0 целое, и ∆ f |
= l / T , |
||||||||||||
l - целое. Минимальный |
шаг по частоте, при |
|
котором |
достигается |
|||||||||||||
ортогональность в усиленном смысле, равен 1/ T . Заметим, что ортогональность |
|||||||||||||||||
в обычном смысле означает лишь, что |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
T |
|
|
|
|
|
|
|
|
1, i = k |
|
|
|
||
|
|
|
∫ |
2 / T cos 2πfi t |
2 / T cos 2πfk tdt |
|
|
|
|||||||||
|
|
|
= |
|
|
|
|
|
|||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
0, i ≠ k |
|
|
|
||
и достигается ∆ f |
= l / 2T , l - целое. |
|
|
|
|
|
|
|
|
|
|
||||||
|
Упражнение. Покажите, что |
|
|
|
|
|
|
|
|
|
|
||||||
T |
|
i |
|
|
|
2π |
k |
|
|
|
|
|
|
|
|
|
|
а) ∫ |
2 / T cos 2π |
T |
t |
2 / T sin |
T |
t dt = |
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 − cos 4πk |
, i = k |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4πk |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
= |
(i + k) cos 2π(i − k) − (i − k) cos 2π(i + k) − 2k , |
i ≠ k |
|||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2π(i |
2 |
− k |
2 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||

б) |
T |
|
i |
|
|
2π |
k |
|
sin 2π(i + k) |
+ |
sin 2π(i − k) |
, |
||||
∫ |
2 / T cos 2π |
T |
t |
2 / T cos |
T |
t dt = |
2π(i + k) |
|
2π(i − k) |
|
||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||
в) |
T |
|
i |
|
|
|
|
k |
|
sin 2π(i − k) |
− |
sin 2π(i + k) |
. |
|
||
∫ |
2 / T sin 2π |
T |
t |
2 / T sin 2π |
T |
t dt = |
2π(i − k) |
|
2π(i + k) |
|
||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||
Сигнал на выходе канала со случайной фазой имеет вид
|
|
r(t) = 2E / T cos(2πfi t −θ) + n(t) , |
|
(24.1) |
|||||||
где θ - случайный фазовый сдвиг, n(t) - белый гауссовский |
шум. |
С |
|||||||||
использованием тождества |
cos(x − y) = cos x cos y +sin x sin y , равенство (24.1) |
||||||||||
можно представить в виде |
|
|
|
|
|
|
|
|
|
||
r(t) = ( |
E cosθ) 2 / T cos 2πfi t + ( |
E sinθ) 2 / T sin 2πfi t + n(t) . |
(24.2) |
||||||||
Функции |
2 / T cos 2πfi t |
и |
2 / T sin 2πfi t , |
i = 0,1,2..., q −1, |
образуют |
||||||
ортонормированный |
базис, состоящий из 2q функций. Обозначим скалярные |
||||||||||
произведения |
принятого |
сигнала и |
косинуса |
и |
синуса |
i -й |
частоты, |
||||
i = 0,1,..., q −1, |
как |
rci |
и |
rsi , |
то |
есть |
rci |
= ∫0T r(t) |
2 / T cos 2πfi tdt , |
||
rsi = ∫0T r(t) 2 / T sin 2πfi tdt . |
Аналогично, |
скалярные |
произведения |
шума |
и |
||||||
косинуса и синуса i -й частоты обозначим как nci |
и nsi . Далее введем векторы |
||||||||||
rc = (rc0 ,..., rcq−1 ) , rs |
= (rs0 ,..., rsq−1 ) |
и |
nc |
= (nc0 ,..., ncq−1 ) , n s = (ns0 ,..., nsq−1 ) , |
а |
||||||
также r = (rc , rs ) , |
n = (nc , n s ) . |
Тогда |
для принятого сигнала (24.2) можно |
||||||||
получить векторное представление |
|
|
|
|
|
|
|
|
|||
|
|
|
r = si (θ) + n , |
|
|
|
(24.3) |
||||
где все |
векторы имеют размерность 2q , а si (θ) = (si cosθ,si sinθ) и |
si = (si0 ,..., siq−1 ) , причем |
|
s = E , k = i, ki 0, k ≠ i
При получении представления (24.3) использовано свойство усиленной ортогональности сигналов.
Обозначим условную плотность вероятностей вектора r при условии передачи i -го сигнала как w(r | i) . Оптимальный приемник принимает решение
по правилу i = arg max w(r | i) . Рассмотрим выражение для плотности w(r | i) .
0≤i≤q−1
Ясно, что
2π |
2π |
|
w(r | i) = ∫w(r | i,θ)w(θ)dθ = (2π)−1 ∫w(r | i,θ)dθ , |
(24.4) |
|
0 |
0 |
|
где w(r | i,θ) - условная плотность вероятностей при фиксированном значении
случайной фазы, w(θ) - |
плотность |
вероятностей |
|
|
|
|
|
|
случайной |
фазы, |
||||||||||||||||||||||
w(θ) = (2π)−1 , 0 <θ < 2π . |
Для |
условной плотности |
вероятностей |
w(r | i,θ) |
||||||||||||||||||||||||||||
можно записать, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w(r | i,θ) = w(rc | i,θ)w(rs |
| i,θ) , |
|
|
|
|
|
|
|
|
|
|
|
(24.5) |
||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
q / 2 |
|
|
|
|
r |
−s |
|
cosθ |
|
|
|
|
|
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
w(rc |
| i,θ) = |
|
|
exp − |
|
|
|
c |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
, |
(24.6а) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
πN0 |
|
|
|
|
|
|
|
|
N0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
1 |
q / 2 |
|
|
|
|
r |
−s |
|
|
sinθ |
|
|
|
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
w(rs | i,θ) = |
|
|
|
|
|
|
|
|
s |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
(24.6б) |
||||||
|
|
exp − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
N0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
πN0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
После подстановки равенств (24.6) в (24.5) имеем
|
2(rc , si ) cosθ + 2(rs , si ) sinθ |
|
|
|
|
|
|
|
|
||
w(r | i,θ) = K (r) exp |
|
|
, |
(24.7) |
|
N0 |
|||||
|
|
|
|
|
|
1 |
q |
|
|
|
|
|
r |
|
|
|
2 + |
|
|
|
r |
|
|
|
2 + E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
s |
|
|
|
|
|
- величина, не зависящая от i и θ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
где |
K (r) == |
πN0 |
|
exp |
− |
|
|
|
|
|
|
|
N0 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Рассмотрим скалярные произведения в показателе экспоненты в (24.7). Они
равны |
(rc ,si ) = ∑kq=−10 rck sik = rci |
E |
|
и (rs , si ) = ∑kq=−10 rsk sik = rsi |
|
E . |
Поэтому |
||||||||||
показатель экспоненты в (24.7) может быть записан в виде |
|
|
|
|
|||||||||||||
|
|
|
2 |
E (r |
cosθ + r |
sinθ) , |
|
|
|
|
|
|
|||||
|
|
|
N0 |
ci |
|
si |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
или с использованием тождества |
a cos x +b sin x = |
|
|
a2 + b2 cos(x − arctan(b / a)) |
|||||||||||||
преобразован к виду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
E |
(r |
)2 |
+ (r )2 cos(θ −φ |
) , |
|
|
|
|
||||||
|
|
N0 |
ci |
|
|
si |
|
|
|
i |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где φi |
= arctan(rsi / rci ) . Тогда для плотности w(r | i,θ) |
имеем выражение |
|
||||||||||||||
|
|
|
|
|
2 |
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(r ) |
2 |
+ (r |
) |
2 |
cos(θ −φ |
) |
|
. |
|
|||
|
w(r | i,θ) = K (r) exp |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
N0 |
ci |
|
si |
|
|
i |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставляя это выражение в (24.4), получаем |
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
2π |
|
2 |
E |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
w(r | i) = K (r) |
|
|
(rci ) |
+ (rsi |
) |
cos(θ −φi |
|
|
|
|
||||||
|
2π |
∫exp |
N0 |
|
|
) dθ . |
|
||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||
Выражение вида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I0 (x) = |
1 |
|
2πexp(x cos(α − β))dα , |
|
|
|
|
|||||||||
|
2π |
|
|
|
|
||||||||||||
|
|
|
|
∫0 |
|
|
|
|
|
|
|
|
|
|
|
||
где β - любое, известно как функция Бесселя первого рода нулевого порядка. График функции I0 (x) показан на рис.24.1
Рис.24.1 График функцииI0 (x)
С использованием определения функции I0 ( ) имеем
w(r | i) = K (r)I0 ((2 E / N0 )
E / N0 )  (rci )2 + (rsi )2 ).
(rci )2 + (rsi )2 ).
Оптимальное решение строится по правилу
i = arg max w(r | i) .
0≤i≤q−1
Поскольку функция квадратного корня и функция Бесселя монотонно возрастают, то эквивалентное правило принятия решения имеет вид
i = arg max ((rci )2 + (rsi )2 ).
0≤i≤q−1
Схема, реализующая это правило, показана на рис. 24.2.
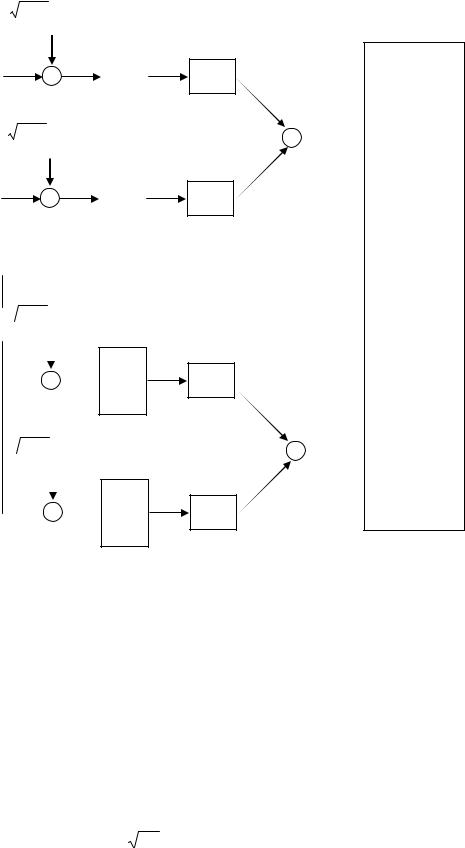
|
|
2 / T cos 2πf0t |
|
|
|
|
|
|
|
|
|
× |
|
T∫dt |
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
|
|
2 / T sin 2πf0t |
|
|
|
|
|
|
|
r(t) |
× |
|
T∫dt |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 2 / T cos 2πfq−1t
2 / T cos 2πfq−1t
 ×
×  T∫dt
T∫dt
0
 2 / T sin 2πfq−1t
2 / T sin 2πfq−1t
 ×
×  T∫dt
T∫dt
0
( )2
+ 
( )2
Выбор i максимума 
( )2
+ 
( )2
Рис.24.2 Схема оптимального приемника ЧМ сигналов в канале со случайной фазой
Рассмотрим теперь кратко другой метод передачи сигналов по каналу со случайной фазой – передачу с использованием сигналов с ортогональными огибающими. В этом случае сигналы передаются на одной несущей частоте и
имеют вид si (t) = mi (t) 2E cos 2πf0t , где |
mi (t) - ортонормированные на |
интервале [0,T ] огибающие, i = 0,1,..., q −1. В качестве огибающих могут быть использованы любые ортонормированные функции. Важно только чтобы они
были низкочастотными по сравнению со значением несущей частоты f0 . Часто
в качестве огибающих используются кусочно-постоянные функции, полученные с использованием кода Адамара1 соответствующего порядка. Например, для q = 8 огибающие показаны на рис.24.3.
Рис.24.3 Ортогональные огибающие, построенные на основе кода Адамара, q = 8 .
Огибающие, построенные с использованием кода Адамара, состоят из q
элементов сигнала, или чипов (chip), длительности Tc = T / q .
1 Код Адамара определяется как набор векторов, совпадающих со строками матрицы Адамара.
Матрица Адамара |
|
порядка |
|
n = 2k |
может быть определена рекурсивно |
|||
H |
n / 2 |
H |
n / 2 |
|
|
H 2 |
1 |
1 |
как H n = |
|
|
, и |
= |
. |
|||
H n / 2 |
− H n / 2 |
|
|
1 |
−1 |
|||
Условие низкочастотности огибающей, упомянутое выше, состоит в данном случае в том, что f0 >>1/ Tc , то есть на длительности чипа должно
помещаться много периодов несущей.
Принятый сигнал в отсутствие шума имеет вид
r(t) = mi (t) 2E cos(2πf0t −θ) = mi (t)
2E cos(2πf0t −θ) = mi (t)  2E (cosθ cos 2πf0t + sinθ sin 2πf0t) .
2E (cosθ cos 2πf0t + sinθ sin 2πf0t) .
В приемнике сначала выполняется низкочастотная демодуляция (перенос спектра в низкочастотную область). Эта операция выполняется следующим
образом. Сначала принятый сигнал умножается на 2 cos 2πf0t и |
2 sin 2πf0t и |
||
потом пропускается через |
фильтр низких частот, |
то есть |
вычисляются |
rc (t) = (r(t) 2 cos 2πf0t)НЧ и |
rs (t) = (r(t) 2 sin 2πf0t)НЧ . |
Здесь |
через ( )НЧ |
обозначена операция низкочастотной фильтрации выражения, стоящего в скобках. Рассмотрим вычисление rc (t) ,
rc (t) = (r(t) 2 cos 2πf0t)НЧ =
2 cos 2πf0t)НЧ =  2E
2E  2(mi (t) cos(2πf0 t −θ) cos 2πf0t)НЧ =
2(mi (t) cos(2πf0 t −θ) cos 2πf0t)НЧ =
=2 E (mi (t) cosθ cos 2πf0t cos 2πf0 t + sinθ sin 2πf0t cos 2πf0t)НЧ =
E (mi (t) cosθ cos 2πf0t cos 2πf0 t + sinθ sin 2πf0t cos 2πf0t)НЧ =
Поскольку
=cos2 x = (1 + cos 2x) / 2 =  E (mi (t)(cosθ(1 + cos 4πf0t) +sinθ sin 4πf0t))НЧ = cos x sin x = sin 2x / 2
E (mi (t)(cosθ(1 + cos 4πf0t) +sinθ sin 4πf0t))НЧ = cos x sin x = sin 2x / 2
= Emi (t) cosθ .
Emi (t) cosθ .
При переходе к последнему выражению учтено, что НЧ фильтр полностью подавляет составляющие удвоенной частоты. Аналогично можно показать, что
rs (t) =  Emi (t) sinθ .
Emi (t) sinθ .
Далее в приемнике вычисляются скалярные произведения функций rc (t)
и rs (t) и ортогональных огибающих, возведение в квадрат, сложение и
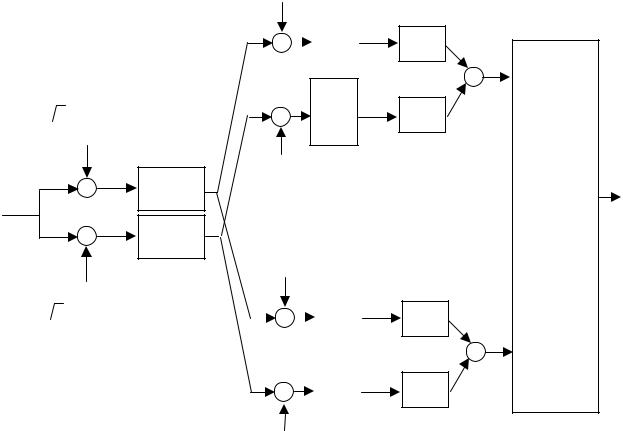
окончательного решения. Схема некогерентного приемника для сигналов с ортогональными огибающими показана на рис.24.4.
 2 cos 2!f0 t
2 cos 2!f0 t
r(t) |
НЧ |
|
< |
||
фильтр |
||
|
||
< |
НЧ |
|
фильтр |
||
|
 2 sin 2!f0 t
2 sin 2!f0 t
m0 (t) |
|
||
T |
|||
< |
|
|
%dt |
|
|
||
|
|
|
0 |
|
|
|
|
T
<%dt
0
m0 (t)
mq 1 (t)
|
|
|
|
|
|
T |
|
|
< |
|
|
|
%dt |
|
|
|
|
|||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
< |
|
|
|
%dt |
||
|
|
|
|
|
|
0 |
mq 1 (t) |
|
|
||||
|
|
|||||
(;)2
+
(;)2
!
i
Выбор
максимума
(;)2
+
(;)2
Рис.24.4 Схема некогерентного приемника для сигналов с ортогональными огибающими.
