Senikov_POE 3к

При заполнении матрицы планирования значения уровней факторов, в целях упрощения, обозначают соответствующими знаками, а цифру 1 опускают. С учетом взаимодействия факторов х1 и х2 таблицу 5.1 можно переписать следующим образом:

Таблица 5.2. Матрица планирования эксперимента с учетом взаимодействий

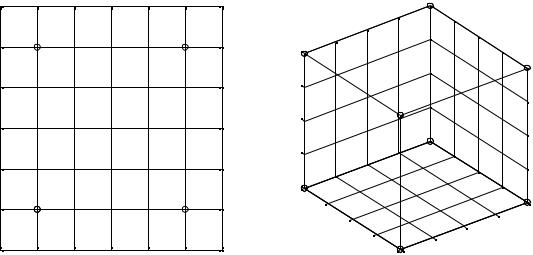
Каждый столбец в матрице планирования называют вектор-столбцом, а каждую строку – вектор-строкой. Таким образом, в таблице 5.2 мы имеем два векторастолбца независимых переменных и один вектор-столбец параметра оптимизации. То, что записано в алгебраической форме, можно изобразить графически. В области определения факторов находится точка, соответствующая основному уровню, и проводят через нее новые оси координат, параллельные осям натуральных значений факторов. Далее выбирают масштабы по новым осям так, чтобы интервал варьирования для каждого фактора равнялся единице. Тогда условия проведения опытов будут соответствовать вершинам квадрата, при k=2, и вершинам куба, при k=3. Центрами этих фигур является основной уровень, а каждая сторона равна двум интервалам (см. рис.5.1). Номера вершин квадрата и куба соответствуют номерам опытов в матрице планирования. Площадь, ограниченная этими фигурами, называется областью эксперимента. По аналогичному принципу располагаются экспериментальные точки при k>3.

21

нии линейных моделей. При этом нужно стремиться к тому, чтобы матрица планирования не лишилась своих оптимальных свойств. Сделать это не так просто, но все же возможно. Рассмотрим пути минимизации числа опытов.

5.6. Минимизация числа опытов

Еще раз рассмотрим матрицу планирования типа 22 (см. табл.5.3).

Таблица 5.3. Матрица планирования типа 22

Пользуясь таким планированием, можно вычислить четыре коэффициента и представить результаты эксперимента в виде неполного квадратного уравнения

y=a0+a1x1+a2x2+a12x1x2.

Если имеются основания считать, что в выбранных интервалах варьирования процесс может быть описан линейной моделью, то достаточно определить три коэффициента: a0, a1, a2. Остается одна степень свободы. Употребим ее для минимизации числа опытов. При линейном приближении a12 → 0 и вектор-столбец x1x2 можно использовать для нового фактора x3. Поставим этот фактор в скобках над взаимодействием x1x2 и посмотрим, каковы будут оценки коэффициентов. Здесь уже не будет тех раздельных оценок, которые были в полном факторном эксперименте. Оценки смешиваются следующим образом:

a1 → α1 + α23; a2 → α2 + α13; a3 → α3 + α12.

Если постулируются линейная модель, следовательно, все парные взаимодействия незначимы. Главное, найдено средство минимизации числа опытов: вместо восьми опытов для изучения трех факторов оказывается можно поставить четыре! При этом матрица планирования не теряет своих оптимальных свойств (ортогональность, ротатабельность и т.п.). Найденное правило можно сформулировать: чтобы сократить число опытов, нужно новому фактору присвоить вектор-столбец матрицы, принадлежащей взаимодействию, которым можно пренебречь. Тогда значения нового фактора в условиях опытов определяется знаками этого столбца. Мы рассмотрели самый простой случай. С увеличением числа факторов вопрос о минимизации опытов превращается в сложную задачу, и для определения ее требуется ввести новые определения и понятия: дробная реплика, генерирующее соотношение, определяющий контраст.

5.7. Дробная реплика

24

Поставив четыре опыта для оценки влияния трех факторов, мы воспользовались половиной факторного эксперимента 23, или «полурепликой». Если бы мы приравняли х3 к –х1х2, то получили бы вторую половину матрицы 23. В этом случае:

a1 → α1 - α23; a2 → α2 - α13; a3 → α3 - α12.

При реализации обеих полуреплик можно получить раздельные оценки для линейных коэффициентов (эффектов) и коэффициентов взаимодействия, как и в полном факторном эксперименте 23. Объединение этих двух полуреплик и есть полный факторный эксперимент 23. Матрица из восьми опытов для четырех факторного планирования будет полурепликой от полного факторного эксперимента 24, а для пятифакторного планирования – четвертьрепликой от 25. В последнем случае два линейных эффекта приравниваются к эффектам взаимодействия. Для обозначения дробных реплик, в которых L линейных эффектов приравнены к эффектам взаимодействия, удобно пользоваться условными обозначением 2(K-L). Так полуреплика от 26 запишется в виде 26-1, а четверть-реплика от 25 – в виде 25-2. Условные обозначения дробных реплик и количество опытов приведены в таблице 5.4.

Таблица 5.4. Условные обозначения дробных реплик и соответствующее число опытов

5.8. Выбор полуреплик. Генерирующие соотношения и определяющие контрасты

При построении полуреплик 23-1 существует две возможности: приравнять х3 к +х1х2 или к –х1х2. Поэтому есть только две полуреплики 23-1 (табл. 5.5).

25

помощью определения их уровней равными соответствующим членам взаимодействий. Например, рассмотрим следующий простой факторный план 3(3-1) (см. табл.6.1).

Таблица 6.1. Факторный план типа 3(3-1)

Как и в случае планов 2(K-L), план строится из полного факторного плана 3 – 1=2, чьи факторы перечислены в первых двух столбцах таблицы (факторы x1 и х2). Фактор х3 строится на основании взаимодействия х1х2 первых двух факторов. Значения фактора х3 вычисляются по формуле

х3 = 3 - mod3 (х1+х2),

где символ mod3(x) обозначает сравнение по модулю 3 (остаток от деления x

на 3).

Например, mod3(0)=0, mod3(1)=1, mod3(3)=0, mod3(5)=2 (3 – наибольшее число,

не большее 5, делящееся на 3; так что окончательно, 5-3=2) и так далее.

Если применить эту функцию к сумме столбцов х1 и х2 в таблице 6.1 можно получить третий столбец х3.

Анализ плана: см. раздел 6.4.

6.2. Планы Бокса-Бенкена

Эти планы конструируются комбинированием двухуровневых факторных планов с планами неполных блоков и имеют сложную смесь взаимодействий. Тем не менее, они экономичны, и, следовательно, особенно полезны в случаях, когда дорого проводить необходимые опыты. Исходные матрицы плана Бокса-Бенкена для 3-5 факторов приведены в Приложении 2.

Рассмотрим построение матрицы эксперимента для трех факторов (см.

табл.6.2).

Таблица 6.2. Исходная матрица (слева) и план эксперимента (справа) плана Бокса-Бенкена для трех факторов на трех уровнях

28

Анализ плана: см. раздел 6.4.

6.3. Планы для факторов на 2-х и 3-х уровнях

Если априорно известно линейное влияние одного или нескольких факторов на параметр оптимизации, то имеется возможность сократить количество экспериментов за счет использования смешанных планов на 2-х и 3-х уровнях. Эти планы очень эффективны, они не обязательно ортогональны [12].

План эксперимента 2K3M является комбинацией процедур, описанных для планов 2(K-P) и 3(K-P) (см. табл.6.3). Заполнение матрицы планирования начинается с факторов, находящихся на 3-х уровнях, а затем производится дополнение факторами, находящимися на 2-х уровнях.

Таблица 6.3. Примеры планов типа 2131 (слева) и 2231 (справа).

29

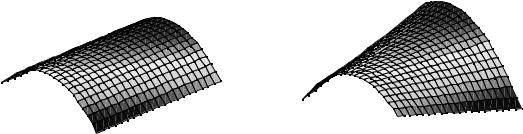
Рис.6.1. Виды поверхностей отклика для планов типа 2131 без взаимодействий (слева) и с взаимодействиями (справа).

Примеры получаемых регрессионных моделей:

y=a0+a1x1+a2x2+a22x22,

y=a0+a1x1+a2x2+a12x1x2+a33x32.

Для нахождения коэффициентов модели используется МНК для нелинейных моделей (см. раздел 6.4), который не требует ортогональности плана.

6.4. Метод наименьших квадратов для нелинейных моделей

Для линейных моделей вида (см. рис.4.1А,В) нахождение коэффициентов осуществляется достаточно по простым формулам (5.1-5.3). Наличие большого числа алгоритмов оптимизации и мощных вычислительных средств дает исследователю еще один, наиболее универсальный, способ нахождения коэффициентов, который заключается в «подгонке» заданной пользователем модели к экспериментальным данным.

Нахождение коэффициентов модели осуществляется с помощью ЭВМ, используется программная реализация какого-либо алгоритма оптимизации. В настоящий момент существует большое количество видов и модификаций оптимизирующих алгоритмов, но разработчики программного обеспечения отдают предпочтения, как правило, градиентным алгоритмам, которые, несмотря на относительно высокую сложность реализации, обладают хорошей скоростью и точностью работы. Тем не менее, каких-либо принципиальных ограничений на применение других алгоритмов оптимизации не существует – главное, чтобы последние эффективно решали поставленную задачу.

Исходными данными для алгоритма являются:

план эксперимента,

предварительно обработанные измерения (удалены грубые и систематические ошибки, оценена воспроизводимость опытов),

желаемый вид модели (обычно со всеми факторами и взаимодействиями).

Задача нахождения коэффициентов модели с помощью алгоритмов оптимизации заключается в подборе таких коэффициентов модели, при которых расхожде-

30