2. Скорость точек плоской фигуры

Для сечения плоской фигуры точка А принята за полюс. Положение полюса определено радиусом-вектором ,проведённым из начала координат в точку А. Требуется установить связь скорости точки М тела с характеристиками плоского движения тела. Отрезок постоянной длины рассматривается как вектор, определяющий положение точки М относительно полюса А.

Запишем векторное равенство , где - радиус-вектор полюса А; - радиус-вектор, определяющий положение точки М относительно полюса А.

Вектор скорости точки М

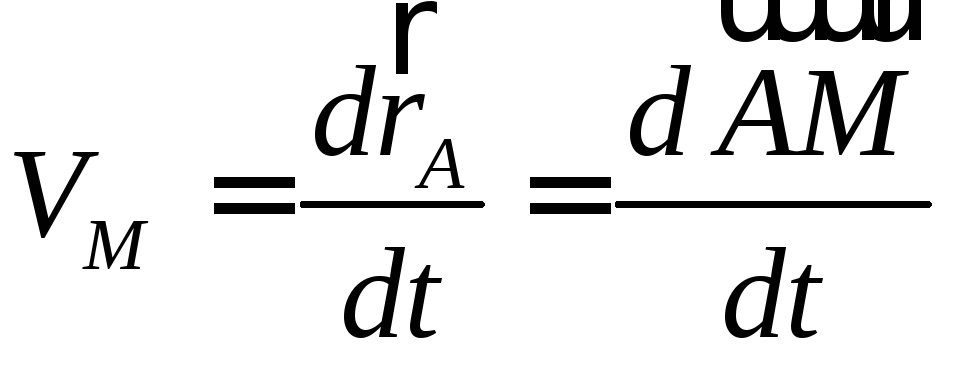или .

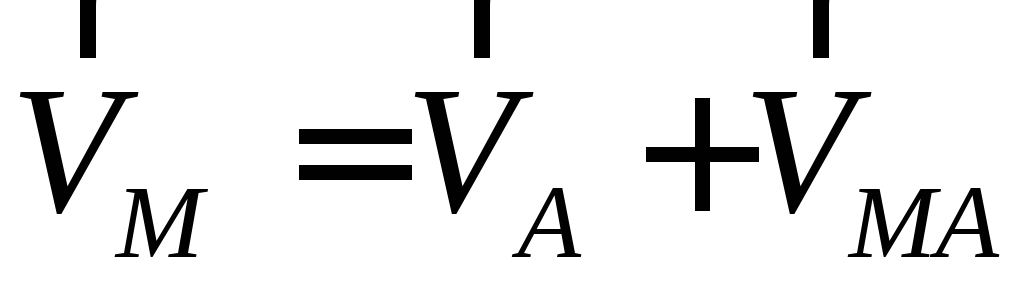В полученном уравнении -скорость точки М, которую она получает при вращении тела вокруг полюса А:

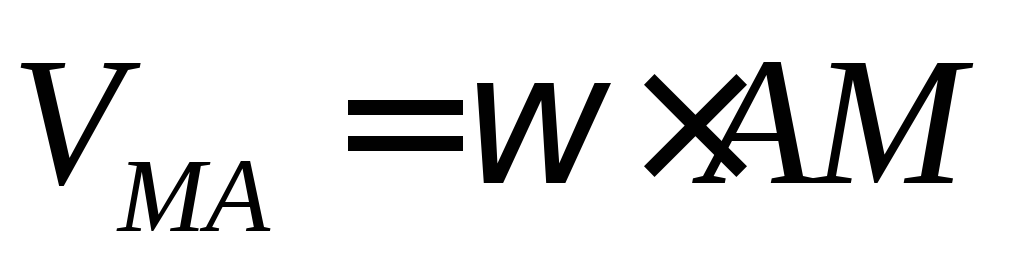или ,

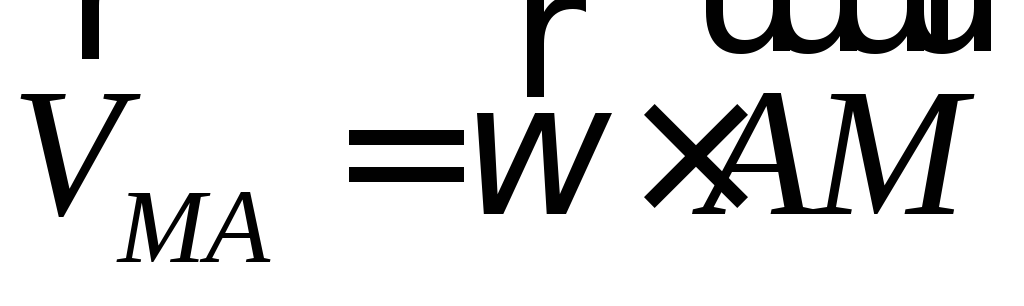где - угловая скорость вращения тела; - вектор угловой скорости тела.

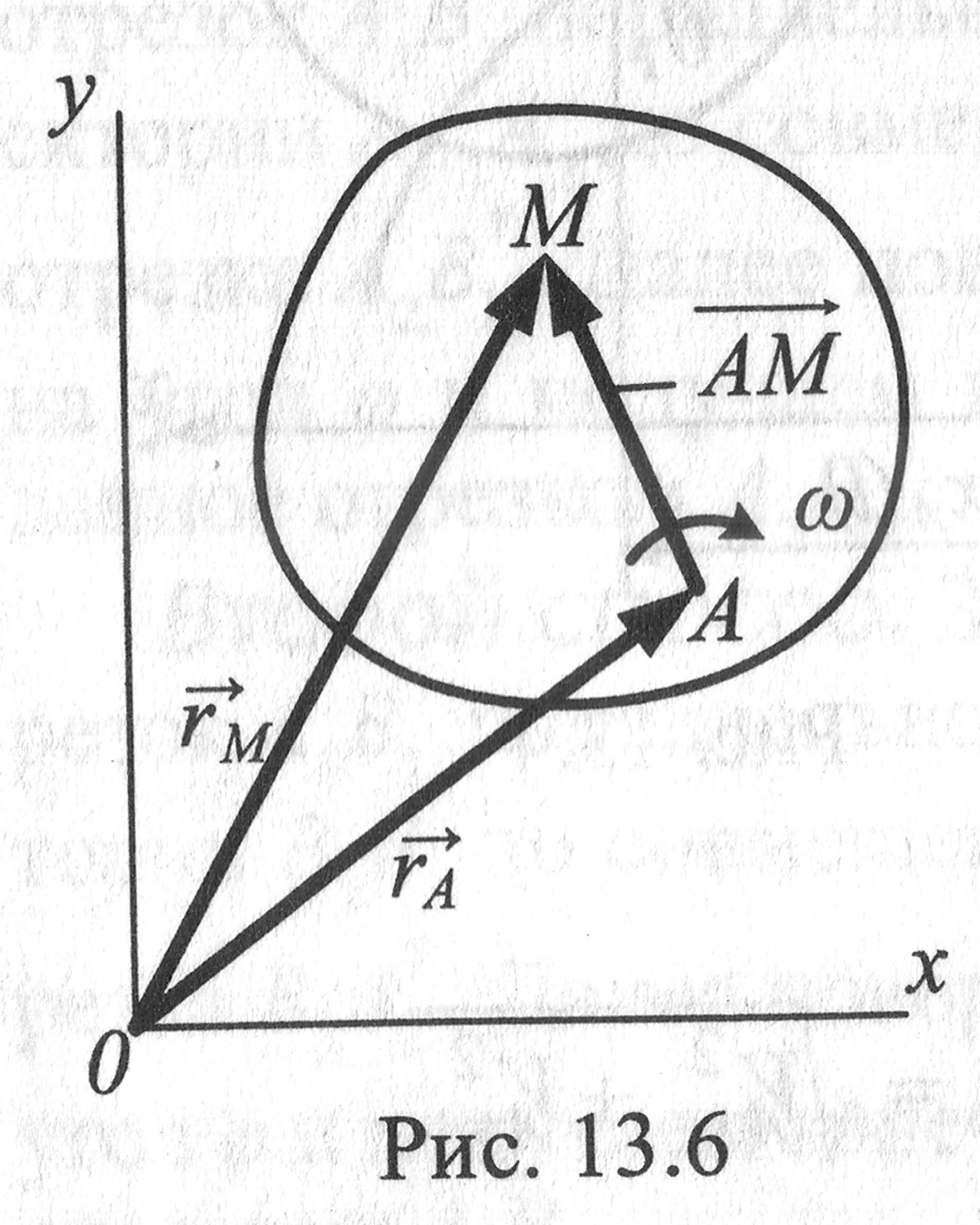
На рис. угловая скорость показана дуговой стрелкой, при этом вектор угловой скорости и перпендикулярен чертежу в точке А и направлен от нас. Таким образом, доказана теорема о сложении скоростей точки плоской фигуры.

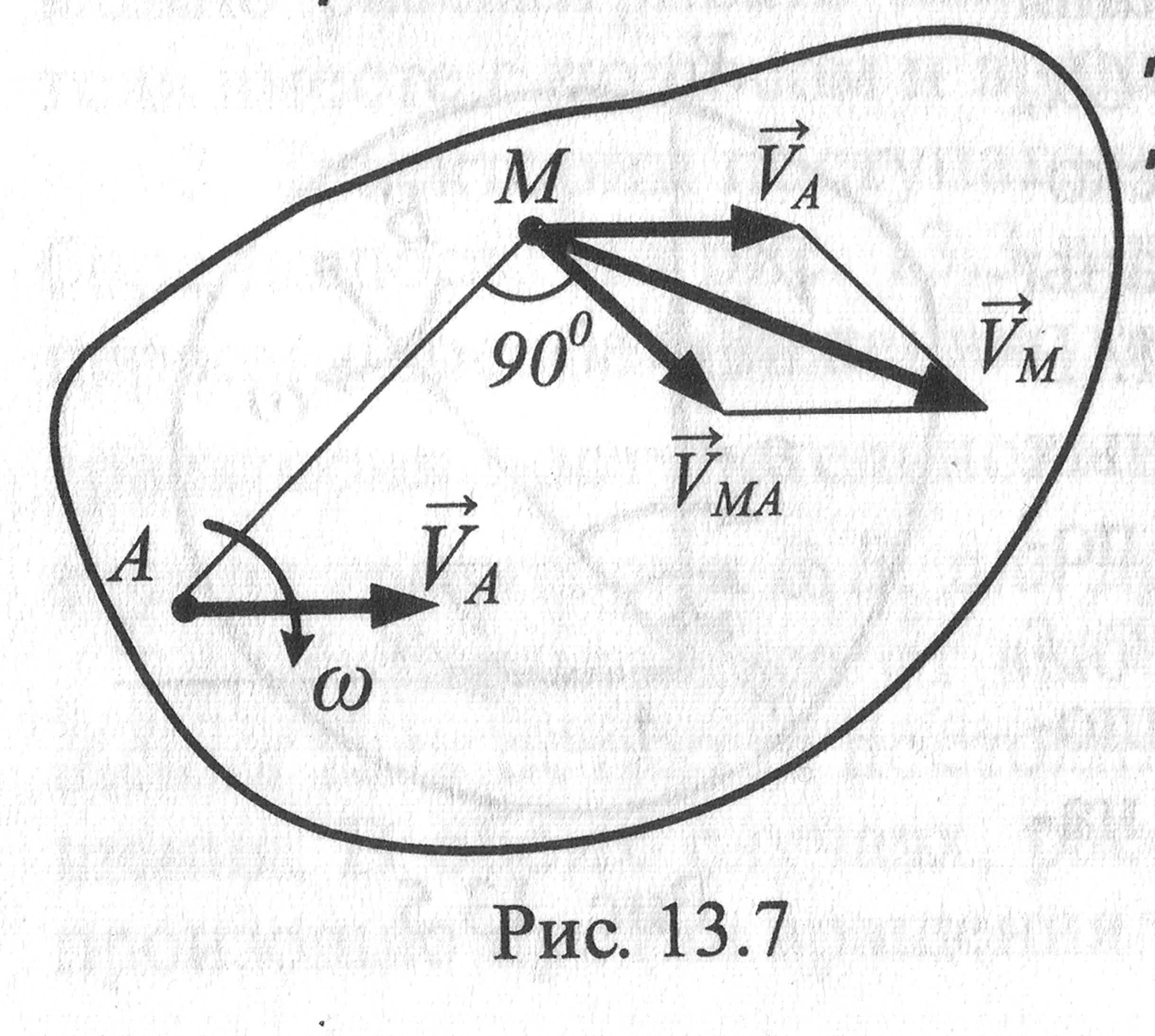
Теорема. Скорость любой точки М тела при плоском движении геометрически складывается из скорости полюса и скорости вращения точки М вокруг полюса.

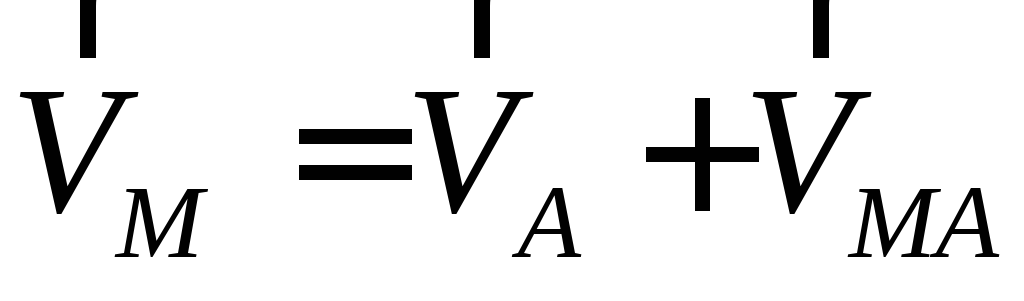
Направление скорости можно найти геометрическим построением параллелограмма векторов скоростей .

Полученная теорема для определения скоростей точек тела позволяет получить другие, практически более удобные и простые методы определения скоростей точек тела. Один из таких методов дает теорема о проекциях скоростей двух точек тела.

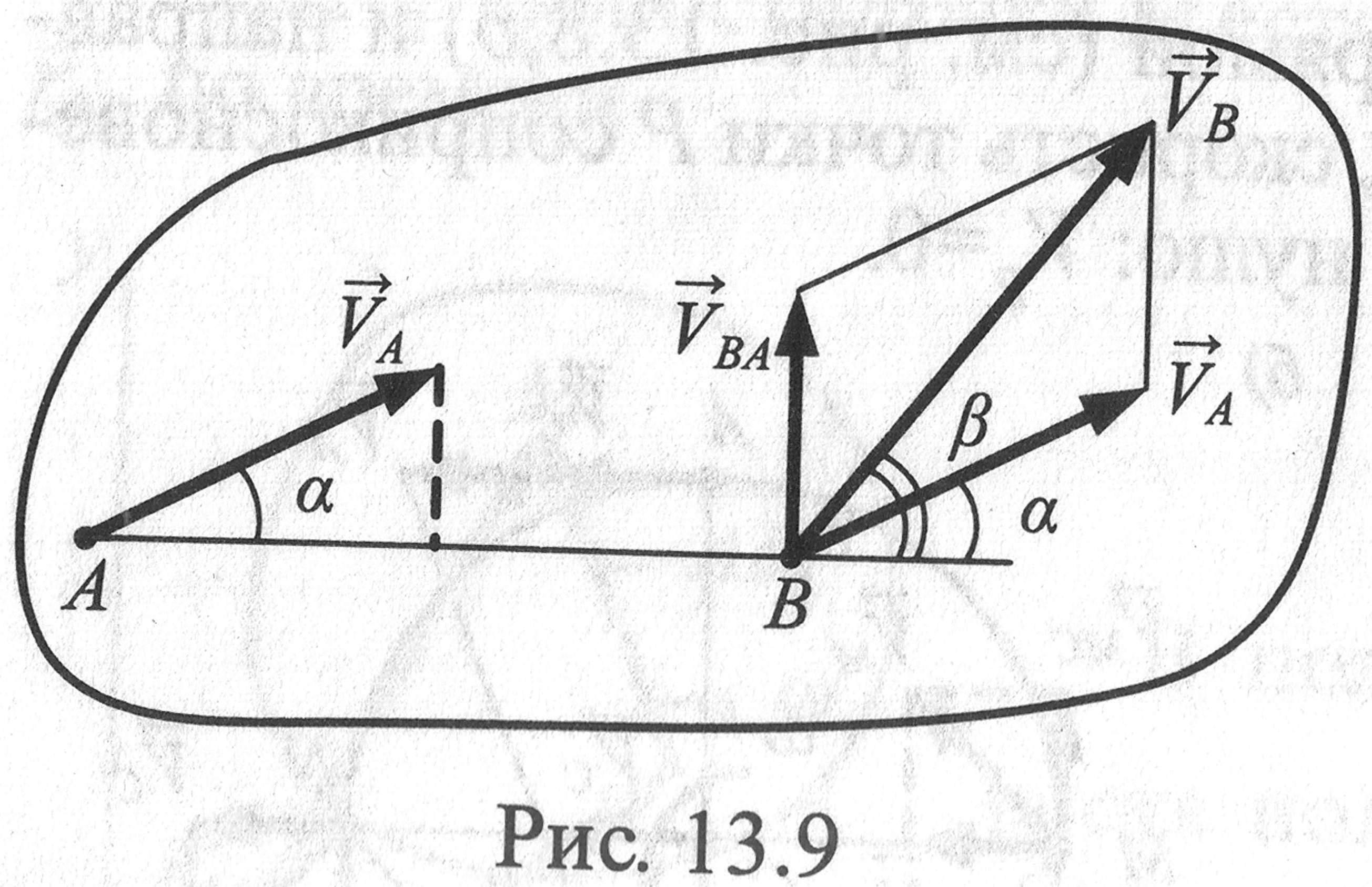
Теорема (следствие) 1. Проекции скоростей двух точек тела на прямую, соединяющею эти точки, всегда равны.

Рассмотрим две произвольные точки А и В тела . Принимая точку А за по-люс, получим . Отсюда, проецируя обе части равенства на линию АВ и учитывая, что вектор перпендикулярен к АВ, находим

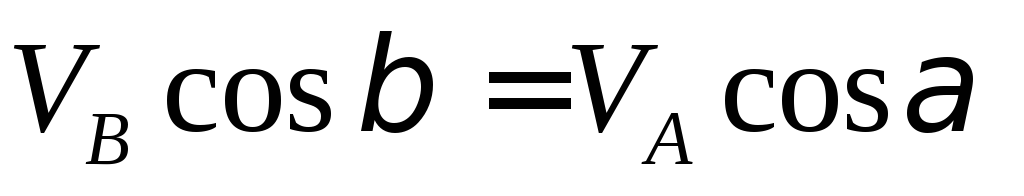
Эта теорема позволяет легко находить скорость данной точки тела, если известны направление движения этой точки и вектор скорости другой точки того же тела.

Теорема (следствие)2. Концы векторов скоростей точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные расстояниям между соответствующими точками отрезка.

Исходя из теоремы о скоростях точек при плоском движении тела, имеем

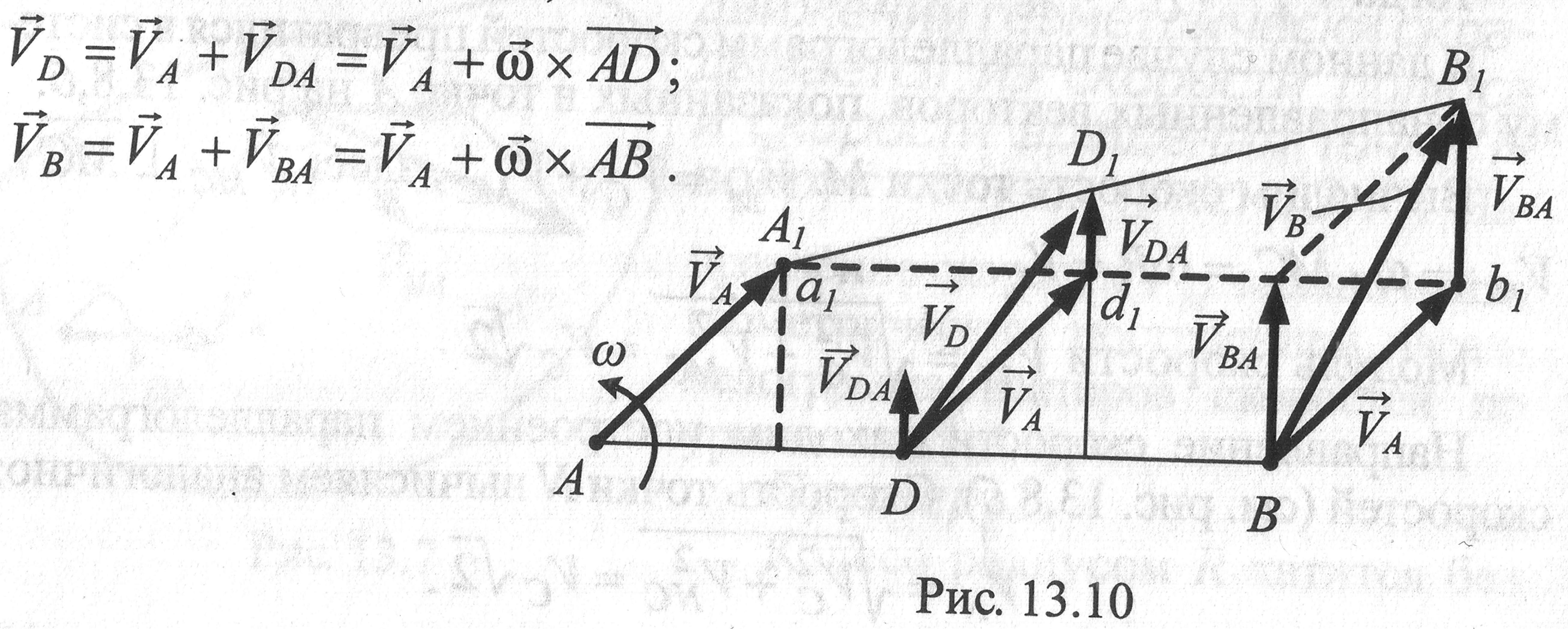
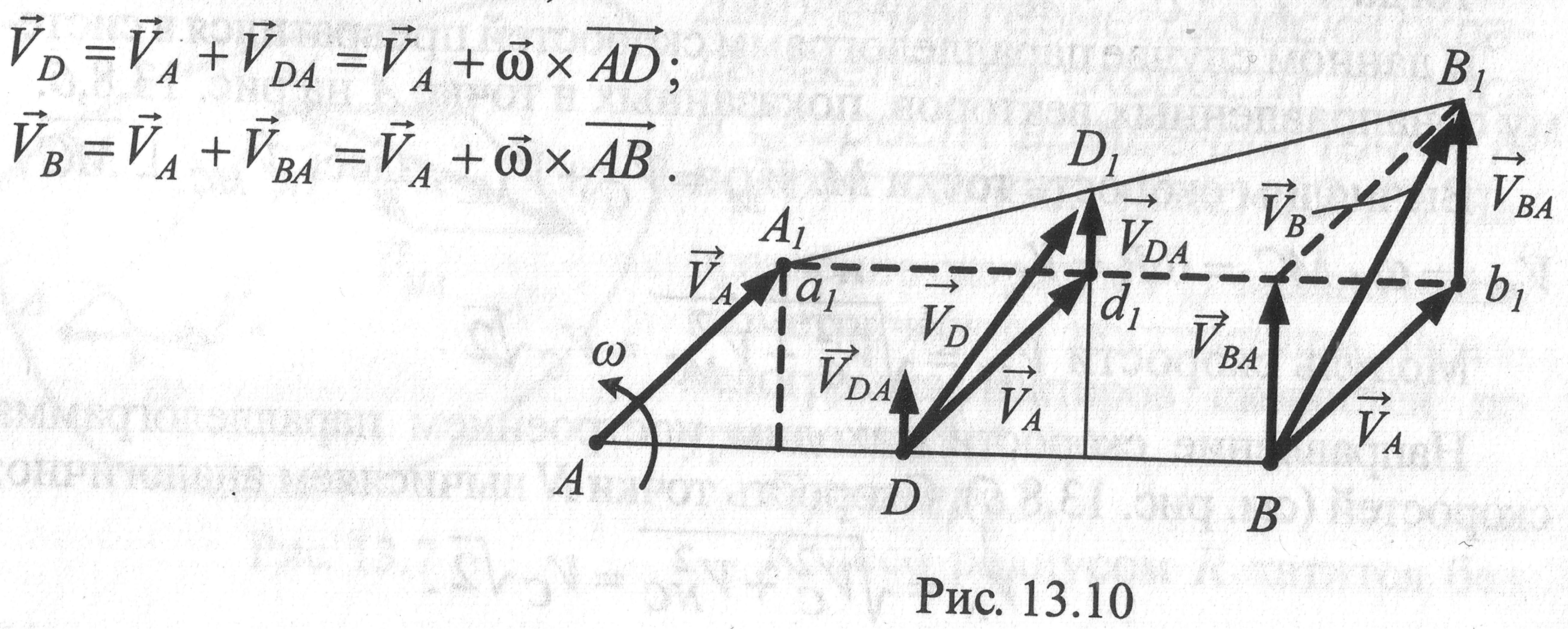
Тогда ии, следовательно,

или .

Т.к. и как противоположные стороны параллелограммов, то . Это соотношение показывает, что- отрезок прямой. Из подобияиимеем

или и,

т.е. расстояния между концами векторов скоростей пропорциональны расстояниям между соответствующими точками.

Задача 1. Для механизма, изображенного на рис., найти скорость точки В, если скорость точки А равна , угол.

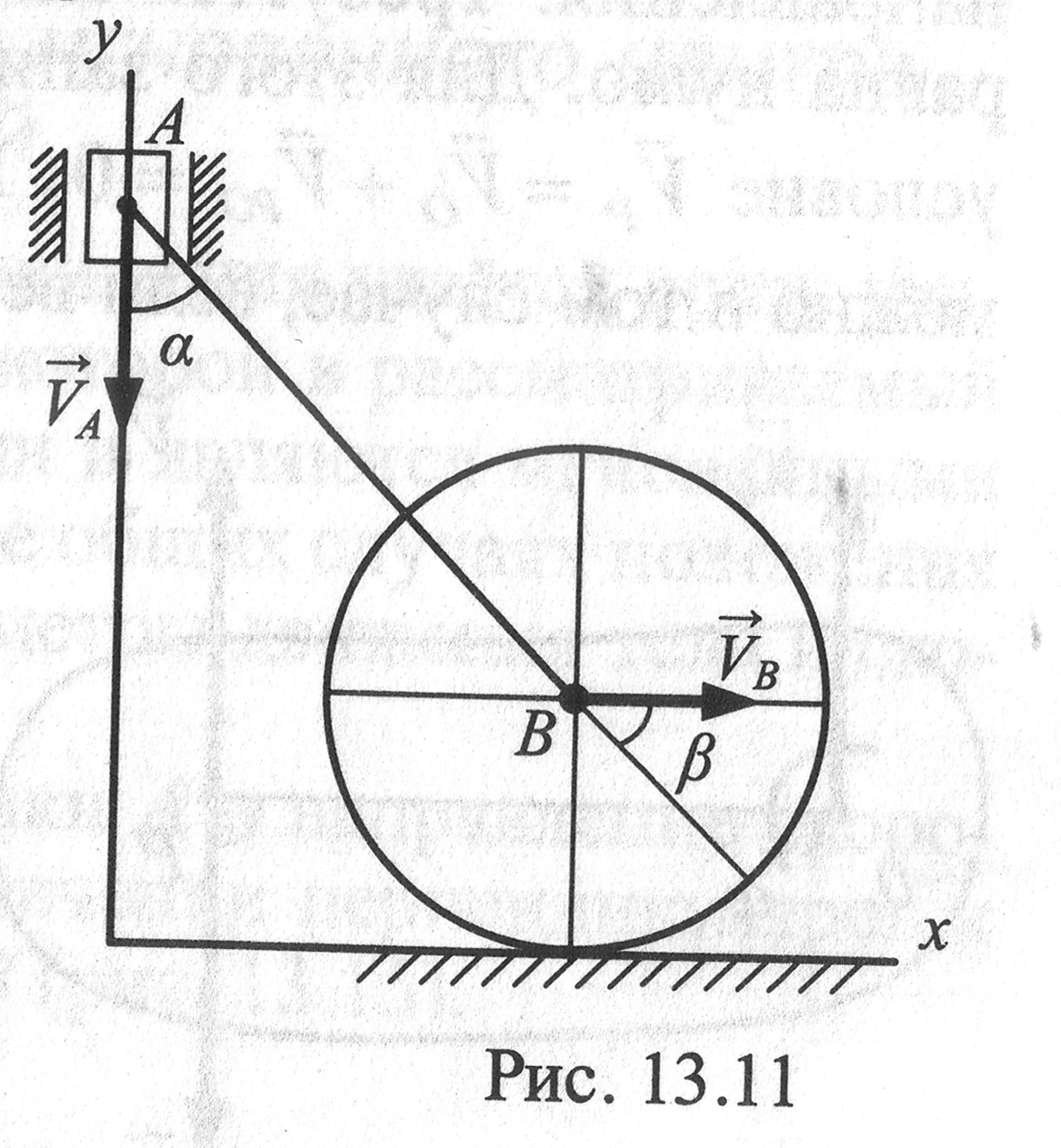
Решение. При движении ползуна А в направлении колесо катится вправо и точка В имеет скорость . Углы и образованы векторамии с прямой АВ. При ==45° _{, откуда} .

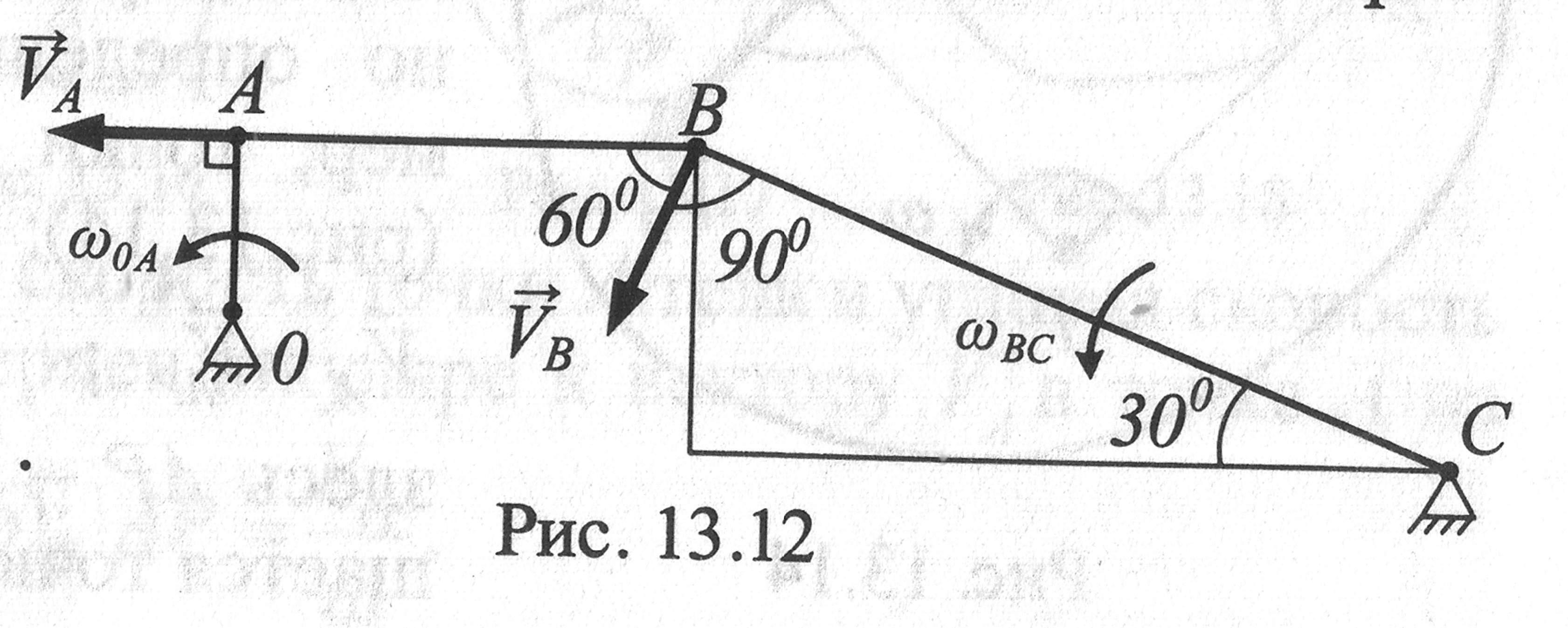
Задача 2. Кривошип ОА (рис. 13.12) длиной 1 м вращается с угловой скоростью = 2рад/с. Определить скорость точки В.

Решение. При заданном направлении вращения кривошипа ОА его скорость будет определяться вектором .Величина скорости =м/с.

Кривошип ВС при этом будет вращаться вокруг точки С угловой скоростью , и скорость точки В определится вектором .

, откуда м/с.