3.Теорема об изменении количества движения механической системы

Количество движения материальной точки — векторная мера ее движения, равная произведению массы точки на вектор ее скорости

.

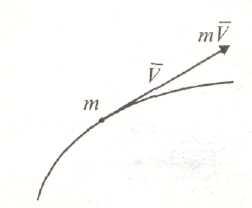
Количество движения механической системы или главный вектор количества движения — геометрическая сумма коли­честв движения всех материальных точек системы

.

,

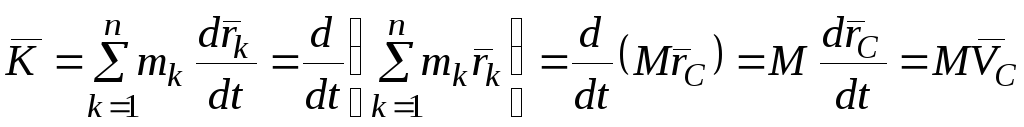где — скорость центра масс.

Если механическая система состоит из твердых тел, то по формуле определяется количество движения каждого k - гo тела, а затем

.

где — скорость центра масс k-то тела.

Модуль главного вектора количества движения системы оп­ределяется через его проекции на оси декартовых координат

.

Импульс силы — векторная мера действия силы в течение некоторого времени.

Элементарный импульс силы — векторная величина, равная произведению вектора силы на элементарный про­межуток времени

.

Импульс силы за конечный промежуток времени t ра­вен интегральной сумме соответствующих элементарных им­пульсов, т. е.

.

Выражение в проекциях на оси декартовых координат

.

Если на точку действует несколько сил, то они заменяются равнодействующей , импульс которой равен геометриче­ской сумме импульсов всех сил. Поясним это:

.

.

Действие внешних сил, приложенных к механической сис­теме за некоторый промежуток времени , характеризуется импульсом главного вектора внешних сил:

.

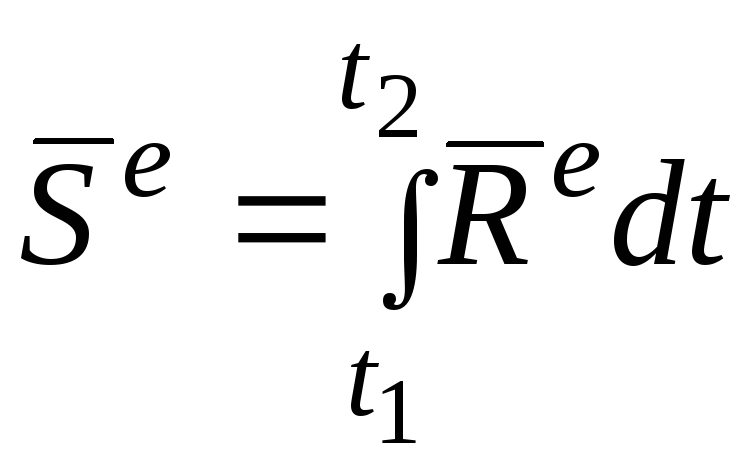Теорема об изменении количества движения материальной точки в дифференциальной форме. Производная по времени от количества движения мате­риальной точки равна геометрической сумме сил, дейст­вующих на точку

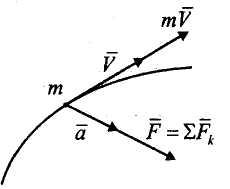
Доказательство. Запишем основ­ной закон динамики в виде

.

Теорема в интегральной (конечной) форме. Изменение количества движения материальной точки за некоторый промежуток времени равно геометрической сум­ме импульсов сил, действующих на точку, за тот же проме­жуток времени.

Доказательство.

.

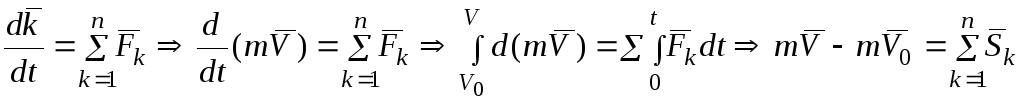Векторные равенства можно записать в про­екциях на оси декартовых координат:

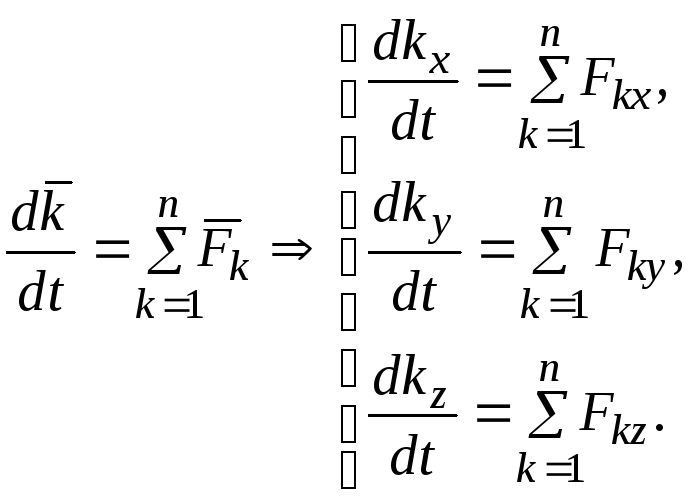
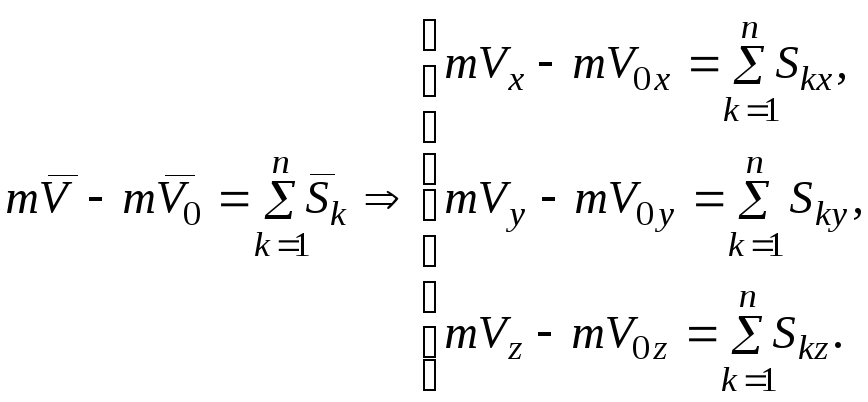
Задача 3. Точка массы т = 2 кг движется горизонтально под действи­ем силы Q = 20 Н в среде, сопротивление которой определяет­ся силой R = aV, где а = 0,4 кг/с. Какую скорость приобретет точка за время t = 10 с, если движение началось без начальной скорости?

Решение. Применим теорему об изменении материальной точки в дифференциальной форме в проекции на ось х. Покажем силы .

.

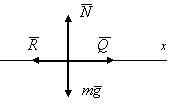
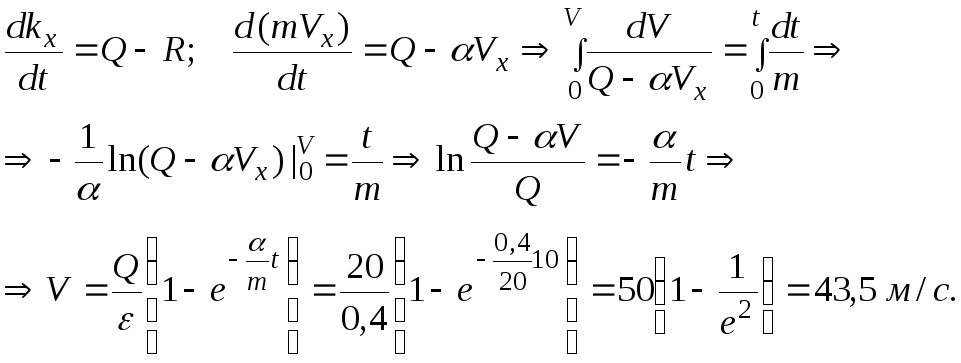
Задача 4. Материальная точка массы т = 1 кг движется по окружно­сти с постоянной скоростью V= 10 м/с из точки . Определить импульс сил, действую­щих на точку, за время, в течение которого точка пройдет длины окружности.

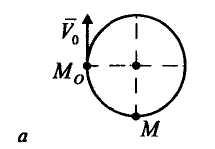
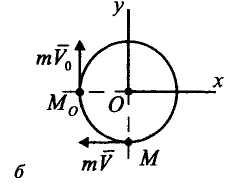
Решение. Применим теорему об из­менении количества движения мате­риальной точки в интегральной форме

.

Найдем проекции импульса на оси координат ху:

Импульс сил

.

Теорема об изменении главного вектора количества движения

механической системы в дифференциальной форме. Производная по времени от главного вектора количеств движения механической системы равна геометрической сумме внешних сил, действующих на эту систему.

Доказательство. На любую k - ю точку механической систе­мы действуют силы и . Для этой точки

.

Для всей системы

,

где

.

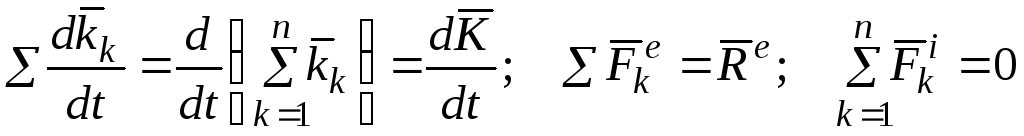В проекциях на оси декартовых координат имеет вид

. (4.22)

Следствия из теоремы:

1. Если , то .

2. Если проекция главного вектора на какую-либо ось равна нулю, то проекция количества движения на эту ось есть величина постоянная. Например, , то .

Теорема в интегральной (конечной) форме. Изменение количества движения механической системы за некоторый промежуток времени равно геометрической сумме импульсов всех внешних сил, действующих на точки механической системы, за тот же промежуток времени.

Доказательство.

.

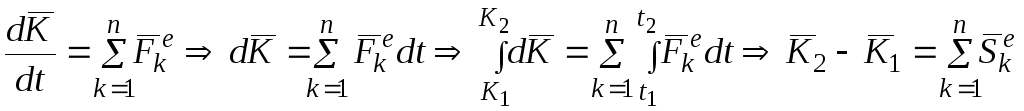где 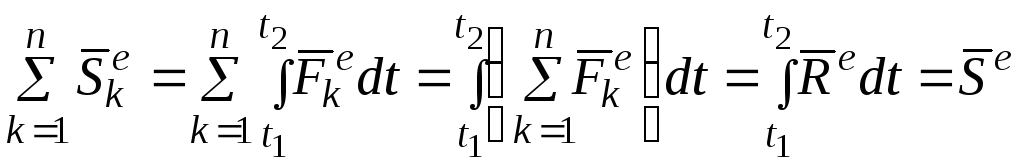- импульс главного вектора внешних сил.

Векторному равенству соответствуют три равенства в скалярной форме

.

Следствия из теоремы.

1. Если , то .

2. Если , то .

Задача 5.. Лодка массы М = 200 кг, на корме которой стоял человек массы т = 80 кг, двигалась со скоростью м/с. Затем че­ловек спрыгнул с лодки со скоростью u = 4 м/с против ее дви­жения. С какой скоростью V после этого будет двигаться лодка?

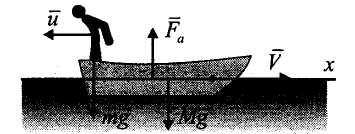
Решение. Внешними силами являются вес лодки , вес человека и выталкивающая сила . Силой сопро­тивления движению пренебрегаем. Все силы перпендикулярны оси х. Поэтому

.

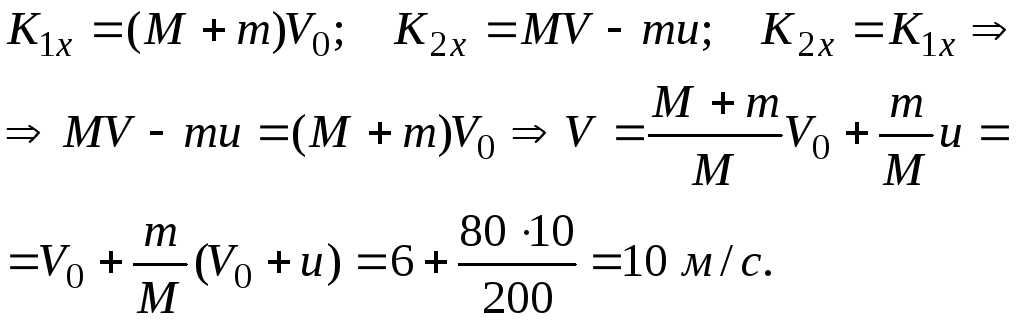
Базовые вопросы

1. Свойства внутренних сил.

2. Что называется а) центром масс механической системы, б) количеством движения точки и механической системы, в) импульсом силы.

3. Что представляют собой дифференциальные уравнения механической системы?

4. Сформулируйте теорему о движении центра масс механической системы.

5. Сущность следствий из теоремы о движения центра масс механической системы.

6. Поясните практическое применение теоремы о движении центра масс механической системы.

7. Сформулируйте теорему об изменении количества точки в дифференциальной и конечной формах.

8. Сформулируйте теорему об изменении количества механической системы в дифференциальной и конечной формах.

22