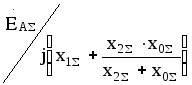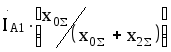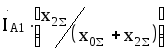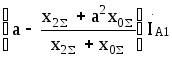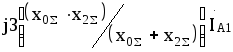8.5. Правило эквивалентности прямой последовательности

Из полученных в предыдущих разделах формул для различных видов несимметричных КЗ составим таблицу и проанализируем ее данные (табл. 8.1).

Из таблицы 8.1 видно, что токи обратной и нулевой последовательностей и напряжения всех последовательностей пропорциональны току прямой последовательности в месте КЗ . Таким образом, чтобы рассчитать любой вид КЗ, необходимо найти ток прямой последовательностив месте несимметричного КЗ.

Периодическую составляющую тока прямой последовательности любой фазы для любого (n) вида несимметричного КЗ можно выразить в общем виде:

, (8.40)

где х^{( n)}- дополнительное сопротивление, которое определяется для каждого вида КЗ:х⁽³⁾= 0;х⁽²⁾= х_2;х⁽¹⁾= х_2+ х_0;

х^(1,1)= х_0х_2(х_0+ х_2).

Обобщенная запись выражения (8.40) позволила отечественному ученому Н.Н. Щедрину впервые сформулировать так называемое правило эквивалентности прямой последовательности, которое используется электротехниками всех стран.

Вот его формулировка:

"Ток прямой последовательности любого несимметричного КЗ может быть определен как ток при трехфазном КЗ в точке, удаленной от действительной точки КЗ на дополнительное сопротивлениех⁽ⁿ⁾ , которое не зависит от параметров схемы прямой последовательности и для каждого вида КЗ определяется результирующими сопротивлениями обратной и нулевой последовательностей относительно рассматриваемой точки схемы..."2.

Из выражений для напряжения прямой последовательности, приведенных в табл. 8.1 можно записать в общем виде :

. (8.41)

"Установленная идентичность между током прямой последовательности несимметричного КЗ и током при некотором эквивалентном трехфазном КЗ указывает, что все полученные ранее выражения для тока трехфазного КЗ можно распространить на случаи несимметричных коротких замыканий"2.

Таблица 8.1

Симметричные составляющие токов и напряжений в месте кз

№	Определяемые величины	Вид несимметричного КЗ
п/п		К(2)	К(1)	К(1,1)
1	2	3	4	5
1	Периодическая составляющая тока прямой последовательности
2	Периодическая составляющая тока обратной последовательности	-		-
3	Периодическая составляющая тока нулевой последовательности	0		-
4	Напряжение прямой последовательности	jx2	j(x2 +x0)
5	Напряжение обратной последовательности	jx2	-jx2
6	Напряжение нулевой последовательности	—	-jx0

Окончание табл. 8.1

1	2	3	4	5
7	Периодические токи в фазах:	0 -j j	3 0 0	0
8	Фазные напряжения:	2jx2 -jx2 -jx2	0 j[(a2 - a)x2 + (a2 - 1) x0] j[(a - a2)x2 + (a - 1) x0]	0 0

Из табл. 8.1 также следует, что модуль фазного тока в месте КЗ можно определить по следующему общему выражению:

I⁽ⁿ⁾ = m⁽ⁿ⁾  I_A1⁽ⁿ⁾, (8.42)

где m⁽ⁿ⁾ - коэффициент, рассчитываемый для определенного вида КЗ:

m⁽³⁾= 1; m⁽²⁾=; m⁽¹⁾= 3;. (8.43)